算法试题——每日一练
删除排序链表中的重复元素
给定一个排序链表的头结点 h e a d head head,删除所有重复的元素,使每个元素只出现一次。并返回已排序的链表。
例如,给定一个序列[1,1,2],删除后返回[1,2]。又例如[1,1,2,2,3],删除后返回[1,2,3]。
思想:这个算法主要就是循环的条件,我们肯定是要从前往后遍历去找到重复的结点,那么这个循环在什么情况下结束,就很重要了。其次还要考虑该链表结点的情况,可能一个都没有,可能有一个,还可能有更多。
具体代码:
struct ListNode
{
int val;
struct ListNode *next;
};
struct ListNode* deleteDuplicates(struct ListNode* head)
{
struct ListNode *p,*q;
//如果该链表一个结点都没有的情况
if(!head)
return NULL;
//该链表只有一个结点的情况
else if(!head->next)
return head;
//该链表有两个以上结点的情况
else
{
p = head;
while(p->next) //循环结束条件
{
q = p->next; //注意这一行一定要放在循环的里面
if(p->val == q->val)
{
p->next = q->next;
}
else
p = q;
}
}
return head; //我们只是另设了两个指针用于删除重复的结点,head还是指向该链表的头结点
}
合并两个有序数组
给定两个递增排列的数组 n u m s 1 nums1 nums1, n u m s 2 nums2 nums2, m m m表示 n u m s 1 nums1 nums1中的元素个数, n n n表示 n u m s 2 nums2 nums2中元素的个数,请将 n u m s 2 nums2 nums2中的元素合并到 n u m s 1 nums1 nums1中,且合并后 n u m s 1 nums1 nums1中的元素仍按照递增的顺序排列。
其中, n u m s 1 nums1 nums1的数组大小为 n + m n+m n+m,后面 n n n个位置为0,应忽略。最好是设计一个算法时间复杂度为 O ( m + n ) O(m+n) O(m+n)。
思想:该题的主要思想就是如何避免多次循环去排序。一般情况下,我们都是从头开始比较,对于这样的题,比较后又要将其它元素像后移以便空出位置来,这样就太麻烦了。那么为什么不从尾开始比较试一试呢?如果我们从尾开始比较,并且 n u m s 1 nums1 nums1数组后面正好空出来了 n n n个位置,比较后,将较大的元素放在 n u m s 1 nums1 nums1的最后。不过比较也要看条件,循环结束的条件就是两个数组的下标有一个小于1。循环结束后,也不要忘了继续将另一个下标不为零的数组的元素赋值到 n u m s 1 nums1 nums1中去。
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n)
{
int i = m - 1,j = n - 1,k = m + n - 1;
while(j >= 0 && i >= 0)
{
if(nums2[j] >= nums1[i])
{
nums1[k--] = nums2[j--];
}
else
{
nums1[k--] = nums1[i--];
}
}
while(j >= 0)
{
nums1[k--] = nums2[j--];
}
while(i >= 0)
{
nums1[k--] = nums1[i--];
}
}
二叉树的中序遍历
一般面对二叉树的中序遍历,我们想到的都是递归,通过不断地调用函数实现。例如下面。
struct TreeNode
{
int val;
struct TreeNode *left;
struct TreeNode *right;
};
void inorder(struct TreeNode* root,int* a,int* returnSize)
{
if(!root)
return;
else
{
inorder(root->left,a,returnSize);
a[(*returnSize)++] = root->val;
inorder(root->right,a,returnSize);
}
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
*returnSize = 0;
//这里分配101个地址空间是因为规定了结点个数最多100个
int *t = (int *) malloc (sizeof(int) * 101);
inorder(root,t,returnSize);
return t;
}
但如果我们不用递归,用迭代的方式如何做到二叉树的中序遍历呢?力扣官方给出了两种解答。
首先,中序遍历二叉树就是要先遍历左子树、再遍历根结点、最后遍历中间结点,保持这样的顺序。那么我们就要先找到左子树最左的结点,然后它的根结点、根结点的右孩子…相当于是从最下面往上查找。那么这样也就明显了,可以利用栈先进后出的特性来做这个题(我就是没有想到这样就一直卡着,最后也是看的题解才知道)。那么我们只需要依次遍历根结点的左子树直到最左的那个结点,并在这个过程将指向每个结点的指针入栈,方便向上回溯的时候遍历它的右孩子。
struct TreeNode
{
int val;
struct TreeNode *left;
struct TreeNode *right;
};
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
//栈,用来记录一条路径上指向结点的指针
struct TreeNode **stack = (struct TreeNode **) malloc (sizeof(struct TreeNode *) * 101);
//用来存储二叉树的中序序列
int* a = (int *) malloc (sizeof(int) * 101);
//作为栈的指针
int top = 0;
//数组的下标
*returnSize = 0;
//关于这里为什么是||,因为最开始top=0.假设root不为NULL
//那么循环条件为真,继续执行,直到后面root可能为空的时候
//这时栈里还有元素top>0,就可以继续执行了
//可以自己带进去看一下,更好理解
while(root || top > 0)
{
//沿着二叉树最左的一条路径向下,并依次将指向结点的指针入栈
while(root)
{
stack[top++] = root;
root = root->left;
}
//由于上面循环结束的时候root为NULL,所以弹栈
root = stack[--top];
//此时root指向的结点就为最左的结点,将它并入数组中
a[(*returnSize)++] = root->val;
//再遍历它的右子树
root = root->right;
}
return a;
}
该算法的时间复杂度为 O ( n ) O(n) O(n),空间复杂度为 O ( n ) O(n) O(n)。
第二种算法就是 m o r r i s morris morris中序遍历。
它能将上面算法的空间复杂度降为 O ( 1 ) O(1) O(1)。 m i r r i s mirris mirris遍历主要就是取消了用栈的方式来间接实现递归,用一个指针操作即可,也可以说是它利用了中序遍历的前驱和后继之间的关系。比较难懂,先介绍它的步骤( c u r cur cur为当前遍历到的结点)和代码,例子在后面:
- 若 c u r cur cur无左孩子,则将它的 v a l val val添加到数组中(用数组来存储二叉树的中序遍历序列),再访问 c u r cur cur的右孩子
- 若 c u r cur cur有左孩子,则首先找到左子树中最右的结点(也可以理解为 c u r cur cur的前驱),并让 p r e pre pre指向它,随后判断 p r e pre pre的右孩子:
- 若它的右孩子为空,则将其右孩子指向 c u r cur cur,然后访问 c u r cur cur的左孩子。相当于执行 p r e − > n e x t = c u r pre->next = cur pre−>next=cur(前驱和后继连起来了)和 c u r = c u r − > l e f t cur = cur->left cur=cur−>left
- 若它的右孩子不为空(说明此时它的右孩子为它的后继),则此时我们已经遍历完了 c u r cur cur的左子树,将 p r e pre pre的右孩子指向NULL,然后将 c u r cur cur的 v a l val val添加到数组中,然后访问 c u r cur cur的右孩子。
struct TreeNode
{
int val;
struct TreeNode *left;
struct TreeNode *right;
};
int* inorderTraversal(struct TreeNode* cur, int* returnSize)
{
int* t = (int *) malloc (sizeof(int) * 100);
struct TreeNode *pre = NULL;
*returnSize = 0;
while(cur)
{
if(cur->left)
{
pre = cur->left;
while(pre->right && pre->right != cur)
{
pre = pre->right;
}
if(!pre->right)
{
pre->right = cur;
cur = cur->left;
}
else
{
t[(*returnSize)++] = cur->val;
pre->right = NULL;
cur = cur->right;
}
}
else
{
t[(*returnSize)++] = cur->val;
cur = cur->right;
}
}
return t;
}
看下图,对下图进行 m o r r i s morris morris遍历:
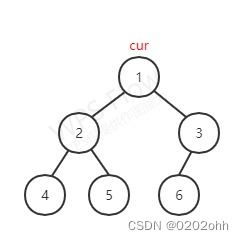
此时 c u r cur cur指向根结点,按照上述步骤,它有左孩子,那么使 p r e pre pre指向它左子树最右的结点,如下图: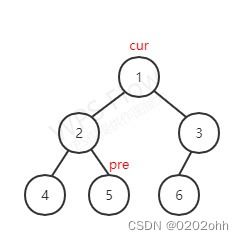
此时 p r e pre pre的右孩子为空,那么按照上述步骤,将 p r e pre pre的右孩子指向 c u r cur cur,并使 c u r cur cur指向它的左孩子,如下图: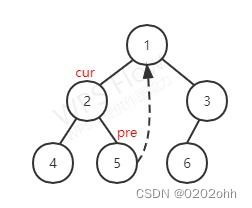
至此,一次循环结束。(最外层循环的条件为 c u r cur cur不为空)
又由上图知,并按照上述步骤, c u r cur cur有左孩子,那么就使 p r e pre pre指向它左子树最右的结点,如下图:
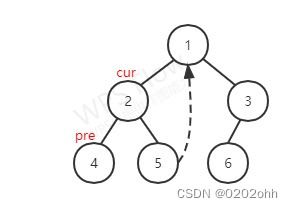
又按照上述步骤, p r e pre pre的右孩子为空,再将 p r e pre pre的右孩子指向 c u r cur cur,并且 c u r cur cur指向它的左孩子,如下图: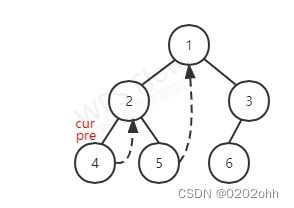
至此,第二次循环结束。
然后 c u r cur cur不为空,按照上述步骤, c u r cur cur无左孩子,将它的 v a l val val添加到数组中,再访问 c u r cur cur的右孩子(注意,它的右孩子不为空了,仔细看上图),如下图: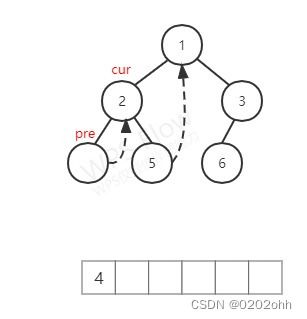
至此,第三次循环结束。
然后,又按照上述步骤,此时 c u r cur cur有左孩子,又找到 c u r cur cur左子树中最右结点,并使 p r e pre pre指向它(这里跟上图没什么变化),然后继续判断, p r e pre pre的右孩子不为空,说明 c u r cur cur的左子树已遍历完,将 c u r cur cur的 v a l val val添加到数组中,并使 p r e pre pre的右孩子指向NULL,然后访问 c u r cur cur的右孩子,如下图: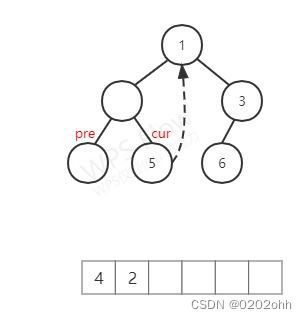
至此,第四次循环结束。
c u r cur cur不为空,又按照上述步骤, c u r cur cur无左子树,将 c u r cur cur的 v a l val val添加到数组中,再访问它的右孩子(注意它的右孩子为它的后继了),如下图:
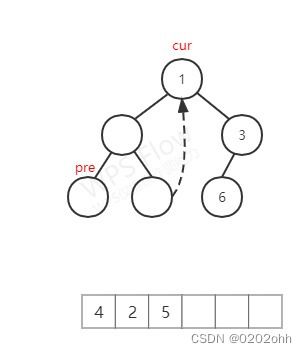
至此,第五次循环结束。
c u r cur cur不为空,它有左孩子,那么使 p r e pre pre指向它左子树中最右的结点,如下图: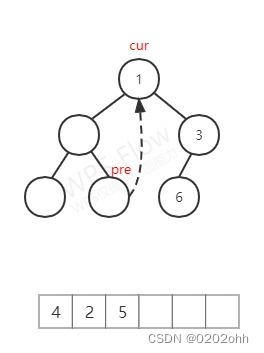
此时 p r e pre pre的右孩子不为空,那么此时已遍历完 c u r cur cur的左子树,将 c u r cur cur的 v a l val val添加到数组中,并使 p r e pre pre的右孩子指向NULL,然后再访问 c u r cur cur的右孩子,如下图: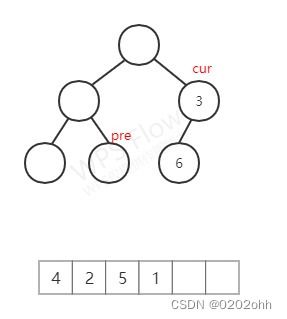
至此,第六次循环结束。
c u r cur cur不为空,且它有左子树,按照上述步骤,使 p r e pre pre指向它左子树中最后的结点,如下图: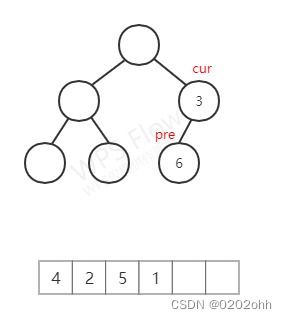
p r e pre pre的右孩子为空,按照上述步骤, p r e pre pre的右孩子指向 c u r cur cur, c u r cur cur再访问它的左孩子,如下图: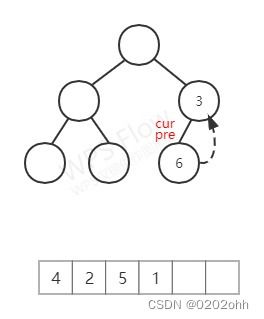
至此,第七次循环结束。
c u r cur cur不为空,但没有左子树,按照上述步骤,将它的 v a l val val添加到数组,再访问它的右孩子(注意,再之前pre已经将该结点的右孩子指向了3),如下图: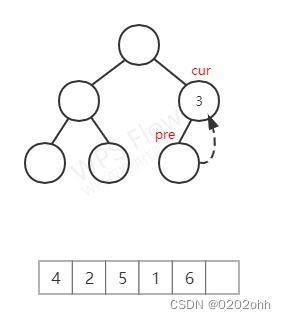
至此,第八次循环结束。
c u r cur cur不为空,有左孩子,按照上述步骤,将 p r e pre pre指向它左子树中最右的结点(这里跟上图一样的),然后, p r e pre pre的右孩子不为空,按照上述步骤,则此时已经遍历完了 c u r cur cur的左子树,那么将 c u r cur cur的 v a l val val添加到数组中,再将 p r e pre pre的右孩子指向NULL,然后访问 c u r cur cur的右孩子,如下图: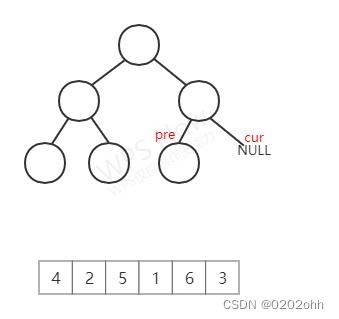
至此,第9次循环结束。
c u r cur cur为空,循环结束,返回数组的首地址。
morris遍历,主要就是利用前驱和后继的关系来实现二叉树的中序遍历,多举例子试一下,印象就深刻了。