【算法】滑动窗口题单——4.不定长滑动窗口(求子数组个数)
文章目录
- 前言
- 2799. 统计完全子数组的数目
-
- 解法1——枚举右端点,移动左端点
- 解法2——枚举左端点,扩展右端点
- 713. 乘积小于 K 的子数组
- 1358. 包含所有三种字符的子字符串数目
- 2302. 统计得分小于 K 的子数组数目
- 2537. 统计好子数组的数目
- 2762. 不间断子数组(滑动窗口+)
-
- 解法1——TreeMap
- 解法2——单调队列
题单来源:https://leetcode.cn/problems/minimum-size-subarray-in-infinite-array/solutions/2464878/hua-dong-chuang-kou-on-shi-jian-o1-kong-cqawc/
前言
这些问题常用的方法有:
- 枚举左端点,扩展右端点。
- 枚举右端点,收缩左端点。
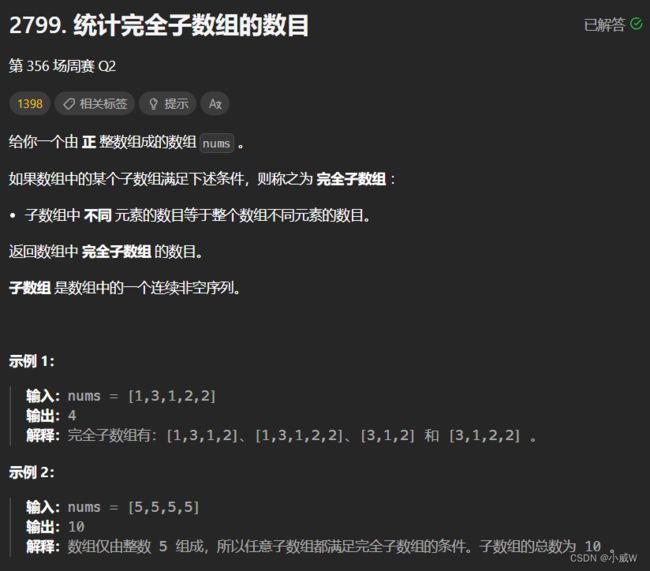
2799. 统计完全子数组的数目
https://leetcode.cn/problems/count-complete-subarrays-in-an-array/description/
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 2000
解法1——枚举右端点,移动左端点
class Solution {
public int countCompleteSubarrays(int[] nums) {
Set<Integer> s = new HashSet();
for (int num: nums) s.add(num);
int n = nums.length, sum = s.size(), ans = 0;
Map<Integer, Integer> m = new HashMap();
for (int r = 0, l = 0; r < n; ++r) {
m.merge(nums[r], 1, Integer::sum);
while (m.get(nums[l]) > 1) {
m.merge(nums[l], -1, Integer::sum);
l++;
}
if (m.size() == sum) ans += l + 1;
}
return ans;
}
}
解法2——枚举左端点,扩展右端点
class Solution {
public int countCompleteSubarrays(int[] nums) {
Set<Integer> set = new HashSet<>();
Map<Integer, Integer> map = new HashMap<>();
for (int num: nums) set.add(num);
int x = set.size(), n = nums.length, ans = 0;
for (int l = 0, r = 0; l < n; ++l) {
while (r < n && map.size() < x) map.merge(nums[r++], 1, Integer::sum);
if (map.size() == x) ans += n - r + 1;
map.merge(nums[l], -1, Integer::sum);
if (map.get(nums[l]) == 0) map.remove(nums[l]);
}
return ans;
}
}
713. 乘积小于 K 的子数组
https://leetcode.cn/problems/subarray-product-less-than-k/description/
提示:
1 <= nums.length <= 3 * 10^4
1 <= nums[i] <= 1000
0 <= k <= 10^6
枚举右端点,根据窗口内的乘积大小移动左端点。
当 [ l , r ] [l,r] [l,r]范围内的乘积符合条件时,一共有r-l+1个子数组符合条件计入答案,分别为 [ l + 1 , r ] , [ l + 2 , r ] , . . . , [ r , r ] [l+1,r],[l+2,r],...,[r,r] [l+1,r],[l+2,r],...,[r,r]。
class Solution {
public int numSubarrayProductLessThanK(int[] nums, int k) {
int n = nums.length, mul = 1, ans = 0;
for (int l = 0, r = 0; r < n; ++r) {
mul *= nums[r];
while (l <= r && mul >= k) mul /= nums[l++];
ans += r - l + 1;
}
return ans;
}
}
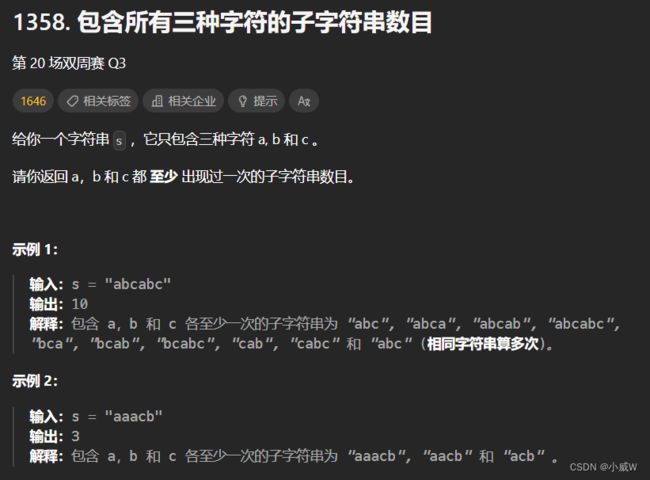
1358. 包含所有三种字符的子字符串数目
https://leetcode.cn/problems/number-of-substrings-containing-all-three-characters/description/
提示:
3 <= s.length <= 5 x 10^4
s 只包含字符 a,b 和 c ·
使用 c n t [ ] cnt[] cnt[] 数组维护窗口中各个字母的数量。
枚举左端点,拓展右端点,当 [ l , r ] [l,r] [l,r]符合条件时,所有的 [ l , r ] , [ l , r + 1 ] , . . . [ l , n − 1 ] [l,r],[l,r+1],...[l,n-1] [l,r],[l,r+1],...[l,n−1]都符合条件,计入答案。
class Solution {
public int numberOfSubstrings(String s) {
int[] cnt = new int[3];
int ans = 0, n = s.length();
for (int l = 0, r = 0; l < n; ++l) {
while (r < n && !check(cnt)) cnt[s.charAt(r++) - 'a']++;
if (check(cnt)) ans += n - r + 1;
else break; // 已经不可能有答案了
cnt[s.charAt(l) - 'a']--;
}
return ans;
}
public boolean check(int[] cnt) {
return cnt[0] != 0 && cnt[1] != 0 && cnt[2] != 0;
}
}
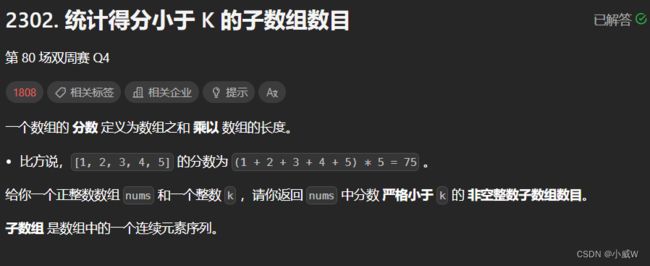
2302. 统计得分小于 K 的子数组数目
https://leetcode.cn/problems/count-subarrays-with-score-less-than-k/description/
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5
1 <= k <= 10^15
枚举右端点,根据窗口情况移动左端点。
当窗口 [ l , r ] [l,r] [l,r]满足条件时,所有 [ l + 1 , r ] , [ l + 2 , r ] , . . . , [ r , r ] [l+1,r],[l+2,r],...,[r,r] [l+1,r],[l+2,r],...,[r,r]都满足条件。
class Solution {
public long countSubarrays(int[] nums, long k) {
long ans = 0, s = 0;
for (int l = 0, r = 0; r < nums.length; ++r) {
s += nums[r];
while (s * (r - l + 1) >= k) s -= nums[l++];
ans += r - l + 1;
}
return ans;
}
}
2537. 统计好子数组的数目
https://leetcode.cn/problems/count-the-number-of-good-subarrays/description/
提示:
1 <= nums.length <= 10^5
1 <= nums[i], k <= 10^9
哈希表记录各个元素出现的数量,cnt记录符合条件的下标对数。
枚举窗口的左端点,为了让窗口符合条件扩展右端点。(符合条件之后,所有比当前右端点更靠右的下标作为右端点一定也符合条件。)
class Solution {
public long countGood(int[] nums, int k) {
long ans = 0;
Map<Integer, Integer> m = new HashMap<>();
int n = nums.length, cnt = 0; // cnt记录下标对数
// 枚举左端点,扩展右端点
for (int l = 0, r = 0; l < n; ++l) {
while (r < n && cnt < k) {
m.merge(nums[r], 1, Integer::sum);
cnt += m.get(nums[r]) - 1;
r++;
}
if (cnt >= k) ans += n - r + 1;
else break;
m.merge(nums[l], -1, Integer::sum);
cnt -= m.get(nums[l]);
}
return ans;
}
}
2762. 不间断子数组(滑动窗口+)
https://leetcode.cn/problems/continuous-subarrays/description/
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
使用滑动窗口,维护窗口内的最大值和最小值有多种方法。
解法1——TreeMap
TreeMap 会对 key 自动排序,并且有方便的 api 获取最大key和最小key。
class Solution {
public long continuousSubarrays(int[] nums) {
long ans = 0;
int n = nums.length;
TreeMap<Integer, Integer> s = new TreeMap<>();
for (int l = 0, r = 0; r < n; ++r) {
s.merge(nums[r], 1, Integer::sum);
while (s.lastKey() - s.firstKey() > 2) {
s.merge(nums[l], -1, Integer::sum);
if (s.get(nums[l]) == 0) s.remove(nums[l]);
l++;
}
ans += r - l + 1;
}
return ans;
}
}
解法2——单调队列
两个单调队列分别维护窗口中的最大值和最小值
class Solution {
public long continuousSubarrays(int[] nums) {
long ans = 0;
// dq1从大到小,dq2从小到大
Deque<Integer> dq1 = new ArrayDeque(), dq2 = new ArrayDeque();
for (int i = 0, j = 0; i < nums.length; ++i) {
// 处理两个单调队列
while (!dq1.isEmpty() && nums[i] > nums[dq1.peekLast()]) dq1.pollLast();
while (!dq2.isEmpty() && nums[i] < nums[dq2.peekLast()]) dq2.pollLast();
dq1.offerLast(i);
dq2.offerLast(i);
while (nums[dq1.peekFirst()] > nums[dq2.peekFirst()] + 2) {
if (dq1.peekFirst() < dq2.peekFirst()) {
j = dq1.peekFirst() + 1;
dq1.pollFirst();
}
else {
j = dq2.peekFirst() + 1;
dq2.pollFirst();
}
}
ans += i - j + 1;
}
return ans;
}
}