剑指数组c++

  

两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。

  经典的哈希表问题。我们用哈希表记录每个值的下标，当合适的数值出现时我们就能直接获得该数值的下标。

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        vector<int> res;
        unordered_map<int,int> hashmap;
        for(int i=0;i<nums.size();i++){
            if(hashmap.count(target-nums[i])!=0){
                res.push_back(i);
                res.push_back(hashmap[target-nums[i]]);
                break;
            }
            hashmap[nums[i]] = i;
        }
        return res;
    }
};

剑指 Offer 03. 数组中重复的数字

  同哈希表问题，贴一个答案就好了。

class Solution {
public:
    int findRepeatNumber(vector<int>& nums) {
        unordered_set<int> hashset;
        for(int i=0;i<nums.size();i++){
            if(hashset.count(nums[i])==0){
                hashset.insert(nums[i]);
            }else{
                return nums[i];
            }
        }
        return 0;
    }
};

三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。
注意：答案中不可以包含重复的三元组。
  三数之和是很经典的题了，该题目考察了双指针以及双指针中的去重操作。
  首先，如果我们对数组进行了排序，那么我们肯定abc是顺序出现的，a最小,b其次，c最大。
  每次循环，我们先定位出a，由于我们三个数之和是0，最小的数肯定是负数，再加上不允许重复，我们就必须要保证a是负数并且是相同的数里面的最后一个。
  定位好a之后我们去a的后面找b和c。
  bc使用双指针进行定位，b起始是a的后一位，c起始是数组最后一位。
  根据abc的和不断修正bc的位置，这里要注意，如果找到了一个答案之后，我们要检测b的右边是不是和b一样，c的左边是不是和c一样，为了避免重复，我们应当跳过这些元素。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> result;
        if(nums.empty()||nums.size()<3) return result; 
        sort(nums.begin(), nums.end());//abc肯定是顺序的，不多说直接排序遍历
        for(int i=0;i<nums.size();i++){
            if(nums[i]>0){//如果当前起点成正数就不想了，因为a肯定是负数！
                return result;
            }
            if(i>0&&nums[i-1]==nums[i]){//如果有相同的起点就跳到最后一个相同的数当起点！
                continue;
            }
            //好了，i就是a了，我们去找b和c
            int left = i+1;//双指针！
            int right = nums.size()-1;
            while(left<right){
                if(nums[i]+nums[left]+nums[right] == 0){//关键，找到b和c了再怎么办
                    result.push_back({nums[i],nums[left],nums[right]});//先把答案记录了
                    while(left<right&&nums[left]==nums[left+1]){//{1,1,0,2,2}出现这种情况怎么办？为了防止有重复答案我们要跳过第二个1和倒数第二个2！
                        left++;
                    }
                    while(left<right&&nums[right]==nums[right-1]){
                        right--;
                    }
                    left++;//注意还要再移动一位才能完全摆脱和之前相同的值
                    right--;
                }else if(nums[i]+nums[left]+nums[right] >0){//如果超了，右边往里缩
                    right--;
                }else{//如果少了，左边往里走
                    left++;
                }
            }
        }
        return result;
    }
};

寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
  我们还是用简单一些的方法处理这个问题，我们新建一个数组，把nums1和nums2按顺序放进去，然后直接按下标找中位数。

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len1 = nums1.size();
        int len2 = nums2.size();
        int length = len1 + len2;
        vector<int> target(length,0);//用一个数组存下nums1 和 nums2
        int i=0,j=0;
        int index = 0;
        while(i<len1&&j<len2){//如果有一个到头了就不能这样算了
            if(nums1[i]<nums2[j]){
                target[index++] = nums1[i++];
            }else{
                target[index++] = nums2[j++];
            }
        }
        if(i==len1){//如果nums1到头
            for(int k=j;k<len2;k++){//把nums2的都加上
                target[index++] = nums2[k];
            }
        }else if(j==len2){//如果nums2到头
            for(int k=i;k<len1;k++){//把nums1的都加上
                target[index++] = nums1[k];
            }
        }
        if(length%2 == 0){
            int mid = (length-1)/2;
            return (double)(target[mid] + target[mid+1])/2;
        }else{
            int mid = (length)/2;
            return (double)target[mid];
        }
    }
};

接雨水

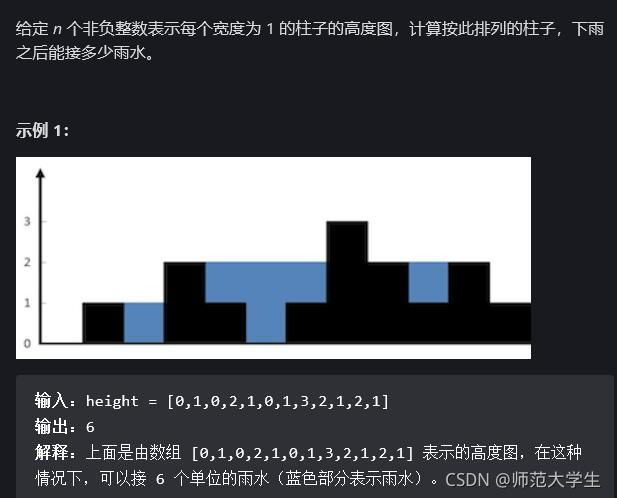  接雨水的核心在于，怎么去计算雨水的体积。
  一个纵向单位的雨水体积 = 右侧最高高度和左侧最高高度的最小值 - 自己的滴珠高度。
  所以我们创建两个数组，分别记录所有单位左侧最高高度和右侧最高高度就好了。

class Solution {
public:
    int trap(vector<int>& height) {
        int sum = 0;
        vector<int> maxleft(height.size(),0);//记录对于每个点来说，最大的左侧高度
        vector<int> maxright(height.size(),0);//记录对于每个点来说，最大的右侧高度
        maxleft[0] = height[0];
        for(int i=1;i<height.size();i++){//左边最大值是从左往右递推
            maxleft[i] = max(height[i],maxleft[i-1]);//递推求最大，拿自己和前一个位置的最大值比！
        }
        maxright[height.size()-1] = height[height.size()-1];
        for(int i = height.size()-2;i>=0;i--){//右边最大值是从右往左递推
            maxright[i] = max(height[i],maxright[i+1]);//拿自己和后一个位置的最大值比！
        }
        
        for(int i=0;i<height.size();i++){
            int count = min(maxleft[i],maxright[i]) - height[i];//计算每个纵向单位的雨水体积
            if(count>0) sum += count;
        }
        return sum;
    }
};

合并两个有序数组

  这个题是上个题的子集。

class Solution {
public:
    void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int i=0,j=0;
        vector<int> sorted(m+n,0);
        int index = 0;
        while(i<m&&j<n){
            if(nums1[i]>nums2[j]){
                sorted[index++] = nums2[j++];
            }else{
                sorted[index++] = nums1[i++];
            }
        }
        if(i==m){
            for(int k=j;k<n;k++){
                sorted[index++] = nums2[k];
            }
        }else if(j==n){
            for(int k=i;k<m;k++){
                sorted[index++] = nums1[k];
            }
        }
        for(int i=0;i<m+n;i++){
            nums1[i] = sorted[i];
        }
    }
};

全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
  同枝剪枝的回溯问题，回溯模板题。

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums,vector<bool>& used){
        if(path.size()==nums.size()){
            result.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(used[i]==true) continue;//在当前的分支里就不能用这个数字了
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums,used);
            path.pop_back();//回溯操作
            used[i] = false;
        }
    }

    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size(),false);
        backtracking(nums,used);
        return result;
    }
};

剑指 Offer 42. 连续子数组的最大和

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
要求时间复杂度为O(n)。
  我们这里用动态规划处理一下这个题。
  dp[i]表示到达下标i时连续子数组的最大和。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.empty()){
            return 0;
        }
        vector<int> dp(nums.size(),0);
        dp[0] = nums[0];//第一个元素不用比
        int ans = nums[0];//保底是第一个元素，当然设成int最小值也没问题
        for(int i=1;i<nums.size();i++){
            dp[i] = max(nums[i],dp[i-1]+nums[i]);//要么是之前的累加+当前元素，要么只选当前元素放弃之前累加
            ans = max(dp[i],ans);//随时记录最大值
        }
        return ans;
    }
};

岛屿数量

  岛屿数量太经典dfs了，直接说代码吧。
  可以注意一下在dfs代码中，我们没有显式使用return来结束搜索，为什么呢？
  因为我们在遍历一个陆地后会将其改成海，搜索着总有一天就没陆地了，到时候dfs里的四个方向判断都不成立，自然就停止搜索了。

class Solution{
public:
    void dfs(vector<vector<char>>& grid,int i,int j){
        int rows = grid.size();
        int colomns = grid[0].size();
        grid[i][j] = '0';//改成海洋，不会重复搜索
        if(i+1<rows&&grid[i+1][j] == '1') dfs(grid,i+1,j);//因为有方向的判断，所以会自动结束搜索
        if(i-1>=0&&grid[i-1][j] == '1') dfs(grid,i-1,j);
        if(j+1<colomns&&grid[i][j+1] == '1') dfs(grid,i,j+1);
        if(j-1>=0&&grid[i][j-1] == '1') dfs(grid,i,j-1);
    }

    int numIslands(vector<vector<char>>& grid){
        if(grid.empty()){
            return 0;
        }
        int rows = grid.size();
        int colomns = grid[0].size();
        int landsnum = 0;
        for(int i=0;i<rows;++i){
            for(int j=0;j<colomns;++j){
                if(grid[i][j] =='1'){
                    landsnum++;
                    dfs(grid,i,j);
                }
            }
        }
        return landsnum;
    }
};

缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

  我们只能遍历一次数组，并且不能额外开辟和数组一样长的空间。
  所以不能用暴力方法，建哈希表法和枚举遍历（也太暴力了）都不行。
  这里使用了一手置换法。
  我们可以想到，如果调整原数组的排列，使其尽力恢复成正数排序，但是会有一些位置上的数是错误的，每一个错误的位置就代表一个缺失的正数。
  这样，我们遍历数组，将遇到的在【1，n】范围内的数，都通过交换的方式移动到它应该在的位置上！然后再遍历寻找第一个不合适的就可以了。

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        int n = nums.size();
        for(int i=0;i<n;++i){
            while(nums[i]>=1&&nums[i]<=n&&nums[nums[i]-1]!=nums[i]){//最后一个条件是防止死循环
                swap(nums[i],nums[nums[i]-1]);//将该元素交换到该元素-1的下标处
            }
        }
        for(int i=0;i<n;++i){
            if(nums[i] != i+1){
                return i+1;
            }
        }
        return n+1;
    }
};

盛最多水的容器

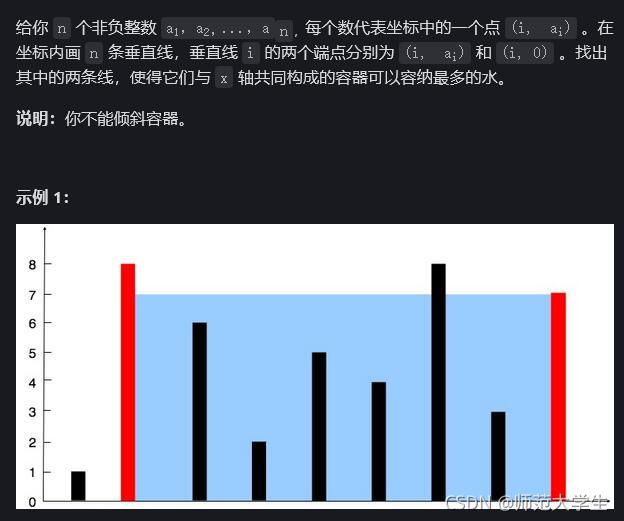  容器是一个经典的双指针问题，通过双指针我们可以方便地求出每块容器能盛水的体积。
  这道题的核心思想主要是双指针的移动方案：当左边比右边低时，左边往左移；右边比左边低时，右边往左移。
  这里其实体现了一种贪心的思想，水的体积是木桶效应，靠两边最短的边决定，我们每次都去改变相对较短的边，等于是不断谋求更长的边。

class Solution {
public:
    int maxArea(vector<int>& height) {
        if(height.empty()){
            return 0;
        }
        int left = 0;//双指针
        int right = height.size()-1;
        int ans = 0;
        while(left<right){
            ans = max(ans,(right-left)*min(height[left],height[right]));///计算公式，木桶效应
            if(height[left]<=height[right]){//贪心策略，哪边相对较短就移动哪边
                left++;
            }else{
                right--;
            }
        }
        return ans;
    }
};

排序数组

  排序方法很多了，我们这里记录一下归并排序。
  归并排序的核心思想：
  1.将原数组对半分，两边进行递归，分别得到两个有序数组。
  2.对有序数组进行合并。

class Solution {
public:
    vector<int> temp;
    void mergeSort(vector<int>&nums,int left,int right){
        if(left>=right) return;
        int mid = left + (right - left)/2;//找到当前数组长度的中点
        mergeSort(nums,left,mid);//中点前后分两段递归
        mergeSort(nums,mid+1,right);
        int i=left,j=mid+1;//i j分别是前后两端的起点
        int cnt = 0;
        while(i<=mid&&j<=right){//合并两个有序数组（前段和后段）
            if(nums[i]<=nums[j]){
                temp[cnt++] = nums[i++];
            }else{
                temp[cnt++] = nums[j++];
            }
        }
        while(i<=mid){//将剩余的也加入到temp中来
            temp[cnt++] = nums[i++];
        }
        while(j<=right){
            temp[cnt++] = nums[j++];
        }//temp现在就是合并好的数组
        for(int i=0;i<right-left+1;++i){//将temp中的内容转移到源数组区间里
            nums[left + i] = temp[i];//注意nums的区间要从left开始算起
        }
    }
    vector<int> sortArray(vector<int>& nums) {
        temp.resize(nums.size(),0);
        mergeSort(nums,0,nums.size()-1);
        return nums;
    }
};

合并区间

  合并区间的本质是一个贪心问题。
  我们首先使用每个元素的左边界进行排序。
  随后遍历数组，如果当前元素的起始值在前一个元素的结尾值前面，那么我们就直接更新end，直到条件不满足，再记录答案。
  注意我们需要额外处理最后一个元素，如果最后一个元素没有合并到区间里我们需要额外在答案里加上。

class Solution {
public:
    static bool compare(vector<int>& a,vector<int>& b){
        return a[0] < b[0];//用左边界进行比较 
    }

    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        sort(intervals.begin(),intervals.end(),compare);
        bool lastflag = false;//专门用来判断最后一个元素怎么处理
        //因为start 和 end 是前一个元素的，所以在最后一位需要特殊处理
        for(int i=1;i<intervals.size();++i){
            int start = intervals[i-1][0];//记录下前一个元素的起始
            int end = intervals[i-1][1];//前一个元素的结束
            while(i<intervals.size()&&intervals[i][0]<=end){//如果当前的起点在前一个元素区间内
                end = max(end,intervals[i][1]);//那么就更新结尾，当前的结尾和之前的结尾取最大值
                if(i==intervals.size()-1){//如果最后一位被合并了，那就不用管了
                    lastflag = true;
                }
                i++;//直接找下一个元素
            }
            res.push_back({start,end});//说明不重合了，记录答案
        }
        if(lastflag == false){//最后一位如果没合并，可得最后加上
            res.push_back({intervals[intervals.size()-1][0],intervals[intervals.size()-1][1]});
        }
        return res;
    }
};

分发糖果

  当我们遇到一个数组，要求每个元素和左右两个都有关系时，最好把问题拆解，从左边遍历计算一次，从右边遍历再计算一次。

class Solution {
public:
    int candy(vector<int>& ratings) {
        if(ratings.empty()) return 0;
        vector<int> candy(ratings.size(),1);
        int ans=0;
        for(int i=1;i<ratings.size();i++){//先从左边开始遍历，给更大的更多糖
            if(ratings[i]>ratings[i-1]){
                candy[i] = candy[i-1] + 1;
            }
        }
        for(int i=ratings.size()-2;i>=0;i--){//再从右边开始遍历，但是不能直接累加，需要和原先的进行对比
            if(ratings[i]>ratings[i+1]){
                candy[i] = max(candy[i],candy[i+1] + 1);
            }
        }
        for(auto temp:candy){
            ans += temp;
        }
        return ans;
    }
};

每日温度

  这个问题是非常典型的单调栈问题。
  我们构建一个单调栈，里面存元素的下标。栈里下标对应的温度从栈顶到栈底是递增的。这样，有更高的温度进来时，就可以把比它温度低的都弹出去，并记录答案。

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        vector<int> res(temperatures.size(),0);
        stack<int> st;//单调栈 从栈顶到栈底依次增大
        st.push(0);
        for(int i=1;i<temperatures.size();i++){//在单调栈里就三种情况
            if(temperatures[i]<temperatures[st.top()]){//新温度比栈顶低
                st.push(i);//加到栈里
            }else if(temperatures[i] == temperatures[st.top()]){//新温度和栈顶一样
                st.push(i);//加到栈里
            }else{//新温度比栈顶高，要做单调栈修改操作 
                while(!st.empty()&&temperatures[st.top()] < temperatures[i]){//将栈里比新温度低的都弹出来，同时记录答案
                    res[st.top()] = i - st.top();//记录答案
                    st.pop();//弹出栈
                }
                st.push(i);//最后将元素加入栈
            }
        }
        return res;
    }
};

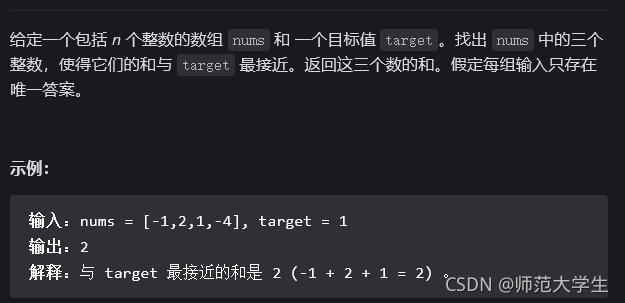
最接近的三数之和

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        int ans = nums[0] + nums[1] + nums[2];
        for(int i=0;i<nums.size();i++){
            int start = i+1,end = nums.size()-1;
            while(start<end){
                int sum = nums[i] + nums[start] + nums[end];//先计算一开始的和
                if(abs(target-sum)<abs(target-ans)){//更新答案
                    ans = sum;
                }
                if(sum>target){//如果比目标大，右边界移动
                    end--;
                }else if(sum<target){//比目标小，左边界移动
                    start++;
                }else{
                    return ans;
                }
            }
        }
        return ans;
    }
};

剑指 Offer 40. 最小的k个数

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。
  这里我们通过大根堆解决这个额问题，求最小用大根堆，求最大用小根堆。

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> res(k,0);
        if(k==0){
            return res;
        }
        priority_queue<int> myqueue;//创建优先队列,大顶堆！
        for(int i=0;i<k;++i){//先将数组前k个元素都塞进优先队列
            myqueue.push(arr[i]);
        }
        
        for(int i=k;i<arr.size();i++){//随后遍历数组剩余的元素
            if(myqueue.top() > arr[i]){//如果新的元素小于优先队列最前端元素，大顶，顶端是队列里最大的
                myqueue.pop();//就将最前端元素换成新元素，注意优先队列里面第一个元素是最大的，这样就逐渐将最大的元素换掉
                myqueue.push(arr[i]);//这样队列里的数整体就会越变越小，因为其中最大的一直被更小的数替换！
            }
        }

        for(int i=0;i<k;i++){//最后将优先队列的前k个赋值给答案数组！
            res[i] = myqueue.top();
            myqueue.pop();
        }
        return res;
    }
};

前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

  同样，我们用小顶堆实现这个问题。

class Solution {
public:
    class mycomparison{
        public:
        bool operator()(const pair<int,int>& lhs,const pair<int,int>& rhs){
            return lhs.second > rhs.second;
        }
    };
    vector<int> topKFrequent(vector<int>& nums, int k) {
        unordered_map<int,int> hashmap;//先做一个哈希表
        for(int i=0;i<nums.size();++i){//去记录每个元素的次数
            hashmap[nums[i]]++;
        }

        priority_queue<pair<int,int>,vector<pair<int,int>>,mycomparison> pri_que;//小根堆

        for(auto it = hashmap.begin();it!=hashmap.end();++it){//遍历哈希表
            pri_que.push(*it);//往小根堆里放元素
            if(pri_que.size()>k){//超过k了就把其中最小的弹出去
                pri_que.pop();
            }
        }
        
        vector<int> result(k);
        for(int i=k-1;i>=0;i--){//把小根堆里面的取出来，注意要倒着取
            result[i] = pri_que.top().first;
            pri_que.pop();
        }
        return result;
    }
};

  代码中我们可以看到，用小根堆求最大k，和用大根堆求最小k代码近似：
  大根堆求最小k，我们先将k个元素放进去，当后来的元素大于大根堆的顶端元素值时，弹出顶端元素，并压入新元素。
  小根堆求最大k，我们也可以先将k个元素放进去，当后来的元素大于大根堆的顶端元素值时，弹出顶端元素，并压入新元素。
  根本原因在于，大根堆的顶端是最大的元素，我们不断地将最大的元素用更小的元素去替换，这样队列整体会越来越小，我们就能得到最小的k个值。而小根堆的顶端是最小值，我们不断地用更大的元素去替换最小值，这样队列整体会越来越大，我们就能得到最大的k个值。
  当然我们也可以直接往队列里面加，如果队列长度大于k了，就弹出顶端的元素。
  以下两种写法都是正确的！

				/*for(int i=0;i arr[i]){//如果新的元素小于优先队列最前端元素，大顶，顶端是队列里最大的
                myqueue.pop();//就将最前端元素换成新元素，注意优先队列里面第一个元素是最大的，这样就逐渐将最大的元素换掉
                myqueue.push(arr[i]);
            }
        }*/
        for(int i = 0;i<arr.size();i++){
            myqueue.push(arr[i]);
            if(myqueue.size()>k){
                myqueue.pop();
            }
        }

从前序与中序遍历序列构造二叉树

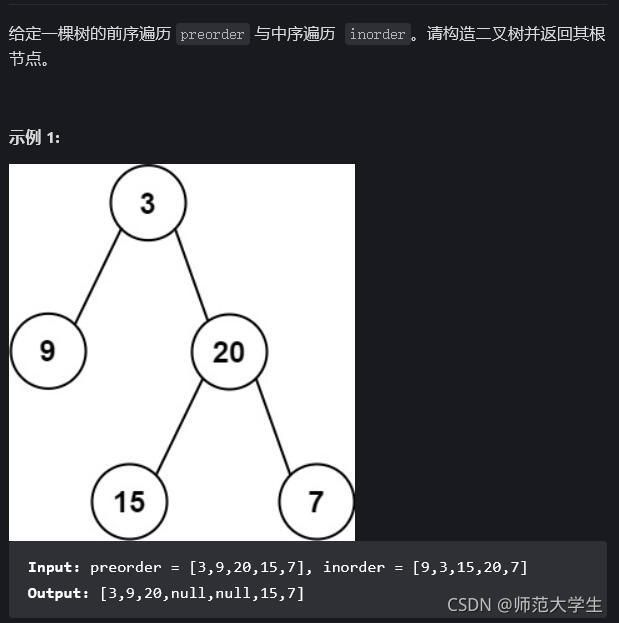  重构二叉树本身也是用到了递归的思想。
  前序遍历是根左右，中序遍历是左根右，我们可以从前序遍历中找到根节点，随后用该根节点在中序遍历中划分左右子树，再递归。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;
        
        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd; 

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;

        // 参数坚持左闭右开的原则
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

class Solution {
public:
    vector<int> preorder;
    unordered_map<int,int> dic;

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        this->preorder = preorder;
        for(int i=0;i<inorder.size();i++){
            dic[inorder[i]] = i; //哈希表，键是元素的值，键值是元素的坐标，用于划分中序排列数组
        }
        return recur(0,0,inorder.size()-1);
    }

    TreeNode* recur(int root,int left,int right){
        if(left>right) return nullptr; //终止递归操作
        TreeNode* node = new TreeNode(preorder[root]); //建立一个根节点,root就是前序排列数组中根节点的坐标
        int i = dic[preorder[root]]; //划分根节点 左子树 右子树，i是按照中序排列数组划分的
        node->left = recur(root+1,left,i-1);//左子树 主要是root取值的变化
        node->right = recur(root+i-left+1,i+1,right);//右子树
        return node;//回溯 将根节点返回
    }
};

剑指 Offer 29. 顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字
  模拟一个四方向顺时针的数组遍历。

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> ans;
        if(matrix.empty()){
            return ans;
        }
        if(matrix[0].empty()){
            return ans;
        }
        int rows = matrix.size();
        int colomns = matrix[0].size();
        int up = 0,down = rows-1,left = 0,right = colomns-1;
        while(up<=down&&left<=right){
            int i = up,j = left;
            //向右运动！
            while(j<=right){
                ans.push_back(matrix[i][j]);
                j++;
            }
            j--;//因为最后一次多加了一个1
            i++;up++;//因为第一层遍历完了，再也用不上了，所以标记的最高层要+1
            if(up>down) break;
            //向下运动！
            while(i<=down){
                ans.push_back(matrix[i][j]);
                i++;
            }
            i--;
            j--;right--;
            if(left>right) break;
            //向左运动
            while(j>=left){
                ans.push_back(matrix[i][j]);
                j--;
            }
            j++;
            i--;down--;
            if(up>down) break;
            //向上运动
            while(i>=up){
                ans.push_back(matrix[i][j]);
                i--;
            }
            left++;
            if(left>right) break;
        }
        return ans;
    }
};

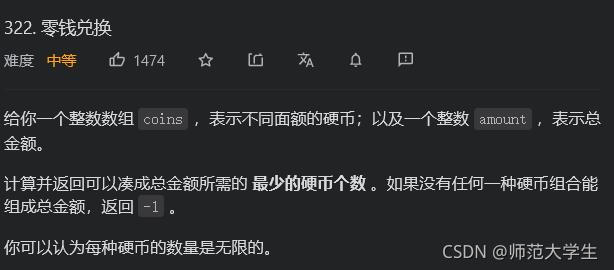
零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。
你可以认为每种硬币的数量是无限的。
  显然是一个完全背包问题，我们可以拿任意数量的硬币去组合amount。
  我们需要缕清，背包问题是求固定容量下的最大价值，或者求固定容量下的组合方式数量。
  这个问题中，我们求的是固定金额下的组合方式数量，amount即是目标价值又是最大容量，我们用amount当最大容量，同时用dp[amount]代表组合方式数量。

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {//完全背包问题
        vector<int> dp(amount+1,INT_MAX);//因为是比小，所以初始化最大
        dp[0] = 0;//0容量需要0个硬币
        for(int i=0;i<coins.size();i++){//遍历硬币
            for(int j=coins[i];j<=amount;j++){//遍历容量，找到装满背包的方法数量
                if(dp[j-coins[i]]!=INT_MAX)//如果存在
                dp[j] = min(dp[j],dp[j-coins[i]]+1);//总额为j-coins[i]的最少个数为dp[j-coins[i]]，再加上coins[i]的话，金币个数再加1
            }
        }
        if(dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

删除有序数组中的重复项

给你一个有序数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。
不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
  原地修改数组往往需要双指针技术。我们需要返回的是长度，我们可以想象通过双指针中的快慢指针来实现不重复数组的长度统计。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int fast = 1, slow = 1;
        while (fast < n) {
            if (nums[fast] != nums[fast - 1]) {
                nums[slow] = nums[fast];//慢指针在快指针判断不相同时，才将快指针记录，并前进
                ++slow;
            }
            ++fast;//快指针不断移动,无论是重复了还是不重复 
        }
        return slow;
    }
};

和为 K 的子数组

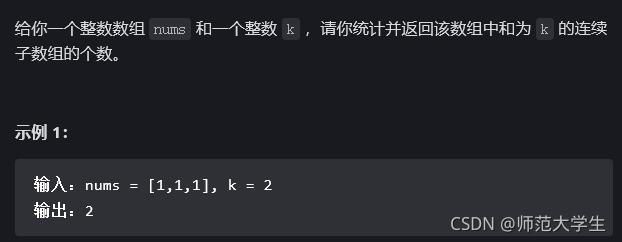
  看到这个题其实可以想到暴力法，直接从任意一个点出发，去依次遍历剩下的元素做累加和，并判断是否可以累加成目标值。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        for(int left = 0;left<nums.size();left++){
            int sum = 0;
            for(int right = left;right<nums.size();right++){
                sum += nums[right];
                if(sum == k) count++;
            }
        }
        return count;
    }
};

  但是这样太捞了，过不了。
  我们想到可以使用前缀和的思想来解决这个问题。
  前缀和数组里i下标的值，就代表原数组i下标之前的元素的总和。注意前缀和数组比源数组长一个单位，因为前缀和数组会把所有值的累加和当做最后一个元素。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        vector<int> pres(nums.size()+1,0);
        pres[0] = 0;
        for(int i=0;i<nums.size();i++){
            pres[i+1] = pres[i] + nums[i];//构建前缀和数组
        }
        for(int left = 0;left<nums.size();left++){
            for(int right = left;right<nums.size();right++){
                if(pres[right+1]-pres[left] == k){//注意right+1，因为前缀和数组比原数组长一个单位
                    count++;
                }
            }
        }
        return count;
    }
};

  前缀和+哈希表，进一步减少复杂度。
  我们将前缀和数组取消掉，将前缀和的出现次数存放到哈希表里，参照“两数之和”的思路解决此问题。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        unordered_map<int,int> mymap;//建立哈希表，存的是每个数值和对应的连续子数组个数
        mymap[0] = 1;
        int presum = 0;
        for(int x:nums){//遍历数组
            presum += x;//做包含当前元素的累加和
            if(mymap.count(presum-k)){//如果数值和-目标的值在数值和哈希表中存在
                count += mymap[presum-k];//就都加上
            }
            mymap[presum]++;//并将数值和的个数增加
        }
        return count;
    }
};

零钱兑换

  经典的完全背包问题。
  背包的容量就是价值，我们的计算公式是计算组合方式的，所以是

dp[j] = min(dp[j],dp[j-coins[i]]+1)

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {//完全背包问题
        vector<int> dp(amount+1,INT_MAX);//因为是比小，所以初始化最大
        dp[0] = 0;//0容量需要0个硬币
        for(int i=0;i<coins.size();i++){//遍历硬币
            for(int j=coins[i];j<=amount;j++){//遍历容量，找到装满背包的方法数量
                if(dp[j-coins[i]]!=INT_MAX)//如果存在
                dp[j] = min(dp[j],dp[j-coins[i]]+1);//总额为j-coins[i]的最少个数为dp[j-coins[i]]，再加上coins[i]的话，金币个数再加1
            }
        }
        if(dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

删除有序数组中的重复项

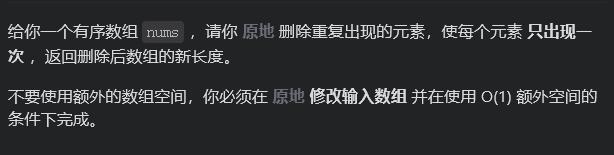
  题目要求返回长度，不过这个不重要，重要的是如何用原地修改输入数组的方式解决这个问题。
  一般原地修改数组，我们通常采用双指针的方法。再看这道题，我们要原地删除重复元素，数组是不可能原地删除的（又不是动态数组），实际上题目可以理解为，把重复的元素覆盖，再输出长度。综上，我们很容易联想到快慢指针。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int fast = 1, slow = 1;//初始位置是1，因为位置0（就一个元素）不会重复的
        while (fast < n) {
            if (nums[fast] != nums[fast - 1]) {//如果和之前的元素不重复。
                nums[slow] = nums[fast];//才将快指针记录到慢指针，并前进慢指针
                ++slow;
            }
            ++fast;//快指针不断移动，无论是否出现重复
        }
        return slow;
    }
};

打家劫舍

  这个问题是道十分经典的动态规划题目。
  根据此次房间的偷或者不偷进行递推。

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.empty()) return 0;
        if(nums.size()==1) return nums[0];
        if(nums.size()==2) return max(nums[0],nums[1]);//如果少于三家，就不需要递推了
        vector<int> dp(nums.size(),0);
        dp[0] = nums[0];
        dp[1] = max(nums[0],nums[1]);
        for(int i=2;i<nums.size();i++){
            dp[i] = max(dp[i-2]+nums[i],dp[i-1]);//到了当前的屋子，就两种选择：拿或者不拿
            //拿了，就必须从i-2处递推，没拿就直接从i-1递推
        }
        return dp[nums.size()-1];//肯定是偷到最后一家拿的钱最多
    }
};

剑指 Offer 11. 旋转数组的最小数字

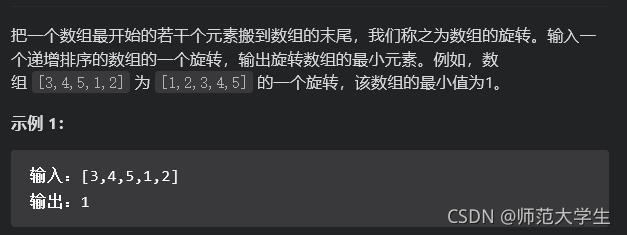  这道题似乎需要对二分查找做分情况处理，但是实际上也可以不这样做。
  通过中间元素和right处元素的对比可以直接二分，不过由于加了去重操作，复杂度有所退化。

class Solution {
public:
    int minArray(vector<int>& numbers) {
        if(numbers.empty()){
            return 0;
        }
        int left = 0;
        int right = numbers.size()-1;
        while(left<right){
            int mid = left + (right-left)/2;
            if(numbers[mid]<numbers[right]){//中间比右边小，转换点在左边，但是不确定是不是自己
                right = mid;
            }else if(numbers[mid]>numbers[right]){//中间比右边大，说明转换点一定在右边，肯定不是自己
                left = mid +1;
            }else{//去重操作，主动移动right
                right--;
            }
        }
        return numbers[right];
    }
};

最长连续序列

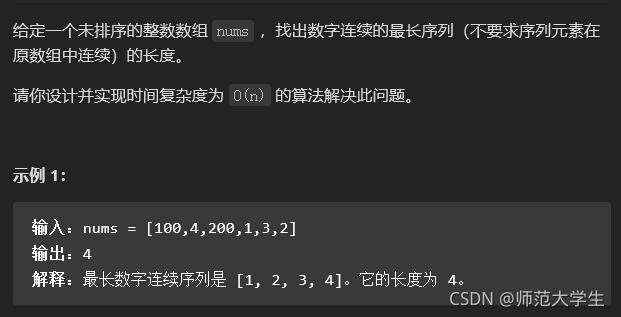  这个题对时间复杂度提了要求，所以不要去想排序之类的做法了。
  这道题使用了哈希集。我们将所有的元素先塞到哈希集里面。然后遍历哈希集的数字，如果某个数字的下一位也在哈希集里，那我们就去继续顺着更新答案。
  为了节省时间复杂度，我们提前做了去重，如果当前元素的前一个不在哈希集中，才有可能算出最长的序列！

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> myset;
        for(int num:nums){//先把所有的数都塞到哈希集里面
            myset.insert(num);
        }
        int res = 0;
        for(auto& num:myset){//遍历哈希集
            if(!myset.count(num-1)){//如果这个数的前一个数没记录，那我们就拿这个数当起点
                int current = num;//起点
                int currentstreak = 1;//当前的长度，包括起点
                while(myset.count(current+1)){//如果当前数的后一个存在
                    current += 1;//更新当前数
                    currentstreak += 1;//更新长度
                }
                res = max(res,currentstreak);//当以num为起点的最长连续序列结束时，更新最大长度！
            }
        }
        return res;
    }
};

最长递增子序列

  求什么子序列的问题经常能跟动态规划扯上关系。
  

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if(nums.empty()) return 0;
        vector<int> dp(nums.size(),1);
        int ans = 1;
        for(int i=0;i<nums.size();i++){
            for(int j=0;j<i;j++){//遍历每个元素的前面所有元素
                if(nums[i]>nums[j]){//如果前面某个元素比当前的小
                    dp[i] = max(dp[i],dp[j]+1);//要更新，当前值与某个值+1取最大
                }//等于是一直在算最大
            }
            ans = max(ans,dp[i]);
        }
        return ans;
    }
};

有效三角形的个数

给定一个包含非负整数的数组，你的任务是统计其中可以组成三角形三条边的三元组个数。
  暴力的不要，我们用双指针！

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n = nums.size();
        int res = 0;
        for(int i = n-1;i>=2;i--){//倒着遍历，就是为了固定最长的一条边！
            int left = 0,right = i-1;//对该边前面的区域使用双指针
            while(left<right){
                if(nums[left]+nums[right]>nums[i]){//如果两个短边之和大于第三边
                    res += right-left;//那么这个区间里面的边+right肯定都可，都算上
                    right--;//收缩right
                }else{
                    left++;//小于第三边做不成啊 增大left!
                }
            }
        }
        return res;
    }
};

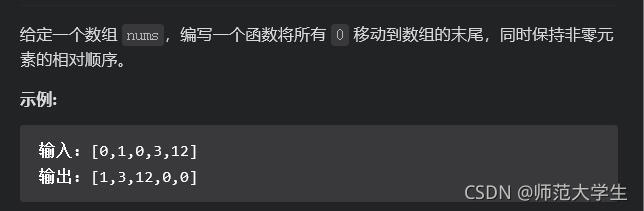
移动零

  一般遇到原地修改的问题我们可以用双指针，不过这个题我们可以稍微把双指针的用法简化一下，我们用双指针的方法去覆盖掉是0的值，最后再补上0。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int point=0;
        for(int i=0;i<nums.size();i++){
            if(nums[i]!=0){//使用快慢指针
                nums[point]=nums[i];//有点像那道：数组去重复元素
                point++;
            }
        }
        for(int i=point;i<nums.size();i++){//最后把0补上
            nums[i]=0;
        }
    }
};

搜索插入位置

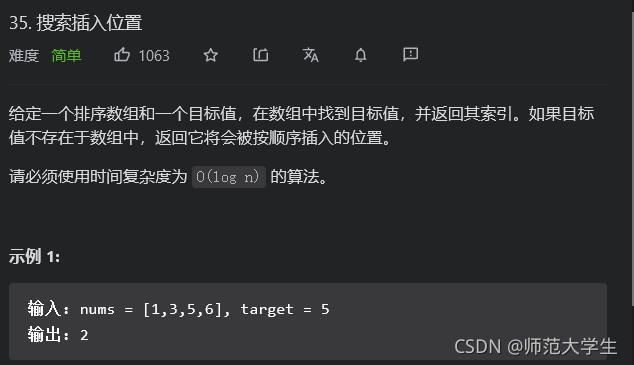  非常经典之二分查找问题。
  这里我们区分一下二分查找的两个情况，一种是左闭右闭情况下的查找，一种是左闭右开的查找。
  我们先说一下左闭右开下的代码。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(nums.empty()) return 0;
        int left=0;
        int right=nums.size();//因为是左闭右开，所以右边的初始值是n，不是n-1！
        while(left<right){//右边是开区间，所以left不可能超过right！
            int mid=left+(right-left)/2;
            if(nums[mid]<target){//因为是闭区间，left包含在内，要除去，所以令left = mid+1
                left=mid+1;
            }
            else if(nums[mid]>target){//因为是开区间，right不包含在内，所以令right = mid
                right=mid;
            }
            else{//要是有相等的就好说了
                return mid;
            }
        }
        return right;//我们可以这样认为，因为right能达到下标0和n，所以我们返回right！
    }
};

  我们再说一下左闭右闭的代码

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(nums.empty()) return 0;
        int left=0;
        int right=nums.size()-1;//因为right可以取到，所以必须是n-1
        while(left<=right){//左右都闭，所以left==right时照样可以搜
            int mid=left+(right-left)/2;
            if(nums[mid]<target){//因为是闭区间，所以left需要剔除
                left=mid+1;
            }
            else if(nums[mid]>target){//因为是闭区间，所以right需要剔除
                right=mid-1;
            }
            else{//要是相等就好说了
                return mid;
            }
        }
        return left;//可以这样想，只有left能够达到下标0和n，所以我们返回left！
    }
};

目标和

  一看是个排列问题，我们可以用到回溯思想或者深度搜索思想。
  实际上这个题还可以进一步抽象，也就是找到一个正子集和一个负子集，如果相加之和为目标就ok了。
  我们就可以通过dfs来求正子集和负子集！

class Solution {
public:
    //用pos代表下标，用于控制何时结束和给子集更新值
    //用cur记录当前的值
    int dfs(vector<int>& nums,int S,int pos,int cur){
        if(pos == nums.size()){
            return cur == S?1:0;//如果正好等于目标就返回1
        }
        int minus = dfs(nums,S,pos+1,cur-nums[pos]);//负子集计算
        int add = dfs(nums,S,pos+1,cur+nums[pos]);//正子集计算
        return add + minus;
    }

    int findTargetSumWays(vector<int>& nums, int S) {
        return dfs(nums,S,0,0);
    }
};

乘积最大子数组

  这道题看上去是不是很像“和最大的子数组”？只不过这里计算的是乘积最大，本质上都可以用贪心思想去解决。
  我们设定一个局部最大值，不断更新局部最大值并记录在全局最大值就好了。

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int max = INT_MIN;
        int imax = 1;//一开始设为1
        for(int i=0;i<nums.size();i++){
            imax = max(nums[i]*imax,nums[i]);//比较局部最大值与该元素的乘积 与 该元素本身，取最大更新，就是贪心思想！
            max = max(max,imax);//并记录最大值
        }
        return max;
    }
};

  由于该题目中有负数，所以不能这样计算。
  我们可以双向遍历，来解决这个问题，也是贪心的思想。

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int ans = INT_MIN;
        int count = 0;//双向遍历更新最大值！
        for(int i=0;i<nums.size();i++){
            if(count==0){//如果搞成0了就重新算起
                count = nums[i];
            }else{//只要不是0就直接乘，反正最大值我们随时记着
                count *= nums[i];
            }
            ans = max(count,ans);
        }
        //反向遍历一次，同样操作！
        count = 0;
        for(int i = nums.size()-1;i>=0;i--){
            if(count==0){
                count = nums[i];
            }else{
                count *= nums[i];
            }
            ans = max(count,ans);
        }
        return ans;
    }
};

砖墙

  这个题猛一看一脸懵逼，我们需要抽象化这个问题，而不是真的去穿墙。
  这个问题的抽象化其实是：在墙的长度中找到一个点，该点上有最多的砖缝，选择这条路就可以穿过最少的砖头了！
  我们可以用哈希表去存储每个点上砖缝数量，并随时更新一点上的砖缝最大值即可！

class Solution {
public:
    int leastBricks(vector<vector<int>>& wall) {
        if(wall.empty()) return 0;
        unordered_map<int,int> mymap;//建立哈希表 存储在某个距离上的砖缝数量
        int maxnum = 0;
        for(auto &walline:wall){//遍历每一层砖
            int distance = 0;
            for(int i=0;i<walline.size()-1;i++){//将每一层的砖缝位置记录在哈希表 并累加计算
                distance += walline[i];//注意墙缝的最后一个元素不要去计算，因为到头了肯定是缝，不考虑的
                mymap[distance]++;
                maxnum = max(maxnum,mymap[distance]);//随时更新
            }
        }
        return wall.size() - maxnum;
    }
};