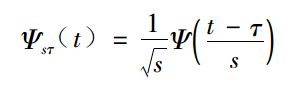类EMD的“信号分解方法”及MATLAB实现(第八篇)——离散小波变换DWT(小波分解)
在之前的系列文章里,我们介绍了EEMD、CEEMD、CEEMDAN、VMD、ICEEMDAN、LMD、EWT,我们继续补完该系列。
今天要讲到的是小波分解,通常也就是指离散小波变换(Discrete Wavelet Transform, DWT)。在网上有一些介绍该方法的文章,但是总感觉不够通俗或不够透彻,希望读完这篇能让你有所收获。
一、从小波分析到小波分解
小波分析是一种时频域分析方法,该方法兼顾了信号在时域和频域的信息。知乎上有一篇文章对小波分析的理解进行了生动的讲解,建议对小波分析概念不熟的同学先看一下。咚懂咚懂咚:能不能通俗的讲解下傅立叶分析和小波分析之间的关系?这篇文章中最后给出的小波变换的结果是这样的:
图1 连续小波变换
看起来十分厉害,不过同时会发现两个问题:运算量很大;只有数值解,没有解析解。上述这种小波分析方法叫连续小波变换(continuous wavelet transform, CWT)。
为了减少变换运算量,去除不必要的重复的系数,实际中使用的通常是离散小波变换(discrete wavelet transform, DWT)。
这里的“离散”指的是什么呢?
让我们先回到小波基波(也叫母小波)的表达式:
其中s是尺度参数,表征频率;t是位移参数,表征时间。这部分在答友的连接里也提到了。再看上一张图,xy坐标分别是SCALE和TRANSLATION,也就是s和t,他们在连续小波变换中是连续的。
所以,在离散小波变换中,“离散”的就是参数s和t。此时小波表达式写为:
j和k都是整数,通常取s0=2,τ0=1。
可以看出,随着j取值的递增,我们可以得到一串不同的小波(子小波,也叫女儿小波...)。这些子小波的尺度参数以2的j次方的形式增长。当使用这一系列的子小波,对一个连续函数进行离散分析时,我们所获得的是一组小波分析的系数,这个分析过程称为小波系列分解。
上边说道,尺度参数表征的是频率,在子小波中尺度参数以2的倍数增长(即小波的“长度”被“拉长”了2倍),那么子小波对应能检测到的频率值也会以1/2的倍数缩小。母小波所对应的频谱位于频率谱的高端,具有最大的频率谱范围- 而其他的子小波的频率谱则依次向频谱图的低频端移动,同时它们所覆盖的频率谱范围也相应地递减。在理想的情况下,所有的滤波器应该首尾相接互相覆盖。
图2 不同尺度的子小波在小波频率谱上的覆盖
是的,每个子小波就相当于一个滤波器,离散小波变换的过程就是逐级滤波的过程。
具体流程是怎样的呢?
用一句话描述就是:一组离散信号通过一系列的低通和高通滤波器,分别可以得到近似信号(用字母A表示)和细节信号(用字母D表示)。
用一张图描述就是:
图3 LP为低通滤波器,HP为高通滤波器,B为带宽,2B为2倍带宽
用一个例子来描述就是:
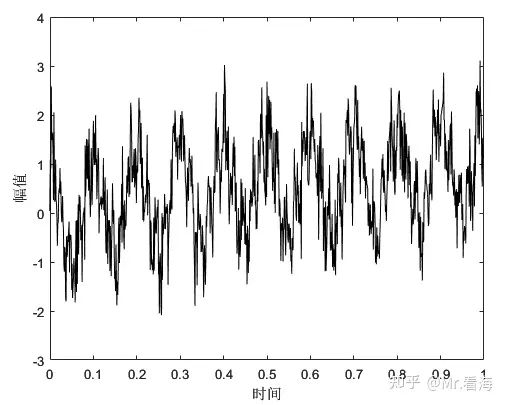
这段合成信号是由多个成分叠加而成的:一个10 Hz的低频正弦波和一个振幅为0.5的50 Hz高频正弦波,这两者代表信号的周期性成分。同时,信号中还包括了一个线性趋势项,表示信号的非周期性变化。除此之外,信号还叠加了标准差为0.5的高斯白噪声,为信号添加了随机性。这里使用了 dB4(第4级Daubechies小波)作为去除噪音操作的母小波。
原始信号
一阶小波分解的结果为:
一阶小波分解的近似信号(低通结果)
一阶小波分解的细节信号(高通结果)
二阶小波分解的结果为(即对A1信号做分解):
二阶小波分解的近似信号(低通结果)
二阶小波分解的细节信号(高通结果)
三阶小波分解的结果为(即对A2信号做分解):
三阶小波分解的近似信号(低通结果)
三阶小波分解的细节信号(高通结果)
四阶小波分解的结果为(即对A3信号做分解):
四阶小波分解的近似信号(低通结果)
四阶小波分解的近似信号(低通结果)
至此我们已经能够得到较好的低通滤波结果了。可以看到原始信号被逐级的,无遗漏地进行了高、低通滤波,且越接近低频分段越细,几乎想要哪个频段的特征都能得到,因而这个方法有个霸气的名字,叫filter banks。
小波分解的多尺度可以类比为我们使用不同的“放大镜”去观察一个物体。想象一下你手里有一张非常复杂的画,画面上有大的物体,如山脉、树木,但也有非常细小的细节,如叶子上的纹理或昆虫的触角。
粗尺度(低分辨率):当你使用低倍的放大镜(或者站得很远)去看这幅画时,你可以看到大的物体,如山脉和树木,但可能看不到细小的纹理或昆虫。 在小波分解中,这就像我们查看信号的低频部分,捕获其主要的、宽泛的特征。
细尺度(高分辨率):现在,如果你换一个高倍的放大镜(或者走近一些)去看同一幅画,你可能会失去对整体的感知,但可以清晰地看到叶子上的纹理或昆虫的触角等细节。 在小波分解中,这就像我们查看信号的高频部分,捕获其细节和快速的变化。
小波分解的美妙之处在于,它同时提供了多个尺度的视角,让我们既可以看到信号的整体特征,又可以看到其细节。这就像我们可以同时拥有多个不同倍率的放大镜,让我们在需要的时候选择合适的一个来观察画面。
二、小波分解更深一步的理解
我们先看一下下边这张图:
小波分解中的c与l
乍一看这张图与图3比较相像,不过仔细看下边的两个方框,即左侧分别标识了c和l的位置。
(一)关于小波分解系数
c的那一行是指的就是小波分解的向量。需要注意这个向量并不是上边几张图里的近似信号和细节信号,这里边存储的是小波分解的系数。小波系数是没有量纲单位的结果,需要经过重构这些系数得到实际有量纲的信号。
在我们之前讲过的小波阈值去噪方法就是针对这些小波系数,c这行的每个独立的方框(比如cA3)都可以重构到时域成为对应的滤波后的信号,也可以几个方框共同重构,这就是小波分解分量的筛选重构过程,这个过程是有实际工程应用意义的,比如可以实现滤波。
(二)小波分解和“其他类EMD分解方法”的区别
这里指的“其他类EMD方法”包括了EMD、EEMD、CEEMD、CEEMDAN、ICEEMDAN等。
小波分解与EMD分解最大的不同是源于分解机理的。
小波分解的分解结构是有包含关系的,每一层级的近似信号都要再分解为下一级的近似信号和细节信号,(这也直接导致在信号重构时不是那么随意),下图是一个典型信号的分解结果,我用红色箭头标出了其包含关系。
主要低频信号出现在每一个近似信号里
EMD通过连续地提取信号的局部极值,然后求解其上下包络,进而得到IMFs。这些IMFs是并列的关系,可以直接对选定的分量进行相加来实现重构,这种操作就比较直观了。
每个IMF分量都是由原始信号直接分解而来
那么这种分解机理的区别,会带来分解效果和应用上的什么不同呢?
我认为有以下几点:
- 上边讲到小波分解方法是多尺度的,高频分量在多个层级上被逐步细化剥离开来,让我们可以用更精准的手术刀切割出特征信号段,这是EMD所不具备的特点。
- EMD可能会受到模态混叠的影响,导致不同模式的信号成分被混在一起;小波分解方法不同层级覆盖的频率范围不同,模态混叠现象会大大减少。
- EMD的分解阶数是自适应的,换句话说无法人为干预;小波分解的分解层数是可以指定的,这方面灵活性更强。
三、小波分解DWT的MATLAB代码实现
小波分解的代码在网上可以找到一些,但是用起来不太趁手。
按照“类EMD”系列的代码的统一风格,笔者进行了封装,封装后的函数有三个,分别用于实现绘制小波分解图、小波分解各分量及频谱对应图,以及重构信号并绘制信号重构图。
(一)生成仿真信号
%% 1.生成仿真信号
Fs = 1000; % 采样频率
t = 0:1/Fs:1-1/Fs; % 时间向量
% 创建一个合成信号:包含不同频率的正弦波、趋势和噪声
signal = cos(2*pi*10*t) + 0.5*sin(2*pi*50*t) + t + 0.5*randn(size(t));
figure('color','white')
plot(t,signal,'k');xlabel('时间');ylabel('幅值') %绘制原始信号待分解的原始信号
(二)小波分解图
%% 2.绘制DWT分解图
waveletType = 'db4'; %小波名称,可选范围参考这里:https://ww2.mathworks.cn/help/wavelet/ref/wfilters.html?searchHighlight=wname&s_tid=srchtitle_wname_2#d123e130597
decompositionLevel = 4; %小波分解水平,正整数
[a,d] = pDWT(signal, decompositionLevel, waveletType); % 调用函数进行分解和画图只需要设置小波名称和小波分解水平,然后调用pDWT函数即可(函数获取方法见文末)
此时可以画出如下图:
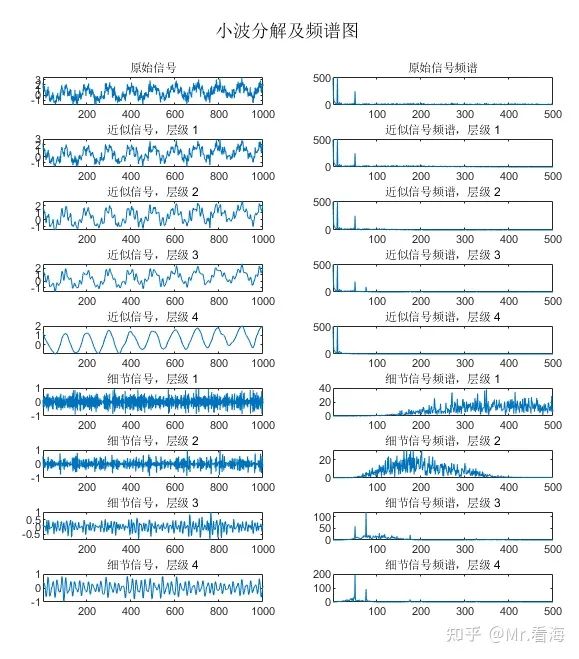
(三)小波分解及频谱图
%% 3.绘制DWT分解图及频谱图
waveletType = 'db4'; %小波名称,可选范围参考这里:https://ww2.mathworks.cn/help/wavelet/ref/wfilters.html?searchHighlight=wname&s_tid=srchtitle_wname_2#d123e130597
decompositionLevel = 4; %小波分解水平,正整数
[a,d] = pDWTandFFT(signal, decompositionLevel, waveletType); % 调用函数进行分解和画图(及频谱图)只需要设置小波名称和小波分解水平,然后调用pDWTandFFT函数即可(函数获取方法见文末)
此时可以画出如下图:
(四)小波分解重构及画图
%% 4.重构信号并绘制DWT重构图
waveletType = 'db4'; %小波名称,可选范围参考这里:https://ww2.mathworks.cn/help/wavelet/ref/wfilters.html?searchHighlight=wname&s_tid=srchtitle_wname_2#d123e130597
decompositionLevel = 4; %小波分解水平,正整数
approxLevels = 4;%所选的近似分量
detailLevels = [3 4];%所选的细节分量
combined_signal = rDWT(signal, waveletType, decompositionLevel, approxLevels, detailLevels);为了应用小波分解结果(比如滤波),很多时候要对分解结果重构。
重构的操作相对复杂一些,一来这部分代码一不小心可能就会写错;二来重构选择分量的时候也容易出错。
对于第一个问题,我写了一个重构的封装函数(就是上边这段演示的,封装函数为rDWT),只需要选择想要重构的近似分量和细节分量就行。
对于第二个问题,大家只需要注意两个问题:1.重构选择近似分量的时候,近似分量approxLevels只能选择一个层级,比如可以让approxLevels=3或者=4,但是不能=[3,4],否则低频分量就被重构了两次,重构后的数据会超出原始数据大小;2.选择了高层级的近似分量后,就不能在选择低于他的层级的细节分量,比如如果设置了approxLevels=3,就不能再选择让detailLevels =4。
调用上述分解重构及画图函数,需要设置小波名称和小波分解水平,然后调用pDWTandFFT函数即可(函数获取方法见文末)
此时可以画出如下图:
上边提到了三个封装函数,分别是:
- pDWT(小波分解并画图的程序)
- pDWTandFFT(绘制DWT分解图及频谱图)
- rDWT(重构信号并绘制DWT重构图)
上边的测试代码和封装函数,包括工具箱都可以在公众号khscience(看海的城堡)中回复"DWT"获取,EMD、EEMD、CEEMD、CEEMDAN、ICEEMDAN、VMD以及HHT相关的程序也有,编程不易,感谢支持~关于EMD、EEMD、CEEMD、VMD和HHT的相关介绍可以看这里:
Mr.看海:这篇文章能让你明白经验模态分解(EMD)——EMD在MATLAB中的实现方法
Mr.看海:希尔伯特谱、边际谱、包络谱、瞬时频率/幅值/相位——Hilbert分析衍生方法及MATLAB实现
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第一篇)——EEMD
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第二篇)——CEEMD
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第三篇)——CEEMDAN
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第四篇)——VMD
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第五篇)——ICEEMDAN
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第六篇)——LMD
Mr.看海:类EMD的“信号分解方法”及MATLAB实现(第七篇)——EWT