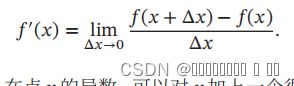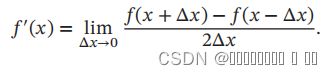第1章 实践基础——算子
声明：本内容基于百度提供的paddlepaddle框架，参考复旦大学邱锡鹏老师著作《神经网络与深度学习》（蒲公英书）与《神经网络与深度学习：案例与实践》（nndl）理解完成。（书籍源代码：源代码）
第二节：算子
2.1概念
算子（operator）是构建复杂机器学习模型的基础组件，包含一个函数
的前向函数和反向函数,即函数在机器学习代码中定义为一个算子。有了算子，我们就可以很方便地通过算子来搭建复杂的神经网络模型，而不需要手工计算梯度。
2.2简单算子
以下为一个简单的op算子：
class Op(object)：
def __init__(self):
pass
def __call__(self, inputs):
return self.forward(inputs)
# 前向函数
# 输入：张量inputs
# 输出：张量outputs
def forward(self, inputs):
# return outputs
raise NotImplementedError
# 反向函数
# 输入：最终输出对outputs的梯度outputs_grads
# 输出：最终输出对inputs的梯度inputs_grads
def backward(self, outputs_grads):
# return inputs_grads
raise NotImplementedError 在上面的算子（接口）中，forward是Op算子的前向函数，必须被子类重写，它的参数为输入对象，参数的类型和数量任意；可以直接调用模型的forward()方法进行前向执行，也可以调用__call__方法，从而执行在forward()中定义的前向计算逻辑。backward是Op算子的反向函数，也必须被子类重写，它的参数为forward输出张量的梯度outputs_grads，它的输出为forward输入张量的梯度inputs_grads。
前向计算即函数的正常计算，而向后计算为函数的求偏导的操作。
下面写一个简单的加法算子：
class add(Op):
def __init__(self):
super(add, self).__init__()
def __call__(self, x, y):
return self.forward(x, y)
def forward(self, x, y):
self.x = x
self.y = y
outputs = x + y
return outputs
def backward(self, grads):
grads_x = grads * 1
grads_y = grads * 1
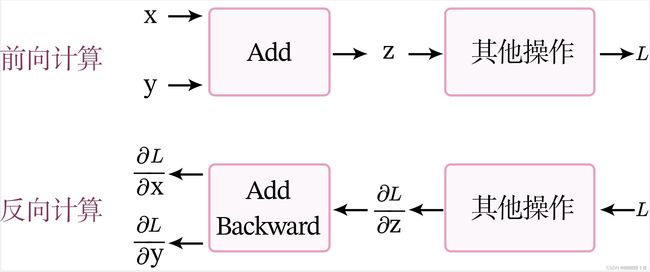
return grads_x, grads_y其中的计算过程如图（forward：前向计算，backward：反向计算。）
前向计算
当进行前向计算时，加法计算输出z=x+y。
反向计算
假设经过一个其他操作后，最终输出为L，令
,
,
。 加法算子的反向计算的输入是梯度
，输出是梯度
和
。根据链式法则，该加法算子的反向计算为
，
。
2.3常用算子
当然，在具体的机器学习操作中，算子绝对没有这么简单，下面列举几个常见算子：
Logistic激活函数算子：
class Logistic(Op):
def __init__(self):
self.inputs = None
self.outputs = None
def forward(self, inputs):
"""
:param input:inputs: shape=[N,D]
return:outputs：shape=[N,D]
"""
outputs = 1.0 / (1.0 + paddle.exp(-inputs))
self.outputs = outputs
return outputs
def backward(self, grads):
# 计算Logistic激活函数对输入的导数
outputs_grad_inputs = paddle.multiply(self.outputs, (1.0 - self.outputs))
return paddle.multiply(grads,outputs_grad_inputs)线性层linear算子：
class Linear(Op):
def __init__(self, input_size, output_size, name, weight_init=paddle.standard_normal, bias_init=paddle.zeros):
self.params = {}
self.params['W'] = weight_init(shape=[input_size, output_size])
self.params['b'] = bias_init(shape=[1, output_size])
self.inputs = None
self.grads = {}
self.name = name
def forward(self, inputs):
self.inputs = inputs
outputs = paddle.matmul(self.inputs, self.params['W']) + self.params['b']
return outputs
def backward(self, grads):
"""
:param input：损失函数对当前层输出的导数
return： 损失函数对当前层输入的导数
"""
self.grads['W'] = paddle.matmul(self.inputs.T, grads)
self.grads['b'] = paddle.sum(grads, axis=0)
# 线性层输入的梯度
return paddle.matmul(grads, self.params['W'].T)一个两层前馈神经网络算子：
# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
def __init__(self, input_size, hidden_size, output_size):
"""
：param input:
- input_size：输入维度
- hidden_size：隐藏层神经元数量
- output_size：输出维度
"""
self.fc1 = Linear(input_size, hidden_size, name="fc1")
self.act_fn1 = Logistic()
self.fc2 = Linear(hidden_size, output_size, name="fc2")
self.act_fn2 = Logistic()
def __call__(self, X):
return self.forward(X)
def forward(self, X):
"""
:param input：
- X：shape=[N,input_size], N是样本数量
return：
- a2：预测值，shape=[N,output_size]
"""
z1 = self.fc1(X)
a1 = self.act_fn1(z1)
z2 = self.fc2(a1)
a2 = self.act_fn2(z2)
return a2交叉熵损失函数算子：
# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
def __init__(self, model):
self.predicts = None
self.labels = None
self.num = None
self.model = model
def __call__(self, predicts, labels):
return self.forward(predicts, labels)
def forward(self, predicts, labels):
"""
:param input：
- predicts：预测值，shape=[N, 1]，N为样本数量
- labels：真实标签，shape=[N, 1]
return：
- 损失值：shape=[1]
"""
self.predicts = predicts
self.labels = labels
self.num = self.predicts.shape[0]
loss = -1. / self.num * (paddle.matmul(self.labels.t(), paddle.log(self.predicts))
+ paddle.matmul((1-self.labels.t()), paddle.log(1-self.predicts)))
loss = paddle.squeeze(loss, axis=1)
return loss
def backward(self):
# 计算损失函数对模型预测的导数
loss_grad_predicts = -1.0 * (self.labels / self.predicts -
(1 - self.labels) / (1 - self.predicts)) / self.num
# 梯度反向传播
self.model.backward(loss_grad_predicts)2.4微分机制
forward()函数来自动构建 backward()函数。自动微分的原理是将所有的数值计算都分解为基本的原子操作，并构建\mykey{计算图}{Computational Graph}。计算图上每个节点都是一个原子操作，保留前向和反向的计算结果，很方便通过链式法则来计算梯度。
自动计算梯度的方法可以分为以下三类：数值微分、符号微分和自动微分。
2.4.1数值微分
数值微分（Numerical Differentiation）是用数值方法来计算函数()的导数。
要计算函数 () 在点 的导数，可以对 加上一个很少的非零的扰动 Δ，通过上述定义来直接计算函数()的梯度。数值微分方法非常容易实现，但找到一个合适的扰动 Δ 却十分困难如果 Δ 过小，会引起数值计算问题，比如舍入误差；如果Δ 过大，会增加截断误差，使得导数计算不准确。因此，数值微分的实用性比较差。
)。
2.4.2符号微分
符号微分（Symbolic Differentiation）是一种基于符号计算的自动求导方法。和符号计算相对应的概念是数值计算，即将数值代入数学表示中进行计算。符号计算也叫代数计算，是指用计算机来处理带有变量的数学表达式。把表达式的变量看作符号（Symbols），一般不需要代入具体值。符号计算的输入和输出都是数学表达式，一般包括对数学表达式的化简、因式分解、微分、积分、解代数方程、求解常微分方程等运算。
比如数学表达式的化简：
输入：3 − + 2 + 1
输出：4x+1
1）编译时间较长，特别是对于循环，需要很长时间进行编译；
2）为了进行符号微分，一般需要设计一种专门的语言来表示数学表达式，并且要对变量（符号）进行预先声明；
3）很难对程序进行调试
在实际操作中无需了解其中的原理，直接在paddle平台调用backward（）函数即可.
下面用一个比较简单的例子来了解整个过程。定义两个张量a和b，并用stop_gradient属性用来设置是否传递梯度。将a的stop_gradient属性设为False，会自动为a创建一个反向张量，将b的stop_gradient属性设为True，即不会为b创建反向张量。
# 定义张量a，stop_gradient=False代表不进行梯度传导
a = paddle.to_tensor(2.0, stop_gradient=False)
# 定义张量b，stop_gradient=True代表进行梯度传导
b = paddle.to_tensor(5.0, stop_gradient=True)
c = a * b
# 自动计算反向梯度
c.backward()
print("Tensor a's grad is: {}".format(a.grad))
print("Tensor b's grad is: {}".format(b.grad))
print("Tensor c's grad is: {}".format(c.grad))out:
Tensor a's grad is: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
[5.])
Tensor b's grad is: None
Tensor c's grad is: Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False,
[1.])
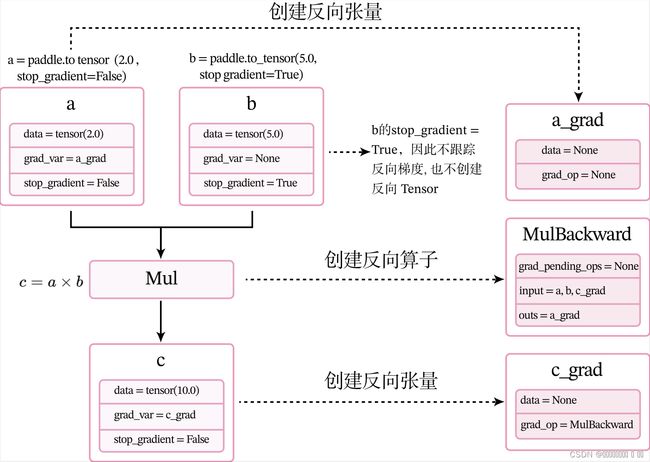
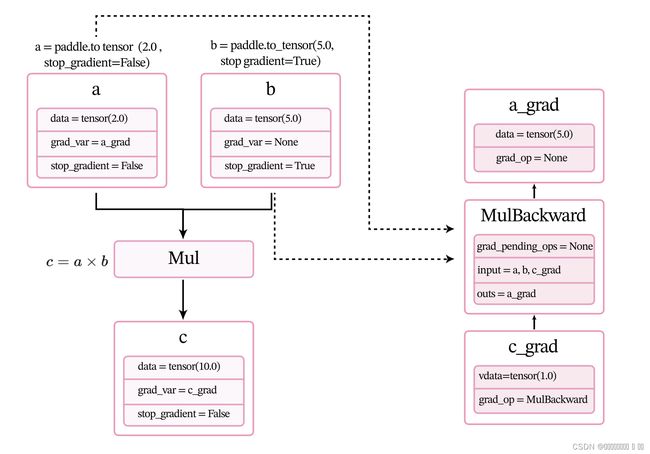
代码c.backwad被执行前，会为每个张量和算子创建相应的反向张量和反向函数。当创建张量或执行算子的前向计算时，会自动创建反向张量或反向算子。这里以上面代码中乘法为例来进行说明。
- 当创建张量a时，由于其属性
stop_gradient=False，因此会自动为a创建一个反向张量，也就是图1.8中的a_grad。由于a不依赖其它张量或算子，a_grad的grad_op为None。 - 当创建张量b时，由于其属性
stop_gradient=True，因此不会为b创建一个反向张量。 - 执行乘法c=a×bc=a\times bc=a×b 时，×\times×是一个前向算子Mul，为其构建反向算子MulBackward。由于Mul的输入是a和b，输出是c，对应反向算子
MulBackward的输入是张量c的反向张量c_grad，输出是a和b的反向张量。如果输入定义stop_gradient=True，反向张量即为None。在此例子中就是a_grad和None。 - 反向算子MulBackward中的
grad_pending_ops用于在自动构建反向网络时，明确该反向算子的下一个可执行的反向算子。可以理解为在反向计算中，该算子衔接的下一个反向算子。 - 当c通过乘法算子Mul被创建后，c会创建一个反向张量c_grad，它的
grad_op为该乘法算子的反向算子，即MulBackward。
由于此时还没有进行反向计算，因此这些反向张量和反向算子中的具体数值为空(data = None)。此时，上面代码对应的计算图状态如图
调用backward()后，执行计算图上的反向过程，即通过链式法则自动计算每个张量或算子的微分，计算过程如图1.9所示。经过自动反向梯度计算，获得c_grad和a_grad的值。
2.5预定义的算子
从零开始构建各种复杂的算子和模型是一个很复杂的过程，在开发的过程中也难以避免地会出现很多冗余代码，因此飞桨提供了基础算子和中间算子，可以便捷地实现复杂模型。
在深度学习中，大多数模型都是以各种神经网络为主，由一系列层(Layer)组成，层是模型的基础逻辑执行单元。飞桨提供了paddle.nn.Layer类来方便快速地实现自己的层和模型。模型和层都可以基于paddle.nn.Layer扩充实现，模型只是一种特殊的层。
当我们实现的算子继承paddle.nn.Layer类时，就不用再定义backward函数。飞桨的自动微分机制可以自动完成反向传播过程，让我们只关注模型构建的前向过程，不必再进行烦琐的梯度求导。
下节内容：概念基础——神经网络：人类大脑是一个可以产生意识、思想和情感的器官．受到人脑神经系统 的启发，早期的神经科学家构造了一种模仿人脑神经系统的数学模型...