【Python · PyTorch】线性代数 & 微积分

本文采用Python及PyTorch版本如下：

• Python：3.9.0

• PyTorch：2.0.1+cpu

本文为博主自用知识点提纲，无过于具体介绍，详细内容请参考其他文章。

1. 线性代数

线性代数是数学的一个分支，它的研究对象是向量、向量空间（线性空间）、线性变换及有限维的线性方程组。线性代数已被广泛地应用于自然科学和社会科学中。

• 线性（Linear）指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数。
• 非线性（Non-Linear）则相反，即量与量之间不按比例、不成直线的关系，一阶导数不为常数的函数。

1.1 基础

1.1.1 标量

在数学中，标量（Scalar）：亦称作“无向量”，只具有数值大小，没有方向，但有正负之分。

在Python中，标量即为普通的数字类型，包括int（整型）、float（浮点型）、bool（布尔型）和complex（复数）。

在数学定义中，标量等价于零阶张量；在PyTorch中也是如此，但零阶张量被表示为为仅包含一个数字的torch.Tensor类型（等价于仅包含一个元素的列表），并不完全等价于数学上的普通标量（单个数字）。

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x ** y

1.1.2 向量

在数学中，向量（Vector，亦称欧几里得向量、几何向量），指具有大小（magnitude）和方向的量，形式上表现为以原点为始点箭头指向终点的坐标。向量一般表示为带箭头的线段，表示其方向；印刷体一般为加粗体字母。

数学表示法用x∈ℝⁿ表示向量。

印刷体：
x = [ x 1 x 2 x 3 ⋮ x n ] \boldsymbol{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots\\ x_n \\ \end{bmatrix} x= ​x1​x2​x3​⋮xn​​ ​

手写体：
x → = [ x 1 x 2 x 3 ⋮ x n ] \overrightarrow{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots\\ x_n \\ \end{bmatrix} x = ​x1​x2​x3​⋮xn​​ ​

在Python中，向量可以视作由标量值组成的列表，其中的标量值被称作向量的元素（element）或分量（component）。一般可用向量表示数据集中的样本。

在数学定义中，向量等价于一阶张量，在PyTorch中也是如此。

x = torch.arange(4)
x

我们可以通过索引访问元素，获得的元素仍为PyTorch标量（即类型）。

x[3]

---

长度（维度）、形状

向量的长度与维度等价，我们可以通过Python的内置函数len来访问其长度。

len(x)

当张量为一阶张量（向量）时，我们可以通过shape属性访问其长度。

x.shape

维度之分：

• 张量：张量维度指张量的轴数（阶数）
• 向量：向量维度指元素的数量（长度）

1.1.3 矩阵

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。

在Python与数学中，矩阵同样代表二阶张量，以及向量的向量。

数学表示法用A∈ℝ^m×n来表示矩阵A，即用大写字母来表示矩阵，其中每个元素a_ij属于第i行第j列。

A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} A= ​a11​a21​⋮am1​​a12​a22​⋮am2​​⋯⋯⋱⋯​a1n​a2n​⋮amn​​ ​

A的形状为(m,n)或m×n，当m=n时，其被称作方阵（Square Matrix）。

我们可以通过调用函数创建一个5×4的矩阵。

A = torch.arange(20).reshape(5, 4)
A

与向量相同，我们可以通过索引访问元素，获得的元素仍为PyTorch标量（即类型）。

A[3, 3]

1.1.3.1 迹

迹（trace）运算是方阵对角元素的和：
$$Tr(A)=\sum _i{A}_{i,i}$$
代码如下：

D = torch.arange(16).reshape(4,4)
D.trace()

在PyTorch中，非方阵迹计算规则如下：

代码如下：

B = torch.arange(20).reshape(4,5)
C = torch.arange(20).reshape(5,4)
B, B.trace(), C, C.trace()

1.1.3.2 转置矩阵

当交换矩阵的行、列时，结果称为矩阵的转置（transpose），一般使用$A^T$表示矩阵$A$的转置。

A T = [ a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a m n ] A^T = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{bmatrix} AT= ​a11​a12​⋮a1n​​a21​a22​⋮a2n​​⋯⋯⋱⋯​am1​am2​⋮amn​​ ​

可以通过如下代码访问其转置。

A.T

当$A=A^T$时，将$A$矩阵称为对称矩阵（Systematic Matrix）。

1.1.3.3 特征值

特征值：指设$A$是n阶方阵，如果存在数m和非零n维列向量x，使得$Ax=\lambda x$成立，则称λ是$A$的一个特征值（characteristic value）或本征值（eigenvalue）。特征值分解可对满秩方阵进行分解。

具体内容见：特征值分解

1.1.3.4 奇异值

奇异值是矩阵里的概念，一般通过奇异值分解定理求得。设$A$为m*n阶矩阵，q=min(m,n)，$A{A}^T$的q个非负特征值的算术平方根叫作A的奇异值。奇异值分解是线性代数和矩阵论中一种重要的矩阵分解法，适用于信号处理和统计学等领域。

具体内容见：奇异值分解

1.1.3.5 逆矩阵

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=I ，则称方阵A可逆，并称方阵B是A的逆矩阵。
$$\begin{gathered} AB=BA=I \\ {A}^T=B \end{gathered}$$
求逆矩阵代码如下：

# 矩阵求逆一般建议使用double或float浮点型，否则无法表示元素为小数的逆矩阵
F = torch.tensor([[1., 2, 3], [0, 4, 5], [0, 0, 6]])
F.inverse()

1.1.3.6 Moore-Penrose伪逆

对于非方阵，其逆矩阵没有定义，但我们希望通过$A\in {\mathbb{R}}^{m\times n}$的左逆$B$求解线性方程：
$$Ax=y$$
即：
$$x=By$$
Moore-Penrose伪逆（Moore-Penrose广义逆）定义如下：
$$A^{+}=\underset{\alpha \to 0}{\lim }(A^{T}A+\alpha I{)}^{-1}{A}^T=V{D}^{+}{U}^T$$

其中，矩阵$U$、$D$和$V$是矩阵$A$的奇异值分解后得到的矩阵。对角矩阵$D$的伪逆$D^{+}$是其非零元素取倒数再转置得到的。

对于矩阵$A\in {\mathbb{R}}^{m\times n}$：

• 当$m＜n$时（行数＜列数），方程可能有多个解，$\mathbf{x}=A^{+}y$是所有可行解中L2范数$||x|{|}_2$最小的解。
• 当$m＞n$时（列数＜行数），方程可能没有解，$\mathbf{x}=A^{+}y$可使得$Ax$和$y$的L2距离$||Ax-y|{|}_2$最小。

1.1.4 张量

张量是一个更为一般的定义，其用特殊字体的大写字母表示（$\text{X}$），低阶张量与上述三种量的等价关系如下：

• 零阶张量：标量（Scalar）

• 一阶张量：向量（Vector）

• 二阶张量：矩阵（Matrix）

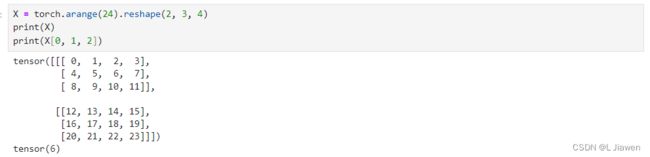
我们同样可以使用类似的方式创建高阶张量，并通过索引访问其中的元素，获得的元素仍为PyTorch标量（即类型）。

X = torch.arange(24).reshape(2, 3, 4)
print(X)
print(X[0, 1, 2])

1.2 向量空间

向量空间亦称线性空间，它是线性代数的中心内容和基本概念之一。

设V是一个非空集合，P是一个域。若：

1.在V中定义了一种运算，称为加法，即对V中任意两个元素α与β都按某一法则对应于V内惟一确定的一个元素α+β，称为α与β的和。

2.在P与V的元素间定义了一种运算，称为数乘（亦称数量乘法），即对V中任意元素α和P中任意元素k，都按某一法则对应V内惟一确定的一个元素kα，称为k与α的积。

3.加法与纯量乘法满足以下条件：

（1）α+β=β+α，对任意α,β∈V.

（2）α+(β+γ)=(α+β)+γ，对任意α,β,γ∈V.

（3）存在一个元素0∈V，对一切α∈V有α+0=α，元素0称为V的零元.

（4）对任一α∈V，都存在β∈V使α+β=0，β称为α的负元素，记为-α.

（5）对P中单位元1，有1α=α(α∈V).

（6）对任意k,l∈P，α∈V有(kl)α=k(lα).

（7）对任意k,l∈P，α∈V有(k+l)α=kα+lα.

（8）对任意k∈P，α，β∈V有k(α+β)=kα+kβ.

则称V为域P上的一个线性空间，或向量空间。

其中，V中元素称为向量，V的零元称为零向量，P称为线性空间的基域。
当P是实数域时，V称为实线性空间；当P是复数域时，V称为复线性空间。

1.3 运算

1.3.1 加 & 减

任意阶张量均可与自身形状相同的张量相加减。若与单一数字相加减，将为张量内所有元素加减对应数字（等同于张量与由对应数字组成、与其形状、大小相同的张量相加减）

标量：

# 标量
a = torch.tensor(1)
b = torch.tensor(2)
a + b, a + 1

向量：

# 向量
e = torch.tensor([1, 2, 3])
f = torch.tensor([2, 3, 4])
e + f, e + 1 

矩阵：

# 矩阵
A = torch.arange(20).reshape(4, 5)
B = torch.arange(12, 20 + 12).reshape(4, 5)
A + B, A + 1

高阶张量：

# 高阶张量
X = torch.arange(24).reshape(2 ,3, 4)
Y = torch.arange(12 , 24 + 12).reshape(2 ,3, 4)
X + Y, X + Y

1.3.2 内积 & 点积

1.3.2.1 内积

内积（Inner Product）： 亦称数量积（dot product; scalar product），是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。

假设有两向量$\mathbf{a}$, $\mathbf{b}$，则其内积表示如下：
$$⟨\mathbf{a},\mathbf{b}⟩$$

除此之外，还有 内积空间 的定义，有兴趣的读者可以自行查阅资料了解，这里不过多叙述。

计算向量内积的代码如下：

a = torch.tensor([1., 2., 3.])
b = torch.tensor([4., 5., 6.])
a.inner(b)

1.3.2.1 点积

点积（Dot Product）：内积的一种特殊形式，即欧几里得空间内积的定义。

假设有两向量$\mathbf{a}$, $\mathbf{b}$，则其点积表示如下：
$$\mathbf{a}\cdot \mathbf{b}=a_1\ast b_1+a_2\ast b_2+\cdots +a_n\ast b_n=\sum _{i=1}^n{a}_i\ast b_i$$

计算向量点积的代码如下：

a = torch.tensor([1., 2., 3.])
b = torch.tensor([4., 5., 6.])
a.dot(b)

1.3.3 外积 & 克罗内克积

克罗内克积（Kronecker product）：张量积的特殊形式

• 克罗内克积是两个任意大小的矩阵间的运算，结果仍为一个矩阵（数学符号$\otimes$，精确表达${\otimes }_k$）

我们以矩阵为例，用数学符号表示其计算过程：
A m × n ⊗ B p × q = [ a 11 B ⋯ a m 1 B ⋮ ⋱ ⋮ a 1 n B ⋯ a m n B ] = [ a 11 b 11 a 11 b 12 ⋯ a 11 b 1 q ⋯ ⋯ a 1 n b 11 a 1 n b 12 ⋯ a 1 n b 1 q a 11 b 11 a 11 b 12 ⋯ a 11 b 1 q ⋯ ⋯ a 1 n b 11 a 1 n b 12 ⋯ a 1 n b 1 q ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ ⋱ ⋮ a 11 b p 1 a 11 b p 2 ⋯ a 11 b p q ⋯ ⋯ a 1 n b p 1 a 1 n b p 2 ⋯ a 1 n b p q ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ ⋮ ⋮ a m 1 b 11 a m 1 b 12 ⋯ a m 1 b 1 q ⋯ ⋯ a m n b 11 a m n b 12 ⋯ a m n b 1 q a m 1 b 21 a m 1 b 22 ⋯ a m 1 b 2 q ⋯ ⋯ a m n b 21 a m n b 22 ⋯ a m n b 2 q ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ ⋱ ⋮ a m 1 b p 1 a m 1 b p 2 ⋯ a m 1 b p q ⋯ ⋯ a m n b p 1 a m n b p 2 ⋯ a m n b p q ] A_{m×n} \otimes B_{p×q} = \begin{bmatrix} a_{11}B & \cdots & a_{m1}B \\ \vdots & \ddots & \vdots \\ a_{1n}B & \cdots & a_{mn}B \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & \cdots & a_{11}b_{1q}& \cdots & \cdots & a_{1n}b_{11} & a_{1n}b_{12} & \cdots & a_{1n}b_{1q} \\ a_{11}b_{11} & a_{11}b_{12} & \cdots & a_{11}b_{1q}& \cdots & \cdots & a_{1n}b_{11} & a_{1n}b_{12} & \cdots & a_{1n}b_{1q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{11}b_{p1} & a_{11}b_{p2} & \cdots & a_{11}b_{pq}& \cdots & \cdots & a_{1n}b_{p1} & a_{1n}b_{p2} & \cdots & a_{1n}b_{pq} \\ \vdots & \vdots & \ddots & \vdots & \ddots & & \vdots & \vdots & & \vdots \\ \vdots & \vdots & \ddots & \vdots & & \ddots & \vdots & \vdots & & \vdots \\ a_{m1}b_{11} & a_{m1}b_{12} & \cdots & a_{m1}b_{1q}& \cdots & \cdots & a_{mn}b_{11} & a_{mn}b_{12} & \cdots & a_{mn}b_{1q} \\ a_{m1}b_{21} & a_{m1}b_{22} & \cdots & a_{m1}b_{2q}& \cdots & \cdots & a_{mn}b_{21} & a_{mn}b_{22} & \cdots & a_{mn}b_{2q} \\ \vdots & \vdots & \ddots & \vdots & & & \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{p1} & a_{m1}b_{p2} & \cdots & a_{m1}b_{pq}& \cdots & \cdots & a_{mn}b_{p1} & a_{mn}b_{p2} & \cdots & a_{mn}b_{pq} \\ \end{bmatrix} Am×n​⊗Bp×q​= ​a11​B⋮a1n​B​⋯⋱⋯​am1​B⋮amn​B​ ​= ​a11​b11​a11​b11​⋮a11​bp1​⋮⋮am1​b11​am1​b21​⋮am1​bp1​​a11​b12​a11​b12​⋮a11​bp2​⋮⋮am1​b12​am1​b22​⋮am1​bp2​​⋯⋯⋱⋯⋱⋱⋯⋯⋱⋯​a11​b1q​a11​b1q​⋮a11​bpq​⋮⋮am1​b1q​am1​b2q​⋮am1​bpq​​⋯⋯⋯⋱⋯⋯⋯​⋯⋯⋯⋱⋯⋯⋯​a1n​b11​a1n​b11​⋮a1n​bp1​⋮⋮amn​b11​amn​b21​⋮amn​bp1​​a1n​b12​a1n​b12​⋮a1n​bp2​⋮⋮amn​b12​amn​b22​⋮amn​bp2​​⋯⋯⋱⋯⋯⋯⋱⋯​a1n​b1q​a1n​b1q​⋮a1n​bpq​⋮⋮amn​b1q​amn​b2q​⋮amn​bpq​​ ​

下面我们分别展示求标量、向量、矩阵、高阶张量的克罗内克积。

标量-克罗内克积：

a = torch.tensor([2])
b = torch.tensor([3])
a.kron(b)

向量-克罗内克积：

x = torch.arange(3)
y = torch.arange(2, 2 + 3)
x.kron(y)

矩阵-克罗内克积：

X = torch.arange(20).reshape(4 ,5)
Y = torch.arange(12, 12 + 20).reshape(4 ,5)
X.kron(Y)

高阶张量-克罗内克积：

U = torch.arange(24).reshape(2, 3, 4)
V = torch.arange(15, 15 + 24).reshape(2, 3, 4)
U.kron(V)

1.3.4 哈达玛积

两个张量（标量、向量、矩阵、高阶张量）的按元素乘法称为哈达玛积（Hadamard Product）（数学符号$\odot$），在代码中用*表示求哈达玛积。

我们以矩阵为例，用数学符号表示其计算过程：

A ⊙ B = [ a 11 a 21 ⋯ a m 1 a 12 a 22 ⋯ a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n ⋯ a m n ] ⊙ [ b 11 b 21 ⋯ b m 1 b 12 b 22 ⋯ b m 2 ⋮ ⋮ ⋱ ⋮ b 1 n b 2 n ⋯ b m n ] = [ a 11 ∗ b 11 a 21 ∗ b 21 ⋯ a m 1 ∗ b m 1 a 12 ∗ b 12 a 22 ∗ b 22 ⋯ a m 2 ∗ b m 2 ⋮ ⋮ ⋱ ⋮ a 1 n ∗ b 1 n a 2 n ∗ b 2 n ⋯ a m n ∗ b m n ] A \odot B = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{bmatrix} \odot \begin{bmatrix} b_{11} & b_{21} & \cdots & b_{m1} \\ b_{12} & b_{22} & \cdots & b_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ b_{1n} & b_{2n} & \cdots & b_{mn} \end{bmatrix} =\begin{bmatrix} a_{11} * b_{11} & a_{21} * b_{21} & \cdots & a_{m1} * b_{m1} \\ a_{12} * b_{12} & a_{22} * b_{22} & \cdots & a_{m2} * b_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} * b_{1n} & a_{2n} * b_{2n} & \cdots & a_{mn} * b_{mn} \end{bmatrix} A⊙B= ​a11​a12​⋮a1n​​a21​a22​⋮a2n​​⋯⋯⋱⋯​am1​am2​⋮amn​​ ​⊙ ​b11​b12​⋮b1n​​b21​b22​⋮b2n​​⋯⋯⋱⋯​bm1​bm2​⋮bmn​​ ​= ​a11​∗b11​a12​∗b12​⋮a1n​∗b1n​​a21​∗b21​a22​∗b22​⋮a2n​∗b2n​​⋯⋯⋱⋯​am1​∗bm1​am2​∗bm2​⋮amn​∗bmn​​ ​

下面我们分别展示求标量、向量、矩阵、高阶张量的哈达玛积。

标量-哈达玛积：

a = torch.tensor([2])
b = torch.tensor([3])
a * b

向量-哈达玛积：

x = torch.arange(3)
y = torch.arange(2, 2 + 3)
x * y

矩阵-哈达玛积：

X = torch.arange(20).reshape(4 ,5)
Y = torch.arange(12, 12 + 20).reshape(4 ,5)
X * Y

高阶张量-哈达玛积：

U = torch.arange(24).reshape(2, 3, 4)
V = torch.arange(15, 15 + 24).reshape(2, 3, 4)
U * V

1.3.5 矩阵乘积

矩阵乘积（Matrix Product）：$A_{m\times n}\cdot B_{n\times p}=C_{m\times p}$，即A的列数须与B的行数相等，$C_{i,j}={\sum }_{k=1}^n{A}_{i,k}{B}_{k,j}$，在代码中用符号@表示。

标量-标量 矩阵乘积 ：标量与标量乘积可用符号@表示，也可用torch.matmul()运算。

c = torch.tensor([2])
d = torch.tensor([3])
c @ d

向量-矩阵 矩阵乘积 ：
向量与矩阵乘积可用符号@表示，也可用torch.mv()或torch.matmul()运算。

区别：

• torch.mv()须确保矩阵为第一个参数，向量为第二个参数，且形状符合运算规则。
• @或torch.matmul()则无上述限制，可将两者视为普通矩阵进行运算。

e = torch.arange(4.)  # 等效于 torch.arange(4.0)
f = torch.arange(5.)
B = torch.arange(12.,20+12).reshape(4,5)
e @ B, e.matmul(B), B.mv(f)

矩阵-矩阵 矩阵乘积 ：
向量与矩阵乘积可用符号@表示，也可用torch.mm()或torch.matmul()运算。

A = torch.arange(20.).reshape(5,4)
B = torch.arange(12.,20+12).reshape(4,5)
A @ B, A.mm(B), A.matmul(B) 

1.3.6 向量-向量叉积

向量积（Cross Product），又称叉积，是一种在向量空间中向量的二元运算，其可以新产生一个与原两向量都垂直的向量。

可以用数学符号$\times$表示叉积，有时也用^表示叉积避免与字母$x$混淆。

向量积：|c|=|a×b|=|a||b|sin
即c的长度在数值上等于以a，b，夹角为θ组成的平行四边形的面积。
而c的方向垂直于a与b所决定的平面，c的指向按右手定则从a转向b来确定。（一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。）

在PyTorch中求两向量叉积的方式如下。

x = torch.tensor([1, 2, 3])
y = torch.tensor([4, 5, 6])
x.cross(y)

1.4 范数

PyTorch范数API

torch.norm(input, p='fro', dim=None, keepdim=False, out=None, dtype=None)

其中，参数释义如下：

• input：输入tensor类型的数据（张量内元素须为浮点型/复数）
• p指定的范数
  • ‘fro’：Frobenius范数，即矩阵各项元素的绝对值平方总和。
  • ‘nuc’：核范数，即矩阵奇异值之和。
  • int型：p范数。
• dim：指定计算维度，默认所有维度计算。
• keepdim：布尔型，决定是否保留dim指定维度。
• out：输出的tensor。
• dtype：指定输出的tensor的数据类型。

首先我们定义所需的向量、矩阵。

x = torch.tensor([1., 2., 3.])      # 数字加小数点创建，默认为double型
y = torch.tensor([4., 5., 6.])

"""另外两种创建方式及不同浮点类型"""
# x = torch.tensor([1, 2, 3], dtype = torch.float64)    # 指定float64
# y = torch.tensor([4, 5, 6], dtype = torch.float64)

# x = torch.FloatTensor([1, 2, 3])          # 此方式默认float32
# y = torch.FloatTensor([4, 5, 6])


A = torch.arange(12, dtype = torch.double).reshape(3, 4)
B = torch.arange(20, dtype = torch.double).reshape(4, 5)

1.4.1 向量范数（p范数）

1.4.1.1 $l_1$范数

曼哈顿范数（L1范数）：向量所有分量绝对值之和，它受异常值影响较小。

$$||\mathbf{x}|{|}_1=\sum _{i=1}^n|x_i|$$
代码如下：

x.norm(p=1)

1.4.1.2 $l_2$范数

欧几里得范数（L2范数）：向量所有分量绝对值平方和的平方根。

$$||\mathbf{x}|{|}_2=\sqrt{\sum _{i=1}^n{x}_i^2}=(\sum _{i=1}^n{x}_i^2{)}^{\frac{1}{2}}$$

代码如下：

x.norm(p=2)

1.4.1.3 $l_{\infty }$范数

切比雪夫范数（L∞范数）：向量所有分量绝对值最大值。

$$||\mathbf{x}|{|}_{\infty }=\underset{p\to \infty }{\lim }\sqrt[p]{\sum _{i=1}^n|x_i{|}^p}=\underset{p\to \infty }{\lim }(\sum _{i=1}^n|x_i{|}^p{)}^{\frac{1}{p}}=\max (|x_i|)$$

我们已经发现了距离间的规律，这些范数被统称为p范数，可用如下公式表示所有向量p范数：
$$||\mathbf{x}|{|}_p=\sqrt[p]{\sum _{i=1}^n|x_i{|}^p}=(\sum _{i=1}^n|x_i{|}^p{)}^{\frac{1}{p}}$$

• 当 p = 1 时，上式表示 曼哈顿范数
• 当 p = 2 时，上式表示 欧几里得范数
• 当 p → ∞ 时，上式表示 切比雪夫范数

1.4.2 矩阵范数

1.4.2.1 $\mathcal{F}robenius$范数

弗罗贝尼乌斯范数：类似于向量的L2范数，矩阵$X\in {\mathbb{R}}^{m\times n}$的弗罗贝尼乌斯范数是矩阵元素平方和的平方根。

$$||X|{|}_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n{x}_{ij}^2}$$
它具有向量范数的所有性质，代码如下：

# torch默认计算Frobenius范数
A.norm()

1.4.2.2 核范数

核范数：矩阵奇异值的和，可以用来衡量矩阵的稀疏性。我们可用核范数来约束模型的复杂度，防止过拟合。

$$||X|{|}_{\ast }=tr(\sqrt{X^{T}X})=||U|{|}_1$$

其中，U是A的奇异值分解（SVD）的左奇异矩阵，$||U|{|}_1$表示其L1范数，核范数非负。

该范数常被用于约束矩阵的低秩，对于稀疏性质的数据而言，其矩阵是低秩且会包含大量冗余信息，这些信息可被用于恢复数据和提取特征。

A.norm(p='nuc')

1.5 距离（向量距离）

PyTorch距离API

torch.pairwise_distance(x1, x2, p=2.0, eps=1e-6, keepdim=False)

其中，input表示输入，p表示距离类型（默认为l2距离）

1.5.1 $l_1$距离

曼哈顿距离（L1距离）：在n维空间中，两点各坐标数值差绝对值之和。
$$d_1=\sum _{i=1}^n|x_i-y_i|$$

torch.pairwise_distance(x, y, p=1)

1.5.2 $l_2$距离

欧几里得距离（L2距离）：在n维空间中，两点各坐标数值差绝对值平方和的平方根。
$$d_2=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}=(\sum _{i=1}^n{x}_i^2-y_i{)}^2{)}^{\frac{1}{2}}$$

torch.pairwise_distance(x, y, p=2)

1.5.3 $l_{\infty }$距离

切比雪夫距离（L∞距离）：在n维空间中，两点各坐标数值差绝对值的最大值。
$$d_{\infty }=\underset{p\to \infty }{\lim }\sqrt[p]{\sum _{i=1}^n|x_i-y_i{|}^p}=\underset{p\to \infty }{\lim }(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}=\max (|x_i-y_i|)$$

我们已经发现了距离间的规律，可用如下公式表示所有向量距离：
$$d_p=\sqrt[p]{\sum _{i=1}^n|x_i-y_i{|}^p}=(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}$$

• 当 p = 1 时，上式表示 曼哈顿距离
• 当 p = 2 时，上式表示 欧几里得距离
• 当 p → ∞ 时，上式表示 切比雪夫距离

1.6 余弦相似度

余弦相似度：又称为余弦相似性，是通过计算两个向量的夹角余弦值来评估他们的相似度。

$$similarity=cos(\theta )=\frac{\mathbf{a}\cdot \mathbf{b}}{||\mathbf{a}||\cdot ||\mathbf{b}||}=\frac{{\sum }_{i=1}^n{a}_i\times b_i}{\sqrt{{\sum }_{i=1}^n(a_i{)}^2}\times \sqrt{{\sum }_{i=1}^n(b_i{)}^2}}$$

PyTorch余弦相似度API

torch.cosine_similarity(x1, x2, dim=1, eps=1e-8)

代码示例如下：

a = torch.tensor([1., 2, 3])
b = torch.tensor([2., 3, 4])
# 'Tensor' object has no attribute 'cosine_similarity'
# Tensor类型对象未内置cosine_similarity方法，需按如下方式调用
torch.cosine_similarity(a, b, dim=0)

1.7 矩阵分解

矩阵分解：将矩阵拆解为数个矩阵的乘积

1.7.1 矩阵三角分解（LR / LU分解）

三角分解：最常见的一种分解方式，便于我们求原矩阵的行列式、逆矩阵等。

1.7.2 矩阵正交三角分解（QR分解）

正交三角分解：矩阵先经过正交相似变化成为Hessenberg矩阵，再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法，与此正规正交矩阵的通用符号Q有关。

1.7.3 矩阵特征值分解（EVD分解）

特征值分解：亦称谱分解（Spectral Decomposition），将矩阵分解成特征值和特征向量表示的矩阵乘法的形式。

定义：$A$是一个n×n方阵，且有n个线性无关的特征向量$q_i(i=1,...,n)$，可将$A$分解为：
$$A=Q\Lambda Q^{-1}$$
其中，Q是n×n方针，且第i列为A的特征向量$q_i$。$\Lambda$是对角矩阵，其对角线上的元素对应特征值，即${\Lambda }_{ii}={\lambda }_i$。

只有可对角化矩阵（满秩）才能作特征分解。

1.7.4 矩阵奇异值分解（SVD分解）

定义：$A$是一个m×n实矩阵，存在一个分解使得$A=U\Sigma V^T$
其中，$U$是m×m阶正交矩阵，$\Sigma $是m\times n阶非负实数对角矩阵，$V$是n×n阶正交矩阵。

奇异值分解使得非方阵也能进行分解，由于$A{A}^T$必定为实对称矩阵，对它进行特征值分解，被称作对A进行奇异值分解。

其中，$U$和$V$均为正交矩阵，$\Sigma$是对角矩阵，根据特征值分解可以得到具体说明如下：

• $U$被称为A的左奇异矩阵，其列组成的向量是方阵$A{A}_T$的特征向量，亦称$A$的左奇异向量。
• $V$被称为A的右奇异矩阵，其列组成的向量是方阵$A{A}_T$的特征向量，亦称$A$的右奇异向量。
• $\Sigma$对角线上的元素${\sigma }_{ii}$即为A的奇异值，它们等于$A{A}_T$及$A_{T}A$特征值的平方根（$\sigma =\sqrt{\lambda }$），行对应$U$的列向量，列对应$V$的列向量。

奇异值分解的代码如下：

A = torch.tensor([[1., 2., 3., 4.],[2., 3., 4., 5.],[3., 4., 5., 6.]])
A.svd()

1.8 降维

1.8.1 基础操作

1.8.1.1 求和

我们可对张量所有元素求和：

x = torch.arange(6, dtype=torch.double)
x, x.sum()

还可以指定按列/行元素求和：

A = torch.arange(20, dtype=torch.double).reshape(5, 4)

A_sum_axis0 = A.sum(axis=0)     # 将矩阵列向量求和（沿着行挨个列向量求和）
A_sum_axis1 = A.sum(axis=1)     # 将矩阵行向量求和（沿着列挨个行向量求和）
A_sum = A.sum(axis=[0, 1])      # 沿着行、列对矩阵求和，等价于对矩阵所有元素求和
A_sum_axis0, A_sum_axis1, A_sum

1.8.1.2 平均值

同样，我们可对张量所有元素求平均，也可以指定按列/行元素求平均：

A = torch.arange(20, dtype=torch.double).reshape(5, 4)

A_mean = A.mean()    # 全部元素求平均
A_mean0 = A.mean(axis=0)     # 将矩阵列向量求平均（沿着行挨个列向量求平均）
A_mean1 = A.mean(axis=1)     # 将矩阵行向量求平均（沿着列挨个行向量求平均）
A_mean, A_mean0, A_mean1

1.8.2 PCA主成分分析

PCA（principal components analysis）主成分分析，亦称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。

在统计学中，主成分分析PCA是一种简化数据集的技术。它是一个线性变换。这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。主成分分析经常用于减少数据集的维数，同时保持数据集的对方差贡献最大的特征。

1.8.3 稀疏矩阵压缩

仅存储矩阵中的非0元素，同时存储该元素所在矩阵中的行标和列标。

其中常用的有：按列压缩（CSC, Compressed sparse column）、按行压缩（CSR, Compressed sparse row）等。

2. 微积分

在深度学习中，我们“训练模型”使其变得更好，即最小化一个损失函数（loss function）。

我们“训练”模型只能将模型与我们实际见到的数据相拟合，因此可将此任务分解为两个关键问题：

• 优化（optimization）：用模型拟合观察数据的过程。
• 泛化（generalization）：指导生成有效性超出用于训练的数据集本身的模型。

2.1 导数 & 微分

假设有一个函数$f:\mathbb{R}\to \mathbb{R}$，其输入和输出都是标量。若其导数存在，则极限被定义为：
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
若$f^{\prime }(a)$存在，则称f在a处可微（differentiable）

2.2 偏导数

在深度学习中，通常需要用到多变量，我们将其思想推广到多元函数（multivariate function）

设$y=f(x_1,x_2,\cdots ,x_n)$，则y关于第i个参数x_i的偏导数（Partial Derivative）为：

$$\frac{\partial y}{\partial x_i}=\underset{h\to 0}{\lim }\frac{f(x_1,\cdots ,x_{i-1},x_i+h,x_{i+1},\cdots ,x_n)-f(x_1,\cdots ,x_i,\cdots ,x_n)}{h}$$

2.3 梯度

假设有一个函数$f:{\mathbb{R}}^n\to \mathbb{R}$，其输入是一个n维向量$\mathbf{x}=[x_1,x_2,\cdots ,x_n]$，其输出是一个标量，则函数$f(\mathbf{x})$相对于$\mathbf{x}$的梯度是一个包含n个偏导数的向量：
$${\nabla }_{x}f(\mathbf{x})=[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\cdots ,\frac{\partial f(\mathbf{x})}{\partial x_n}]$$

假设$\mathbf{x}$为n维向量，在对多元函数求微分时经常使用以下规则：

• 对于所有$A\in {\mathbb{R}}^{m\times n}$，都有${\nabla }_{x}Ax=A^T$
• 对于所有$A\in {\mathbb{R}}^{n\times m}$，都有${\nabla }_x{x}^{T}A=A$
• 对于所有$A\in {\mathbb{R}}^{n\times n}$，都有${\nabla }_x{x}^{T}Ax=(A+A^T)x$
• ${\nabla }_x||\mathbf{x}|{|}^2={\nabla }_x{\mathbf{x}}^T\mathbf{x}=2\mathbf{x}$

同样，对于任何矩阵$X$，都有${\nabla }_X||X|{|}_F^2=2X$。

---

例如，定义一个函数：
$$f(\mathbf{x})={\mathbf{k}}^{\mathbf{T}}\mathbf{x}+\mathbf{b}$$
其中：
$$\begin{gathered} k^T=[1,3,5] \\ {b}^T=[1,2,3] \end{gathered}$$
我们可采用自动微分的方式对示例这种函数求梯度，具体可参考下面两例。

2.4 Hessian矩阵

Hessian矩阵，中文译名为海森矩阵。

假设有一个函数$f:{\mathbb{R}}^n\to \mathbb{R}$，其Hessian矩阵定义如下：
H ( f ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] H(f)= \begin{bmatrix} \frac{\partial^{2} f}{\partial x_1^{2}} & \frac{\partial^{2} f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^{2} f}{\partial x_1 \partial x_n} \\ \frac{\partial^{2} f}{\partial x_2 \partial x_1} & \frac{\partial^{2} f}{\partial x_2^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_n \partial x_1} & \frac{\partial^{2} f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^{2} f}{\partial x_n^{2}} \end{bmatrix} H(f)= ​∂x12​∂2f​∂x2​∂x1​∂2f​⋮∂xn​∂x1​∂2f​​∂x1​∂x2​∂2f​∂x22​∂2f​⋮∂xn​∂x2​∂2f​​⋯⋯⋱⋯​∂x1​∂xn​∂2f​∂x2​∂xn​∂2f​⋮∂xn2​∂2f​​ ​

• 当H为正定矩阵时，则该点是极小值点
• 当H为负定矩阵时，则该点是极大值点
• 当H为不定矩阵时，则该点是非极值点
• 当H为半正定矩阵/半负定矩阵时，$f(x_1,x_2,\cdots ,x_n)$则该点是 “可疑”极值点，需结合其他方法判定。

定义一个函数：
$$f(\mathbf{x})={\mathbf{b}}^{\mathbf{T}}\mathbf{x}+\frac{1}{2}{\mathbf{x}}^{\mathbf{T}}\mathbf{Ax}$$
其中：
b T = [ 1 , 3 , 5 ] A = [ − 5 − 3 − 0.5 − 3 − 2 0 − 0.5 0 − 0.5 ] b^{T}=[1,3,5] \\ A = \begin{bmatrix} -5 & -3 & -0.5 \\ -3 & -2 & 0 \\ -0.5 & 0 & -0.5 \end{bmatrix} bT=[1,3,5]A= ​−5−3−0.5​−3−20​−0.50−0.5​ ​

本例代码采用自动微分的方式，对上述函数对上述函数原点处的Hessian矩阵进行计算：

import torch

# 函数定义
x = torch.tensor([0., 0, 0], requires_grad=True)
b = torch.tensor([1., 3, 5])
A = torch.tensor([[-5, -3, -0.5],[-3, -2, 0],[-0.5, 0, -0.5]])


def func(x):
    return b @ x + 0.5 * x @ A @ x


"""两次梯度求解Hessian矩阵"""
# 计算一阶导数,因为我们需要继续计算二阶导数,所以创建并保留计算图
grad = torch.autograd.grad(func(x), x, retain_graph=True, create_graph=True)
# 定义Print数组,为输出和进一步利用Hessian矩阵作准备
p = torch.tensor([])
for anygrad in grad[0]:  # torch.autograd.grad返回的是元组
    p = torch.cat((p, torch.autograd.grad(anygrad, x, retain_graph=True)[0]))
print(p.view(x.size()[0], -1))


"""API求解Hessian矩阵"""
print(torch.autograd.functional.hessian(func, x))

2.5 Jacobian矩阵

Jacobian矩阵，中文译名为雅可比矩阵。

假设有一个函数$\mathbf{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m$，其由多个函数组成：
f = [ f 1 ( x 1 , x 2 , ⋯   , x n ) f 2 ( x 1 , x 2 , ⋯   , x n ) ⋮ f m ( x 1 , x 2 , ⋯   , x n ) ] \boldsymbol{f} = \begin{bmatrix} f_{1}(x_1, x_2, \cdots, x_n)\\ f_{2}(x_1, x_2, \cdots, x_n)\\ \vdots \\ f_{m}(x_1, x_2, \cdots, x_n)\\ \end{bmatrix} f= ​f1​(x1​,x2​,⋯,xn​)f2​(x1​,x2​,⋯,xn​)⋮fm​(x1​,x2​,⋯,xn​)​ ​

其雅可比矩阵定义为：
J ( f ) = [ ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 ⋯ ∂ f 1 ∂ x n ∂ f 2 ∂ x 1 ∂ f 2 ∂ x 2 ⋯ ∂ f 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f n ∂ x 1 ∂ f n ∂ x 2 ⋯ ∂ f n ∂ x n ] J(\boldsymbol{f}) = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \frac{\partial f_n}{\partial x_2} & \cdots & \frac{\partial f_n}{\partial x_n} \end{bmatrix} J(f)= ​∂x1​∂f1​​∂x1​∂f2​​⋮∂x1​∂fn​​​∂x2​∂f1​​∂x2​∂f2​​⋮∂x2​∂fn​​​⋯⋯⋱⋯​∂xn​∂f1​​∂xn​∂f2​​⋮∂xn​∂fn​​​ ​

定义一个函数（$\mathbf{f}:{\mathbb{R}}^3\to {\mathbb{R}}^4$）：

f ( x ) = [ f 1 ( x 1 , x 2 , x 3 ) f 2 ( x 1 , x 2 , x 3 ) f 3 ( x 1 , x 2 , x 3 ) f 4 ( x 1 , x 2 , x 3 ) ] = [ x 1 5 x 3 4 x 2 − 2 x 3 x 3 ] \boldsymbol{f}(\boldsymbol{x})=\begin{bmatrix} f_{1}(x_1,x_2,x_3) \\ f_{2}(x_1,x_2,x_3) \\ f_{3}(x_1,x_2,x_3) \\ f_{4}(x_1,x_2,x_3) \\ \end{bmatrix} =\begin{bmatrix} x_1 \\ 5x_3 \\ 4x_2-2x_3 \\ x_3 \\ \end{bmatrix} f(x)= ​f1​(x1​,x2​,x3​)f2​(x1​,x2​,x3​)f3​(x1​,x2​,x3​)f4​(x1​,x2​,x3​)​ ​= ​x1​5x3​4x2​−2x3​x3​​ ​

import torch

# 函数定义
x = torch.tensor([1., 1, 1], requires_grad=True)
A = torch.tensor([[1.,0,0],[0,0,5],[0,4,-2],[0,0,1]])

def func(x):
    return A @ x

"""梯度重组矩阵求解Jacobian矩阵"""
jac = torch.tensor([])
# 分别计算f[i]对x的梯度，再拼接为矩阵
for j in func(x):
    jac = torch.cat((jac, torch.autograd.grad(j, x, retain_graph=True)[0]))
print(jac.view(func(x).size()[0], -1))


"""API求解Jacobian矩阵"""
print(torch.autograd.functional.jacobian(func, x))