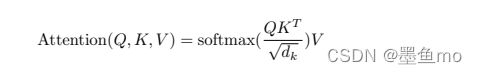Attention Is All You Need 论文笔记

2017 年，Google 机器翻译团队发表的《Attention is All You Need》中，完全抛弃了RNN和CNN等网络结构，而仅仅采用Attention机制来进行机器翻译任务，并且取得了很好的效果，注意力机制也成为了大家近期的研究热点。该论文发表在2017年的NIPS 上。

1、Attention机制

Attention用于计算“相关程度”，他考虑的是随意线索，而CNN，RNN考虑的是不随意线索。

Attention可以进行以下描述，表示为将query（Q）和key(K)-value(V)映射到输出上，输出是所有V的加权和，权重是根据query和key的相似度计算的并进行softmax归一化。

自注意机制是将输入Xi当做key,value,query(复制成三份)，来对序列抽取特征。

Transformer

首先是说之前做的工作，主流的模型还是利用CNN和RNN,且比较复杂。介绍当前模型的局限性。

RNN的两个缺陷：

1、要计算ht就要知道ht-1和当前的输出t，所以想要得到t的隐藏状态，就必须要计算ht-1的隐藏状态，这使得RNN的并行度是很差的，需要一步一步的向后计算。

2、RNN记忆过早的历史信息比较差，时序信息是一步一步往后计算的。

考虑使用CNN代替RNN来解决并行问题（CNN有多个输出通道），但是CNN也有问题，CNN对长序列难以建模。因为卷积做计算的时候，每次是看一个比较小的窗口（例如3*3的窗口），两个像素点离得比较远，那么要通过很多层卷积把两个像素点联系起来。

CNN的多个输出通道，且每个通道的是不一样的，这一点和本文中提出的Multi-Head Attention是相似的。

Model Architecture

模型采用的是Encoder-Decoder架构。（输出结构化信息比较多，适合编码器-解码器架构）

编码器会将输入序列X=(X1,,,,Xn)(如果X是一个句子，那么每个分量是一个词)映射成向量Z=（Z1,,,,Zn）.

解码器做的是一个自回归，是一个词一个词生成的，无法看到整个句子，当前的输出的输入集是上一个时刻的输出。

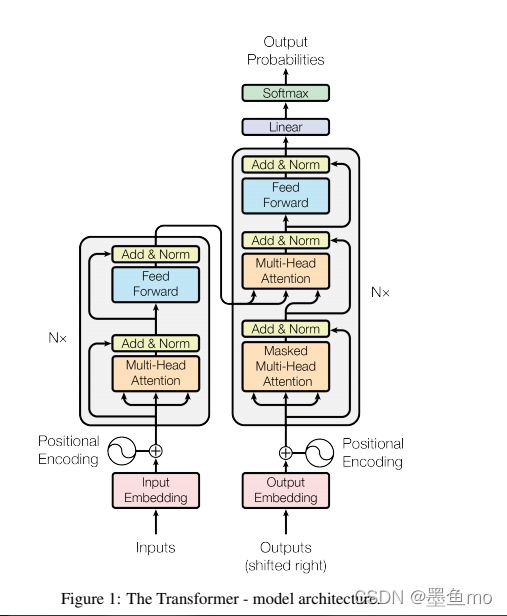
模型的整个架构如下图：

Transformer 编码器

使用了N=6完全一样的模块，每个块由两个子层组成：Multi-head self-attention和FNN（其实就是一个单隐藏层的MLP） ，对于每个子层使用了残差连接（残差连接的输入与输出维度大小要相通同），在最后使用了一个层归一化(Layernorm)，即每个子层的输出是：LayerNorm(x+Sublayer(x))

这里的为了计算方便使用统一的维度为512，（与卷积不同，卷积每经过一层，空间维度会减小，通道的维度会增加）

输入首先使用了一个词嵌入方法，使词变为向量d=512，方便计算，接着将向量加入位置编码，（在输入中加入位置信息），使得自注意力能够记忆位置信息，假设长度为n的序列X（n*d的矩阵），那么使用位置编码P（n*d），来输出X+P作为自编码输入。P的元素计算如下：

这里使用正余弦函数计算，每列的周期不一样（可以看出每个样本加的值是不一样的），这里记录的是相对位置信息（即第i个位置的信息和第i+e位置的两者的相对位置），而不是绝对位置信息。

Transformer 解码器

使用了N=6完全一样的模块，每个模块有三个子层组成：Masked multi-head self-attention、Multi-head attention和FNN(其实就是一个单隐藏层的MLP)，由于在预测时，当前时间的输出不应该看到当前时间之后的输入（当前时间之后的权重为0），所以第一个是带掩码（mask）的注意力机制。

 Layer_Norm

神经网络学习过程中的本质是为了学习数据的分布，如果不做归一化，每批次训练的数据的分布是不一样的（一般有四个步骤，计算均值、方差，归一化处理到均值为0，方差为1(减去均值，除以标准差)，变化重构）。

transformer使用的层归一化，这里可以与batch_norm做对比。

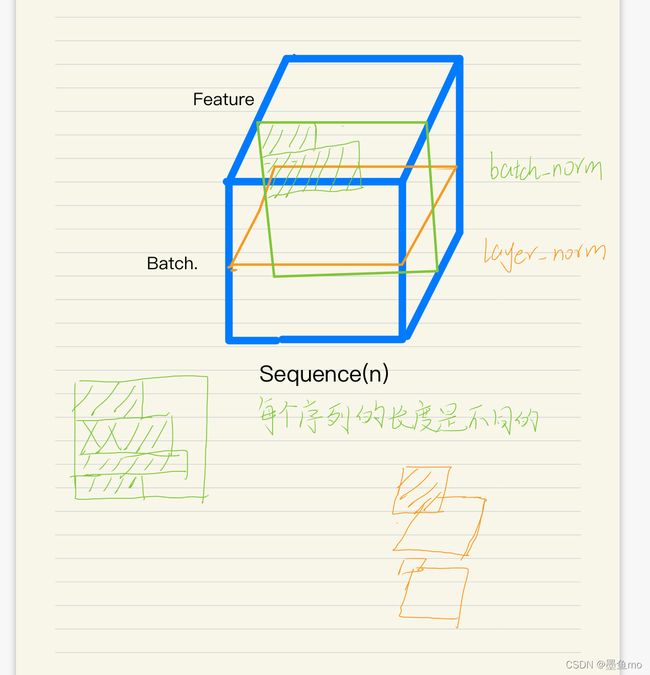
batch_norm：批量归一化对每个特征/通道元素做归一化 。

layer_norm:层归一化对每个样本的进行归一化处理，比较适合序列长度变化的NLP应用。

各种归一化操作的简单介绍

layer_norm和batch_norm的主要区别如下图，

 Attention

注意力函数是将一个query和一些key-value键值对映射成一个输出的函数，query,key,values和output是一些向量。output是values的加权和(其输出的维度与values的维度是一致的)，其中这些权重是通过计算key和query的相似度得出的。

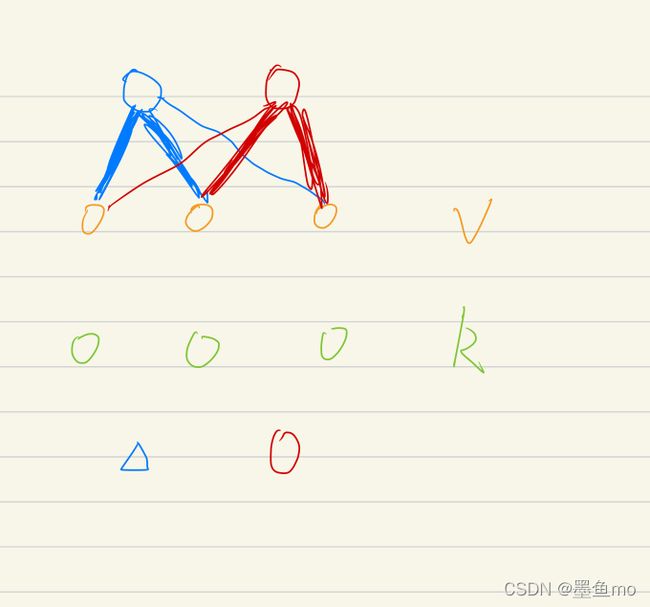
 以图为例，蓝色的Q靠近K的前两个值（与前两个K的相似度比较高），所以对应的前两个V的权重会比较大，同理红色的Q靠近后两个，后两个V对应的权重会比较大。不同的Q会导致权重分配不同，这样得到的输出也是不一样的。

Scaled Dot-Product Attention

attention的计算方法有很多，这里transformer采用的是一种比较简单的方法，内积计算相似度，

q和k的维度相同都为dk，values的维度为dv（输出也是），q,k,v都是向量，q,k采用的内积的方法计算相似度，内积越大说明相似度越高，如果内积为0，说明向量正交，没有相似度。内积为负（钝角），但经过softmax还是会在0-1之间。

如果一个一个计算那么效率会很低，一般采用矩阵的方法。

Q(n,dk), K(m,dk),V(m,dv),其注意力机制计算公式如下：

这里相似度计算采用的dot-product attention(内积法，维度要相同)，还有一种方法时additive-attention(加性法，维度可以不同)，两种方法其实差不多，但是内积法的速度更快，空间效率高。

首先做内积计算相似度，再利用softmax产生权重并把V加权求和，这里与内积法不同的是除以了根号下dk,为什么除以sqrt(dk)原因

 在dk不大的时候，开不开根号都可以，但是当维度很大时，内积的值会比较大或者比较小。当值很大的时候，相对的差距会变大，导致最大值 softmax会更加靠近于1，剩下那些值就会更加靠近于0。softmax的值会在两端，这样梯度会比较小，剃度比较小，优化起来就比较困难，就可能跑不动，transformer中的dk=512，是比较大的，所以除以根号dk是个不错的选择。

其模型如下图：

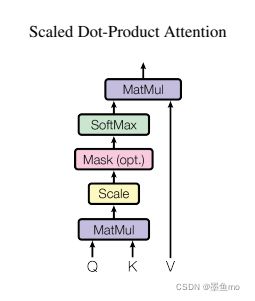这里加了一个mask，对于t时间的qt，本应该只看到k1,k2,,,,kt-1,后面的还没有，但在注意力机制，qt会看到所有的k，k1,k2,,,,kt，所以在计算当前值时，其后的值令其为一个很大的负数，这样做softmax就会变为0。

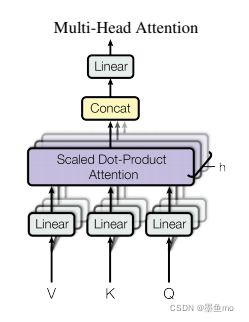
Multi-Head Attention

如果只做单一的注意力机制函数，效果不是很好，不如说把整个query，key,value线性投影到（project）到一个低维的空间，投影h次，然后再做h次注意力函数，把每个函数的输出拼接起来，再投影到原来的维度进行输出。

为什么要用多头？ 

单个的Dot-Product Attention没有什么参数可以学习，但还是希望能够学得一些东西，所以将其线性投影到低维，这个投影权重的W的矩阵是可以学习的，投影h次，会得到h个不同的模型，有点类似于CNN的多通道。可以提高并行度。

维度d=512，h=8,所以他投影到了512/8=64维上面。因为投影到了低维度，其计算成本与全维度的计算成本相似。

transformer使用了三种不同方式的multi-head attention。

编码器中的self-attention

 因为是自注意力机制，所以qkv是一样的，所以最后的输出维度与输入维度是相同的。

解码器中的self-attention

这里加了一个掩码（mask），也是为了不能知道后面的信息。

解码器中另一个attention

 这里的key、values不再是自己，而是来自编码器输出。query来自之前解码器的输出。

Feed Forward

其本身就是一个MLP,max就是一个RELU激活函数。xW1+b1是第一层，max()W2+b2是第二层。

 x是query后的输出，维度是d=512.W1会投影到2048，W2又把2048投影回了512.（即中间隐藏层扩大了四倍）。

与RNN做对比，两者的传递信息的方式不同，而语义转换的MLP基本相同。

attention是把序列中的信息抓取出来，做一次加权求和，然后放到MLP中，这里每个词用了一个MLP，其所有的MLP的权重是一样的。

RNN是上一个时刻的信息传输到下一个时刻做输入来进行信息传递。

Embedding

embedding：将输入的一个词、词语 token 映射成为一个长为 d = 512的向量。

论文中提到模型的编码器、解码器之前的 2个 embedding 共享权重。–> 训练更简单【注意这里是把英语和德语放到一个字典中了，不再分开做两个字典，所以才能共享权重】。

注意Embedding之后乘了一个sqrt(d)！

原因：权重 * sqrt(dmodel = 512) ，学 embedding 的时候，会把每一个向量的 L2 Norm 学的比较小。维度大的话，学到的一些权重值就会变小，但之后还需要加上 positional encoding（不会随着维度的增加而变化，是一个-1， 1之间的数）。

why attention

n是序列长度，d是维度。

self-attention的复杂度计算是，Q,K（n*d）两个矩阵相乘,所以复杂度为n*n*d

Sequential Operations 是指做下一步操作之前要等待多久，越小越好。

Maximum Path Length是指信息从一个点到另一个点要多久，越小越好。