动态规划:拿纸牌游戏
题目
给定一个整型数组 arr,代表数值不同的纸牌排成一条线。
玩家A 和 玩家B 依次拿走每张纸牌。
规定玩家 A 先拿,玩家B后拿,但是每个玩家每次只能拿走最左或最右的纸牌,玩家A和玩家B都绝顶聪明。
请返回最后获胜者的分数。
思路及实现
假设在 arr[l...r] 范围拿牌。 先手函数 int f(arr, l, r),后手函数int g(arr, l, r)
如果是先手姿态:
- 如果只有一张牌:
if(l == r) return arr[l]; - 如果不止一张牌:
- 如果拿走左侧的牌,那么在剩下的牌中就是后手姿态,那获得的分数就是:
arr[l] + g(arr, l + 1, r); - 如果拿走右侧的牌,那么在剩下的牌中也是后手姿态,获得的分数就是:
arr[r] + g(arr, l, r - 1); - 为了获取较大分数,就选二者中较大值,所以作为先手最后的得分是
max{arr[l] + g(arr, l + 1, r), arr[r] + g(arr, l, r - 1)}
- 如果拿走左侧的牌,那么在剩下的牌中就是后手姿态,那获得的分数就是:
如果是后手姿态:
- 如果只有一张牌,先手拿了,后手就无牌可拿:
if (l == r) return 0; - 如果不止一张牌:
- 如果先手拿走了左侧的牌,那么在剩下的牌中,后手变为先手姿态,所以得分为:
f(arr, l + 1, r); - 如果先手拿走了右侧的牌,那么在剩下的牌中,后手变为先手姿态,所以得分为:
f(arr, l, r - 1); - 而作为后手,是没有选择权的,只能对手给你结果,而对手只会给你最小值,所以最终获得的分数:
min{f(arr, l + 1, r),f(arr, l, r - 1) }
- 如果先手拿走了左侧的牌,那么在剩下的牌中,后手变为先手姿态,所以得分为:
//纯暴力的方法
public class CardsInLine {
//根据规则,返回获胜者的分数
public static int win1(int[] arr) {
if (arr == null || arr.length == 0)
return 0;
int first = f(arr, 0, arr.length - 1);
int second = g(arr, 0, arr.length - 1);
return Math.max(first, second);
}
//arr[l...r] 先手获得的最好分数返回
public static int f(int[] arr, int l, int r) {
if (l == r) return arr[l];
int p1 = arr[l] + g(arr, l + 1, r);
int p2 = arr[r] + g(arr, l, r - 1);
return Math.max(p1, p2);
}
//arr[l...r],后手获得的最好分数返回
public static int g(int[] arr, int l, int r) {
if (l == r) return 0;
int p1 = f(arr, l + 1, r); //对手拿走了l位置的数
int p2 = f(arr, l, r - 1); //对手拿走了r位置的数
return Math.min(p1, p2);
}
}
根据递归函数分析位置依赖:
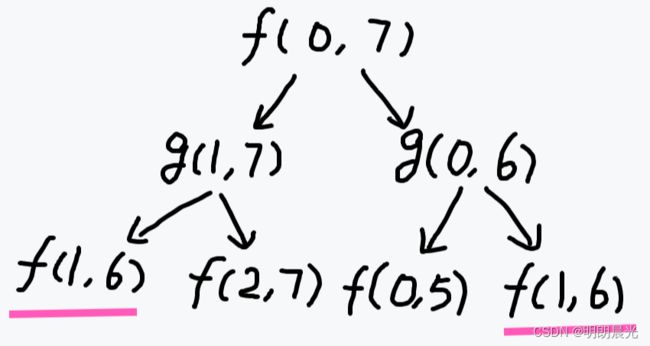
如上,出现了重复解。所以如果继续做动态规划的话,有利可图,不用将相同的过程再展开一遍了。
所以接下来,进行优化——傻缓存。
但是仔细分析 f 和 g 函数发现它们是相互依赖的,但是没关系,f 有一张表,g 有一张表,那准备两张表就行了:
public class CardsInLine {
public static int win2(int[] arr) {
if (arr == null || arr.length == 0) return 0;
int n = arr.length;
//根据可变参数l和r的范围准备两张表
int[][] fmap = new int[N][N];
int[][] gmap = new int[N][N];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
fmap[i][j] = -1;
gmap[i][j] = -1;
}
}
int first = f2(arr, 0, arr.length - 1, fmap, gmap);
int second = g2(arr, 0, arr.lenght - 1, fmap, gmap);
return Math.max(first, second);
}
//arr[l...r],先手获得的最好分数返回
public static int f2(int[] arr, int l, int r, int[][] fmap, int[][] gmap) {
if (fmap[l][r] != -1)
return fmap[l][r];
int ans = 0;
if (l == r) {
ans = arr[l];
} else {
int p1 = arr[l] + g2(arr, l + 1, r, fmap, gmap);
int p2 = arr[r] + g2(arr, l, r - 1, fmap, gmap);
ans = Math.max(p1, p2);
}
fmap[l][r] = ans;
return ans;
}
//arr[l...r],后手获得的最好分数返回
public static int g2(int[] arr, int l, int r, int[][] fmap, int[][] gmap) {
if (gmap[l][r] != -1)
return gmap[l][r];
int ans = 0;
if (l != r) {
int p1 = f2(arr, l + 1, r, fmap, gmap);
int p2 = f2(arr, l, r - 1, fmap, gmap);
ans = Math.min(p1, p2);
}
gmap[l][r] = ans;
return ans;
}
public static void main(String[] args) {
int[] arr = {5, 7, 4, 5, 8, 1, 6, 0, 3, 4, 6, 1, 7};
System.out.println(win2(arr));
}
}
接下来分析严格表依赖的动态规划。
当 l == r 时,即表中的对角线应该填充的数如下:
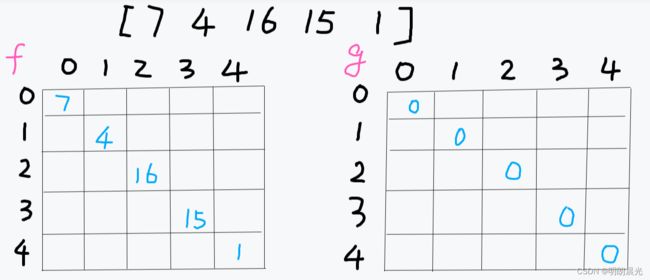
主函数中需要的就是表中 (0, n-1) 位置的值,就是图中的五角星位置:
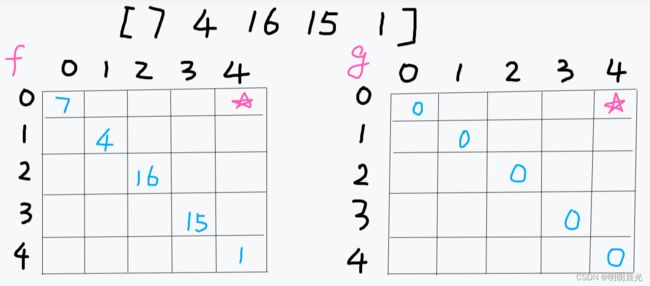
此时,已经得到了初始位置和目标位置。
因为是一个范围的左和右,所以 l <= r 这个是一定满足的,于是表中的下半部分无效:

接着分析普遍位置的依赖:f 表依赖于 g 表,那么在 f 表的有效普遍位置中在 g 表找到一个对称的位置,然后找到依赖关系。如下图所示:

同理,g 表依赖于 f 表:
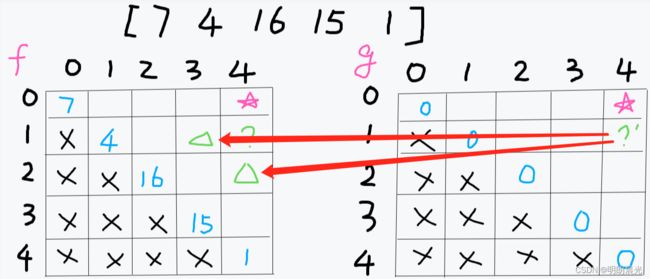
那么因为这种依赖关系,以及对角线的值已经得到了,所以能根据 f 的对角线值推出g 表的值;同理,得到了 g 表的值之后可以倒推 f 表的值。
public class CardsInLine {
public static int win3(int[] arr) {
if (arr == null || arr.length == 0) return 0;
int n = arr.length;
//根据可变参数l和r的范围准备两张表
int[][] fmap = new int[n][n];
int[][] gmap = new int[n][n];
for (int i = 0; i < n; i++) {
fmap[i][i] = arr[i]; //填充对角线的值
}
for (int startCol = 1; startCol < n; i++) {
int l = 0;
int r = startCol;
while (r < n) {
//上面推导出来的位置依赖关系
fmap[l][r] = Math.max(arr[l] + gmap[l + 1][r], arr[r] + gmap[l][r - 1]);
gmap[l][r] = Math.min(fmap[l + 1][r], fmap[l][r - 1]);
l++;
r++;
}
}
return Math.max(fmap[0][n - 1], gmap[0][n - 1]);
}
}