文献笔记|分子性质预测|Motif-based Graph Self-Supervised Learning for Molecular Property Prediction

Motif-based Graph Self-Supervised Learning for Molecular Property Prediction

题目：基于模体的图自监督学习用于分子性质预测

来源：NeurIPS 2021

单位：中国科学技术大学

挑战

然而，大多数现有的GNNs自监督预训练框架只关注节点级或图级任务。这些方法不能捕捉子图或图模体中的丰富信息。例如，官能团(分子图中经常出现的子图)通常携带有关分子性质的指示性信息。

具体来说：

1. 现有的模体挖掘技术不能直接用于获得分子图的表达基序，因为它们只依赖于子图结构的离散计数，而忽略了化学有效性[1，18]。
2. 大多数图生成技术逐节点生成图形[23，50]，这不适合我们的模体生成任务。
3. 如何协调统一多层次的自我监督预训练任务带来了新的挑战。一个简单的解决方案是按顺序进行训练前的任务，这可能会导致灾难性的遗忘，类似于持续学习[7]。

方法概括

为了应对上述挑战，本文提出了基于模体的图自监督学习和多级自监督预训练。

1. MGSSL引入了一个新颖的模体生成任务，使GNNs能够从图模体中捕获丰富的结构和语义信息。为了获得语义上有意义的基序并构建分子图的基序树，我们利用了BRICS算法[4],该算法基于化学领域的逆向合成。进一步引入两个额外的分段规则以减少模体词汇的冗余。
2. 设计了一个通用的基于模体的生成式预训练框架来逐模体生成分子图。预训练模型需要在每一步进行拓扑和属性预测，并且实现了两种特定的生成顺序(广度优先和深度优先)。
3. 为了考虑分子的多尺度规律性，我们为GNNs引入了多级自我监督预训练，其中不同SSL任务的权重由Frank-Wolfe算法自适应调整[16]。
4. 通过使用我们的方法在ZINC数据集上预训练GNNs，预训练的GNNs在各种下游基准任务上优于所有最先进的基线，证明了我们设计的有效性。

该实现可在https://github.com/zaixizhang/MGSSL.公开获得

MGSSL

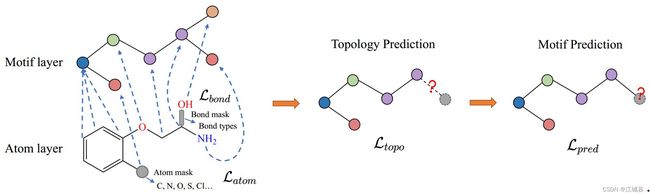
图1:基于模体的图自监督学习(MGSSL)的图示。多层次的预训练包括两层，原子层和模体层。在原子层，我们屏蔽节点/边属性，让GNNs基于相邻结构预测这些属性。在模体层，我们构建模体树并进行模体生成预训练。在每一步中，基于现有的模体和边，拓扑和模体预测迭代进行。

受化学启发的分子分割

• 给定一个分子图$G=(V,E)$，一个模体树$\mathcal{T}(G)=(\mathcal{V},\mathcal{E},\mathcal{X})$是一个连通带标签的树，其中节点集是$\mathcal{V}=\{M_1,...,M_n\}$，边集是$\mathcal{E}$。
• $\mathcal{X}$指诱导的模体词汇。每个模体$M_i=(V_i,E_i)$是$G$的一个子图。

分子分子方法应该满足以下目标：

1. 在模体树$\mathcal{T}(G)$中，所有模体$M_i$的联合应该与$G$相等。形式上，${\bigcup }_i{V}_i=V$ 且 ${\bigcup }_i{E}_i\bigcup \mathcal{E}=E$。
2. 在模体树$\mathcal{T}(G)$中，众多模体应该没有交集。也即 $M_i\cap M_j=\varnothing$。
3. 诱导出的模体应该捕获语义，例如，类似于化学领域中有意义的官能团。
4. 模体在数据集中的出现应该足够频繁，以便预训练的GNNs可以学习模体的语义信息，这些信息可以推广到下游任务。在分子断裂之后，分子数据集的基序词汇应该具有适度的大小。

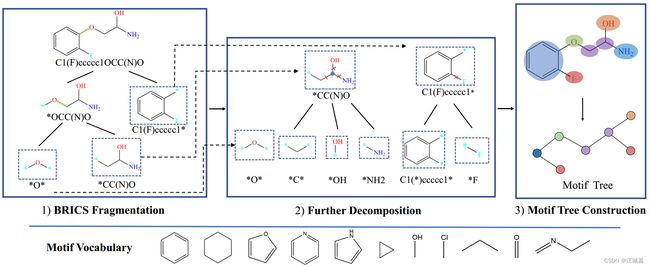
在图2中，我们展示了分子分割的框架。一般有三个程序，BRICS分割，进一步分解，模体树构建。可以通过在分子分割步骤之后预处理整个分子数据集来构建模体词汇表。

为了分割分子图和构建模体树，我们首先使用利用化学领域知识的反向合成感兴趣化学子结构(BRICS)算法[4]。BRICS定义了16条规则，打破了分子中与一系列化学反应相匹配的战略键。==“虚拟”==原子附着在切割位点的每一端，标志着两个片段可以连接在一起的位置。BRICS分割规则旨在保留具有有价值的结构和功能内容的分子成分，如芳香环。

然而，我们发现单独的BRICS不能产生分子图所需的模体。这是因为BRICS只基于有限的一组化学反应来断裂键，并且倾向于为一个分子生成几个大片段。此外，由于图结构的组合爆炸，我们发现BRICS产生了许多相同潜在结构的变体(例如，具有不同卤素原子组合的呋喃环)。模体词汇表很大(超过100k的独特片段)，而这些基序中的大多数在整个数据集中出现不到5次。

为了解决上述问题，我们在BRICS中引入了后处理过程。为了缓解组合爆炸，我们定义了两条作用于BRICS输出片段的规则：(1)断开一端原子在环中而另一端不在环中的键。(2)选择具有三个或三个以上相邻原子的非环原子作为新的模体，并断开相邻的键。第一个规则减少了环变体的数量，第二个规则断开了侧链。实验表明，这些规则有效地减少了模体词汇的规模，提高了模体的出现频率。

图2：分子断裂概述。一般来说，有三个步骤：1)首先基于BRICS分割分子图。2)进一步分解以减少模体的冗余。3)从分子图构建模体树。在对整个分子数据集进行预处理之后，构建了模体词汇表。

模体生成

在这里，我们提出了用于生成式自监督预训练的模体生成框架。模体生成任务的目标是让GNNs学习图模体的数据分布，以便预训练的GNNs可以通过对来自相似域的图形的几个微调步骤容易地推广到下游任务。

给定一个分子图$G=(V,E)$和一个GNN模型$f_{\theta }$，我们首先将分子图转换为模体树$\mathcal{T}(G)=(\mathcal{V},\mathcal{E},\mathcal{X})$。然后，我们可以通过GNN模型将该模体树上的似然性建模为$p(\mathcal{T}(G);\theta )$，它代表模体们是如何被标记和连接的。通常，我们的方法旨在通过最大化模体树的似然来预训练GNN模型$f_{\theta }$，即${\theta }^{\ast }={\text{argmax}}_{\theta }p(\mathcal{T}(G);\theta )$。为了建模模体树的似然，设计了拓扑和模体标签预测的特殊预测头（如下节所示）并与$f_{\theta }$一起优化。在预训练之后，只有GNN模型$f_{\theta }$被转移到下游任务。

我们注意到，大多数现有的图生成工作[17, 23]遵循自回归方式来分解概率目标，即$p(T(G);\theta )$。对于每个分子图，他们将其分解为一系列生成步骤。同样，在本文中，我们交错添加新的模体，并添加键将新添加的模体连接到现有的部分模体树。我们用置换向量$\pi$来确定模体的排序，其中$i^{\pi }$表示置换$\pi$中第$i$个位置的模体ID。因此，概率$p(T(G);\theta )$相当于所有可能排列的预期可能性，即，
$$p(T(G);\theta )={\mathbb{E}}_{\pi }[p_{\theta }({\mathcal{V}}^{\pi },{\mathcal{E}}^{\pi })],\text{\hspace{1em}(3)}$$
其中${\mathcal{V}}^{\pi }$表示置换的模体标签，${\mathcal{E}}^{\pi }$表示模体之间的边。

我们的形式允许各种顺序。为了简单起见，我们假设任何节点排序$\pi$具有相等的概率，并且在下面的部分中说明一个置换的生成过程时，我们也省略了下标$\pi$。给定排列顺序，生成模体树$\mathcal{T}(G)$的概率可以分解如下:
$$\log p_{\theta }(\mathcal{V},\mathcal{E})=\sum _{i=1}^{|\mathcal{V}|}\log p_{\theta }({\mathcal{V}}_i,{\mathcal{E}}_i|{\mathcal{V}}_{<i},{\mathcal{E}}_{<i}),\text{\hspace{1em}(4)}$$
在每个步骤$i$，我们使用在$i$之前生成的所有模体的模体属性${\mathcal{V}}_{<i}$和结构${\mathcal{E}}_{<i}$来生成新模体${\mathcal{V}}_i$和它的连边（蕴含于${\mathcal{E}}_i$）。

等式4描述了基元树的自回归生成过程。那么问题就是如何选择一个高效的生成序列，如何建模条件概率$\log p_{\theta }({\mathcal{V}}_i,{\mathcal{E}}_i|{\mathcal{V}}_{<i},{\mathcal{E}}_{<i})$。在下一节，我们介绍了两种高效的生成序列，BFS和DFS，并且展示了相应的自回归生成模型。

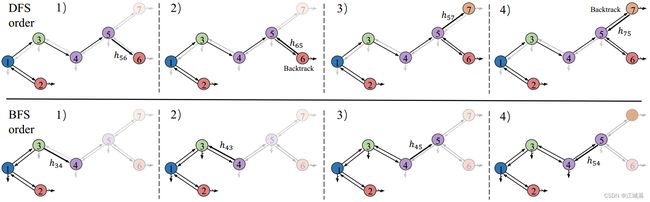
图3：模体生成顺序的图示。第一行是DFS订单的图示，第二行是BFS订单。

要从头开始生成模体树，我们需要首先选择模体树的根。在我们的实验中，我们简单地选择具有规范顺序中第一个原子的模体[34]。然后MGSSL在DFS或BFS顺序中生成图(见图3)。在DFS顺序中，对于每个被访问的模体，MGSSL首先进行拓扑预测：这个节点是否有要生成的子节点。如果生成了一个新的子模体节点，我们预测它的标签并迭代这个过程。当没有更多的孩子节点生成时，MGSSL进行回溯。至于BFS顺序，MGSSL逐层生成模体节点。对于第k层的模体节点，MGSSL进行拓扑预测和标签预测。如果生成了第k层中模体的所有子节点，MGSSL将移动到下一层。我们还注意到，BFS和DFS中的模体节点顺序不是唯一的，因为兄弟节点中的顺序是不明确的。在实验中，我们按照一个顺序进行预训练，并将这个问题和其他潜在的生成顺序留给未来的探索。

在每个时间步，模体节点从其他生成的模体接收信息以进行预测。当递增地构建模体树时，信息通过消息向量$h_{ij}$传播。形式上，假设${\hat{\mathcal{E}}}_t$是时间$t$的消息集。模型在时间$t$访问模体$i$，$x_i$表示模体$i$的嵌入，这可以通过池化模体$i$中的原子嵌入来获得。消息$h_{i,j}$通过先前的消息来更新：
$$h_{i,j}=\text{GRU}(x_i,\{h_{k,i}{\}}_{(k,i)\in {\hat{\mathcal{E}}}_t,k\ne j}),\text{\hspace{1em}(5)}$$
其中GRU负责模体树的消息传递：
$$s_{ij}=\sum _{(k,i)\in {\hat{\mathcal{E}}}_t,k\ne j}{\text{h}}_{k,i},\text{\hspace{1em}(6)}$$

$$z_{i,j}=\sigma ({\text{W}}^z{x}_i+{\text{U}}^z{s}_{i,j}+b^z),\text{\hspace{1em}(7)}$$

$$r_{k,i}=\sigma ({\text{W}}^r{x}_i+{\text{U}}^r{\text{h}}_{k,i}+b^r),\text{\hspace{1em}(8)}$$

$${\tilde{\text{h}}}_{i,j}=\tanh (\text{W}{x}_i+U\sum _{k=\mathcal{N}(i)\backslash j}{r}_{k,i}\odot {\text{h}}_{k,i}),\text{\hspace{1em}(9)}$$

$${\text{h}}_{i,j}=(1-z_{ij})\odot s_{ij}+z_{ij}\odot {\tilde{\text{h}}}_{i,j},\text{\hspace{1em}(10)}$$

拓扑预测：当MGSSL访问模体$i$时，需要对其是否有孩子要生成进行二元预测。我们通过一个隐藏层网络计算概率，该网络后接一个sigmoid函数，将信息和模体嵌入考虑在内:
p t = σ ( U d ⋅ τ ( W 1 d x i + W 2 d ∑ ( k , i ) ∈ E ^ t h k , i ) ) , (11) p_t=\sigma \left(U^d\cdot\tau(W^d_1x_i+W^d_2 \sum_{(k,i)\in \hat{\mathcal{E}}_t}h_{k,i}) \right), \tag{11} pt​=σ ​Ud⋅τ(W1d​xi​+W2d​(k,i)∈E^t​∑​hk,i​) ​,(11)
其中$d$是隐藏层的维度。

**模体标签预测：**当模体$i$生成子模体时，我们用以下公式预测子模体$j$的标签:
$$q_j=\text{softmax}(U^l\tau (W^l{h}_{ij})),\text{\hspace{1em}(12)}$$
其中$q_j$是在模体词汇$\mathcal{X}$上的分布，$l$是隐藏层维度。设${\hat{p}}_t\in \{0,1\}$和${\hat{q}}_j$是ground truth拓扑和模体标签值，模体生成损失是拓扑和基序标签预测的交叉熵损失之和:
$${\mathcal{L}}_{motif}=\sum _t{\mathcal{L}}_{topo}(p_t,{\hat{p}}_t)+\sum _j{\mathcal{L}}_{pred}(q_j,{\hat{q}}_j),\text{\hspace{1em}(13)}$$
在优化过程中，最小化上述损失函数对应于最大化等式4中的对数似然。请注意，在训练过程中，在每一步的拓扑和基序标签预测之后，我们用它们的ground truth来替换它们，以便MGSSL基于正确的历史进行预测。

多级自监督预训练

为了捕获分子中的多尺度信息，MGSSL被设计为一个分层框架，包括原子级和基序级任务(图1)。对于原子级预训练，我们利用属性屏蔽让GNNs首先学习节点/边属性的规律性。在属性屏蔽中，随机采样的节点和键属性(例如，原子数、键类型)被替换为特殊的屏蔽指示符。然后，我们应用GNNs来获得相应的节点/边嵌入(边嵌入可以作为边的端节点的节点嵌入的组合来获得)。最后，嵌入顶部的全连接层预测节点/边属性。交叉熵预测损失分别表示为${\mathcal{L}}_{atom}$和${\mathcal{L}}_{bond}$。

为了避免连续预训练中的灾难性遗忘，我们统一了多级任务，旨在最小化预训练中的混合损失:
$${\mathcal{L}}_{ssl}={\lambda }_1{\mathcal{L}}_{motif}+{\lambda }_2{\mathcal{L}}_{atom}+{\lambda }_3{\mathcal{L}}_{bond},\text{\hspace{1em}(14)}$$
其中${\lambda }_i$是损失的权重。然而，进行网格搜索以确定最佳权重是非常耗时的。这里，我们采用来自多任务学习的MGDA-UB算法[37]来有效地解决优化问题(等式14)。由于MGDA-UB通过弗兰克-沃尔夫算法[16]在每个训练步骤计算权重${\lambda }_i$，我们不必明确给出权重。训练过程的伪代码包含在附录中。

实验

数据集和数据划分

数据集和数据集分割。在本文中，我们主要关注分子性质预测任务，其中大规模的未标记分子是丰富的，而下游的标记数据是稀缺的。具体来说，我们使用从ZINC15数据库[38]中采样的250K未标记分子进行自监督的预训练任务。至于下游的微调任务，我们考虑MoleculeNet [45]中包含的8个二元分类基准数据集。附录中总结了详细的数据集统计数据。我们使用开源包RDKit[22]对来自不同数据集的SMILE字符串进行预处理。为了模拟真实世界的用例，我们通过scaffold-split [14，31]分割下游数据集，根据分子的结构分割分子。我们对随机数据分割进行了3次独立运行，并报告了平均值和标准偏差。

基线

我们针对GNNs的五种最先进的自监督预训练方法全面评估了MGSSL的性能：

• Deep Graph Infomax [41]最大化了整个图的表示与其采样子图的表示之间的互信息。

• Attribute masking [14]屏蔽节点/边特征，并让GNNs预测这些属性。

• GCC [30]将预训练任务设计为区分从某个节点采样的自网络和从其他节点采样的自网络。

• Grover [32]基于原子嵌入预测上下文属性，以将上下文信息编码到节点嵌入中。

• GPT-GNN [15]是一个生成性预训练任务，它预测被屏蔽的边和节点属性。