动态规划8：最长递增子序列问题（上）

本期题目

• 最长递增子序列
• 最大整除子集
• 最长递增子序列的个数

最长递增子序列

本期讨论的都一类问题，我们统称为最长递增子序列问题，这类问题都是由Leetcode第300题最长递增子序列问题衍生而来，我们先来讨论这道母题。

最长递增子序列：

题目描述： 给你一个整数数组nums，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

这个问题有一种最直观的做法，就是将$dp[i]$定义为以$nums[i]$开头的最长递增子序列。那么，如果$nums[i]$就是$nums[i:(n-1)]$的最大值，那么$dp[i]=1$；

否则，分别考察$dp[i+1],\cdots ,dp[n-1]$，$nums[i]<nums[j]$，接上以$nums[j]$开头的最长递增序列即可，于是，状态转移方程为$$dp[i]=\underset{j=i+1,\cdots ,n-1;nums[j]>nums[i]}{\max }dp[j]$$
再取$dp$数组的最大值即可，时间复杂度为$O(n^2)$，空间复杂度为$O(n)$，C++代码如下：

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        if(n==1) return 1;
        else{
            vector<int> dp(n,1);
            int maxLen =1;
            for(int i=n-2;i>=0;i--){
                for(int j=i+1;j<=n-1;j++){
                    if(nums[i]<nums[j]) dp[i]=max(dp[i],1+dp[j]);
                }
                maxLen=max(maxLen,dp[i]);
            }
            return maxLen;
        }
    }
};

复杂度分析： 时间复杂度$O(n^2)$，空间复杂度$O(n)$

Leetcode成绩： 执行用时：272 ms, 在所有 C++ 提交中击败了28.77% 的用户，内存消耗：10.3 MB, 在所有 C++ 提交中击败了36.96% 的用户

执行用时只击败了28.77%的人，说明时间复杂度还可以进一步优化，实际上，以上算法并不是最优的，还可以时间复杂度优化到$O(n\log n)$，只需要稍微更改一下$dp$数组的定义即可，为此，我们考察一下整个动态规划的过程即可。

例子： $nums=[10,9,2,5,3,7,101,18]$

实际上，求每一个$dp$值的时候，我们要的是把$nums[i]$接到它可以接到的最长的递增子序列上。

1. $i=7$时，只有一个递增子序列$[18]$
   
2. $i=6$时，$101$并不能接上这个递增子序列$[18]$，所以所以以之为头的最长递增子序列为$[101]$，此时有递增子序列$[18],[101]$
   
3. $i=5$时，$7$能接上这两个递增子序列，我们接上其中一个就好，如接上$[101]$，所以以$7$为头的最长递增子序列为$[7,101]$，此时长度为1的递增子序列有$[18],[101]$，长度为2的递增子序列有$[7,101]$
   
4. $i=4$时，$3$能接上的最长子序列就是那个长度为2的递增子序列，此时，长度为3的递增子序列有$[3,7,101]$，长度为2的递增子序列有$[7,101]$，长度为1的递增子序列有$[18],[101]$
   
5. $i=3$时，$5$不能接上长度为3的递增子序列，只能接上长度为2的递增子序列，此时长度为3的递增子序列有$[3,7,101],[5,7,101]$，长度为2的递增子序列有$[7,101]$，长度为1的递增子序列有$[18],[101]$
   
6. $i=2$时，$2$能接上长度为3的递增子序列，此时长度为4的递增子序列有$[2,5,7,101]$，长度为3的递增子序列有$[3,7,101],[5,7,101]$，长度为2的递增子序列有$[7,101]$，长度为1的递增子序列有$[18],[101]$
   
7. $i=1$时，$9$不能接上长度为4,3,2的递增子序列，只能接上长度为1的递增子序列，设接上$[101]$，此时长度为4的递增子序列有$[2,5,7,101]$，长度为3的递增子序列有$[3,7,101],[5,7,101]$，长度为2的递增子序列有$[7,101],[9,101]$，长度为1的递增子序列有$[18],[101]$
   
8. $i=0$时，$10$不能接上不能接上长度为4,3,2的递增子序列，只能接上长度为1的递增子序列，设接上$[101]$不能接上长度为4,3,2的递增子序列，只能接上长度为1的递增子序列，此时长度为4的递增子序列有$[2,5,7,101]$，长度为3的递增子序列有$[3,7,101],[5,7,101]$，长度为2的递增子序列有$[7,101],[9,101],[10,101]$，长度为1的递增子序列有$[18],[101]$
   

$nums[i]$能否接上某个递增子序列，只与$nums[i]$是否小于这个递增子序列的最小值，因此只与这个递增子序列的最小值有关，我们可以仅以这个递增子序列的最小值指代这个递增子序列，$dp[i]$储存长度为$i+1$的递增子序列的最小值。我们把上面几幅图的的序列全部换成其最小值，我们再来看这个新的$dp$在计算过程中的变化。

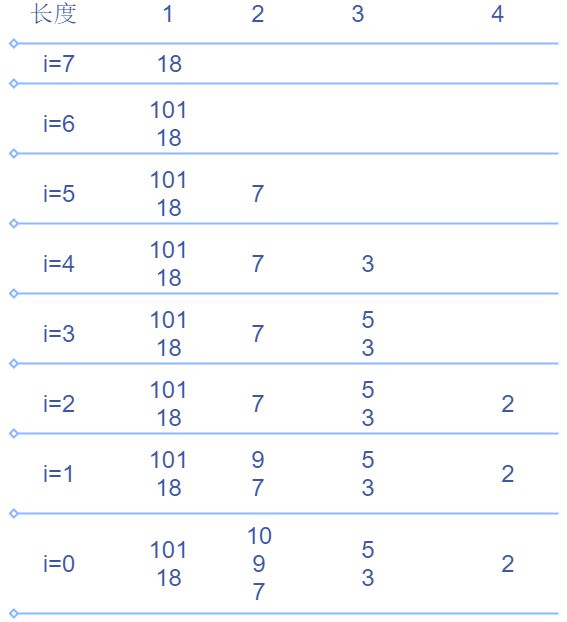
我们发现不论哪个阶段，所有递增子序列最小值的最大值构成一个严格单调减的序列。

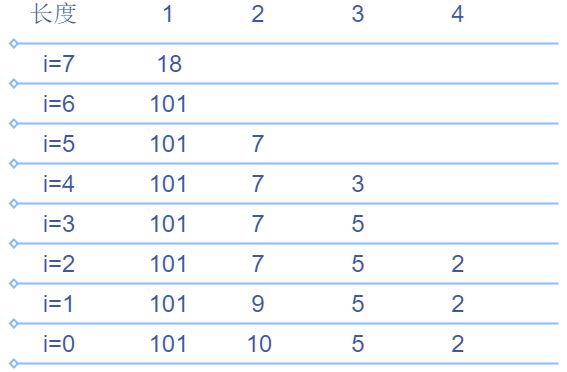
我们重新审视一下上面的计算过程：

1. $i=6$时，由于$101>dp[0]$，$101$不能接上所有长度为$1$的最长递增子序列，所以以$101$为头的只能说它自己，长度为1的递增子序列的最小值的最大值更新到$dp[0]=101$
2. $i=5$时，$7<dp[0]$，说明$7$至少能接上以$dp[0]=101$为头的长度为1的递增序列，成为长度为2的递增序列，因此长度为2的递增序列的头的最大值更新为$dp[1]=7$
3. $i=4$时，$3<dp[1]$，说明$3$至少能接上以$dp[1]=7$为头的长度为2的递增序列，成为长度为3的递增序列，因此长度为3的递增序列的头的最大值更新为$dp[2]=3$
4. $i=3$时，$dp[1]>5>dp[2]$，$5$至少能接上以$dp[1]=7$为头的长度为2的递增序列，成为长度为3的递增序列，但不能接上任意一条长度为3的递增序列，此时长度为3的递增序列的头的最大值更新为$dp[2]=5$
5. $i=2$时，$2<dp[2]$，说明$2$至少能接上以$dp[2]=5$为头的长度为3的递增序列，成为长度为4的递增序列，长度为4的递增序列的头的最大值更新为$dp[3]=2$
6. $i=1$时，$dp[0]>9>dp[1]$，$9$至少能接上以$dp[0]=101$为头的长度为1的递增序列，成为长度为2的递增序列，但不能接上任意一条长度为2的递增序列，此时长度为2的递增序列的头的最大值更新为$dp[1]=9$
7. $i=0$时，$dp[0]>10>dp[1]$，$10$至少能接上以$dp[0]=101$为头的长度为1的递增序列，成为长度为2的递增序列，但不能接上任意一条长度为2的递增序列，此时长度为2的递增序列的头的最大值更新为$dp[1]=10$
8. 最后再返回$dp$数组的长度即可

通过上面的计算过程我们就得到一种$O(n\log n)$的算法，我们作如下总结：

初始化： $dp[0]=nums[i],n=nums.size()$

for $i$ from $n-2$ to $0$:

1. 如果$nums[i]\ge dp[0]$，说明$nums[i]$不能接上任何一个递增子序列，只能独立成为一个长度为1的递增子序列，按照$dp[0]$的定义，更新$dp[0]=nums[i]$

2. 如果$nums[i]<dp[dp.size()-1]$，说明$nums[i]$至少能接上以$dp[dp.size()-1]$为头的长度为$dp.size()$的递增子序列，因此，$dp[dp.size()]=nums[i]$

3. 以上条件都不满足，则$dp[dp.size()-1]\le nums[i]<dp[0]$，dp数组是一个严格单调递减的序列，通过二分搜索，找出$j$满足$dp[j+1]\le nums[i]<dp[j]$，说明，$nums[i]$能接上以$dp[j]$为头的的长度为$j+1$的子序列，但不能接上任何一条长度为$j+2$的子序列，更新：$dp[j+1]=nums[i]$

返回：$dp$数组的长度

写成伪代码如下：

dp[0]=nums[i];
n=nums.size();
for(int i=n-2;i>=0;i--){
    if(nums[i]>=dp[0]) dp[0]=nums[i];
    else if(nums[i]

二分查找的复杂度为$\log [dp.size()]\le \log n$，所以时间复杂度不会超过$O(n\log n)$，空间复杂度为$O(dp.size())\le O(n)$，这比上面的动态规划算法快多了，我们称这种算法为动态规划+二分查找算法。

/*动态规划+二分查找算法*/
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        if(n==1) return 1;
        else{
            vector<int> dp;
            dp.push_back(nums[n-1]);
            for(int i=n-2;i>=0;i--){
                if(nums[i]<dp[dp.size()-1]) dp.push_back(nums[i]);
                else if(nums[i]>=dp[0]) dp[0]=nums[i];
                else{
                    //进行二分查找
                    int begin=0;
                    int end=dp.size()-1;
                    int mid=(begin+end)/2;
                    while(end-begin>=2){
                        if(dp[mid]==nums[i]){
                            end=mid;
                            break;
                        }else if(dp[mid]>nums[i]) begin=mid;
                        else end=mid;
                        mid=(begin+end)/2;
                    }
                    dp[end]=nums[i];
                }
            }
            return dp.size();
        }
    }
};

复杂度分析： 时间复杂度$O(n\log n)$，空间复杂度$O(n)$

Leetcode成绩： 执行用时：4 ms, 在所有 C++ 提交中击败了98.54% 的用户，内存消耗：10.1 MB, 在所有 C++ 提交中击败了94.32% 的用户

最大整除子集

实际上，只要定义了一个偏序关系，就能产生“最长递增子序列”问题。整除关系也是一种偏序关系，我们先给出问题描述。

最大整除子集

问题描述： 给你一个由无重复正整数组成的集合nums，请你找出并返回其中最大的整除子集answer，子集中每一元素对(answer[i], answer[j])都应当满足：

answer[i] % answer[j] == 0 ，或

answer[j] % answer[i] == 0

如果存在多个有效解子集，返回其中任何一个均可。

也就是要找一个最大子集，任意两个元素都满足其中一个能被另外一个整除。由于集合内元素的顺序无关紧要，我们将$nums$数组从小到大排列，如果我们已经得到一个整除子集$[a_0,a_1,\cdots ,a_{s-1}]$，并且$a_0\le a_1\le \cdots \le a_{s-1}\le a_s$，那么一定满足$a_{s-1}|a_{i}i=0,\cdots ,s-2$，$a|b$表示$a$能被$b$整除，整除关系是一个偏序关系，满足传递性，也就是：$$a|b,b|c\to a|c$$所以$a_s$能加入到整除子集$[a_0,a_1,\cdots ,a_{s-1}]$中当且仅当$a_s|a_{s-1}$。

很显然这就是一个LIS问题的变形，当然很容易想到$O(n^2)$的解法，即$dp$表示以$nums[i]$为最大元的最长整除子集，如果$nums[i]$不能整除任何$nums[j]0\le j<i$，那么$dp[i]$就是$nums[i]$，否则就接上能接上的最长的$dp[j]0\le j<i$。如果$dp[i]$接上$dp[j]j<i$，我们用一根指针从$dp[i]$指向$dp[j]$，如果不能接上任何元素，则指向空指针，于是我们有这种$O(n^2)$的解法

struct node{
    node* last;
    int depth;
    int val;
    node(int depth_,int val_,node* last_=nullptr){
        depth=depth_;
        val=val_;
        last=last_;
    }
    ~node(){}
};
class Solution{
    public:
    vector<int> largestDivisibleSubset(vector<int>& nums){
        int n=nums.size();
        if(n==1) return {nums[0]};
        else{
            sort(nums.begin(),nums.end());
            vector<node*> dp(n,nullptr);
            dp[0]=new node(1,nums[0]);
            int maxLen=1;
            node* res=dp[0];
            for(int i=1;i<n;i++){
                int l=0;
                node* dpj=nullptr;
                for(int j=0;j<i;j++){
                    if(nums[i]%nums[j]==0){
                        if(dp[j]->depth>l){
                            dpj=dp[j];
                            l=dp[j]->depth;
                        }
                    }
                }
                if(dpj==nullptr){
                    dp[i]=new node(1,nums[i]);
                }else{
                    dp[i]=new node(1+l,nums[i],dpj);
                }
                if(l+1>maxLen){
                    res=dp[i];
                    maxLen=l+1;
                } 
            }
            //回溯
            vector<int> r;
            while(res!=nullptr){
                r.push_back(res->val);
                res=res->last;
            }
            for(auto ptr:dp) delete ptr;
            return r;
        }
    }
};

复杂度分析：时间复杂度$O(n^2)$，空间复杂度为$O(n)$

Leetcode成绩： 执行用时：36 ms, 在所有 C++ 提交中击败了74.51% 的用户，内存消耗：9.5 MB, 在所有 C++ 提交中击败了14.46% 的用户

当然，我们也可以更改$dp$的定义，$dp[i]$存储所有长度为$i+1$的最大整除子集，这个问题我们当然没办法用二分查找去优化复杂度，但我们可以先从长的最大整除子集开始遍历，到小的最大整除子集，这样会比按顺序遍历会快一些。

struct Node{
    int val;
    Node* lastnode;
    Node(int val_,Node* lastnode_=nullptr){
        val=val_;
        lastnode=lastnode_;
    }
    ~Node(){}
};
class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        //先对nums进行排序
        sort(nums.begin(),nums.end());//时间复杂度O(nlg(n))
        int n=nums.size();
        vector<vector<Node*>> dp(n,vector<Node*>());
        int maxSize=1;
        dp[0]={new Node(nums[0])};
        for(int i=1;i<n;i++){
            bool f=false;
            for(auto t:dp[maxSize-1]){
                if(nums[i]%(t->val)==0){
                    Node* node = new Node(nums[i],t);
                    dp[maxSize].push_back(node);
                    maxSize++;
                    f=true;
                    break;
                }
            }
            if(f) continue;
            for(int j=maxSize-2;j>=0;j--){
                for(auto t:dp[j]){
                    if(nums[i]%(t->val)==0){
                        Node* node = new Node(nums[i],t);
                        dp[j+1].push_back(node);
                        f=true;
                        break;
                    }
                }
                if(f) break;
            }
            if(!f) dp[0].push_back(new Node(nums[i]));
        }
        Node* result_node = dp[maxSize-1][0];
        vector<int> result;
        while(result_node!=nullptr) {
            result.push_back(result_node->val);
            result_node=result_node->lastnode;
        }
        return result;
    }
};

复杂度分析：时间复杂度$O(n^2)$，空间复杂度为$O(n)$

Leetcode成绩： 执行用时：12 ms, 在所有 C++ 提交中击败了100% 的用户，内存消耗：10.1 MB, 在所有 C++ 提交中击败了11.77% 的用户

最长递增子序列的数目

现在我们来求最长递增子序列的数目，我们先来第一种解法：将$dp[i]$定义为以$dp[i]$为头的最长递增子序列的数目，将$dp2[i]$定义成以$dp[i]$为头的最长递增子序列的长度。$$\begin{array}{rl}& dp[i]=\{\begin{array}{ll}1& dp2[i]=1,i<n-1\\ {\sum }_{j>i,nums[j]>nums[i],dp2[j]=dp2[i]-1}dp[j]& dp2[i]>1,i<n-1\\ 1& i=n-1\end{array}\\ & maxLen=\underset{i=0,\cdots ,n-1}{\max }dp2[i]\\ & ans=\sum _{i=0,\cdots ,n-1;dp2[i]=maxLen}dp[i]\end{array}$$

按照这个状态转移方程，我们可以得到以下的解法：

/*解法1*/
class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        int n=nums.size();
        if(n==1) return 1;
        else{
            vector<int> dp(n,0);
            vector<int> dp2(n,0);
            dp[n-1]=1;
            dp2[n-1]=1;
            int ans=1;
            int maxLen=1;
            for(int i=n-2;i>=0;i--){
                for(int j=n-1;j>i;j--){
                    if(nums[i]<nums[j]){
                        if(dp2[j]>dp2[i]) {
                            dp[i]=dp[j];
                            dp2[i]=dp2[j];
                        }else if(dp2[j]==dp2[i]) dp[i]+=dp[j];
                    }
                }
                if(dp2[i]>0) dp2[i]++;
                else{
                    dp[i]=1;
                    dp2[i]=1;
                }
                if(dp2[i]>maxLen){
                    ans=dp[i];
                    maxLen=dp2[i];
                }else if(dp2[i]==maxLen) ans+=dp[i];
            }
            return ans;
        }
    }
};

复杂度分析：时间复杂度$O(n^2)$，空间复杂度$O(n)$

Leetcode成绩： 执行用时：116 ms, 在所有 C++ 提交中击败了76.72% 的用户，内存消耗：12.9 MB, 在所有 C++ 提交中击败了61.52% 的用户

现在我们来看第二种解法，我们还是以$nums=[10,9,2,5,3,7,101,18]$为例

1. $i=7$时，$nums[i]=18$，以$nums[i]$为头的最长递增序列只有一个，为$[18]$
   
2. $i=6$时，$nums[i]=101$，以$nums[i]$
   为头的最长递增序列只有一个，为$[101]$
   
3. $i=5$时，$nums[i]=7$，$nums[i]$可以接上所有长度为1的递增序列，全部都接上，得到
   
4. $i=4$时，$nums[i]=3$，$nums[i]$可以接上所有长度为2的递增序列，全部都接上
   
5. $i=3$时，$nums[i]=5$，$nums[i]$可以接上全部长度为2的递增序列，但不能接上全部长度为3的递增序列，于是得到
   
6. $i=2$时，$nums[i]=2$，$nums[i]$可以接上全部长度为3的递增序列，于是得到
   
7. $i=1$时，$nums[i]=9$，$nums[i]$只能接上全部长度为1的递增序列，于是得到
   
8. $i=0$时，$nums[i]=10$，$nums[i]$只能接上全部长度为1的递增序列，于是得到
   
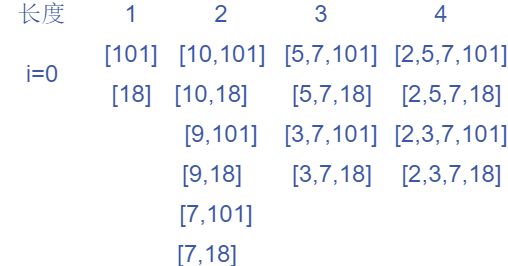
   所以得到的答案就是4，同样我们略去所有递增序列的后面的细节，只保留头部，得到
   
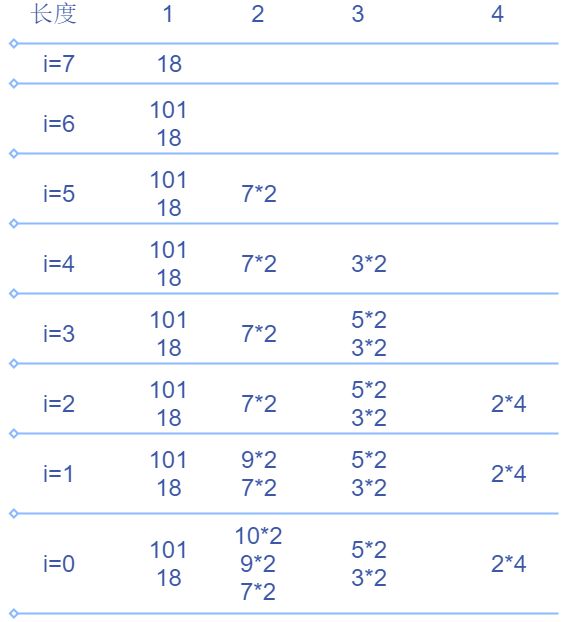
   这里计算过程和最长递增子序列是类似的，只不过在这里是能接上的最长递增子数组都接上，这里，我们的$dp$数组每一个单元都用一个链表储存，链表的每一个结点都是一个二元组，有一个元$val$，一个元$count$，$i=0$时的$dp$数组的结构如下：
   
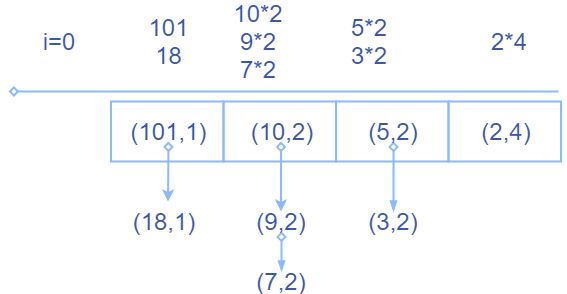
   现在我们假设在上面的例子的头部再插入一个$8$，那么，通过二分搜索$dp[1]<8<dp[3]$，所以8能接上长度为2的递增序列，不能接上长度为3的递增序列，那么能接上哪些递增序列的，很简单，能接上头部为10的两个递增序列和头部为9的两个递增序列。
   
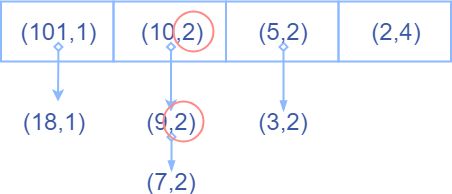
   这样再加上4个头部为8的长度为3的递增序列，于是dp数组变为
   
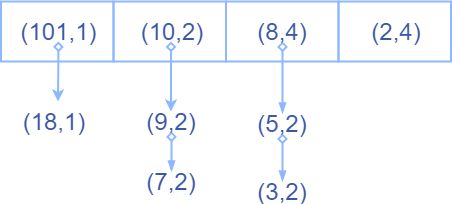
   重复上面的过程，最后把最后一个链表的所有结点的$count$加起来就是答案。

/*解法2*/
struct node{
    int val;
    int count;
    node* next;
    node(int val_,int nums_,node* next_=nullptr){
        val=val_;
        count=nums_;
        next=next_;
    }
};
class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        int n=nums.size();
        if(n==1) return 1;
        else{
            vector<node*> dp={new node(nums[n-1],1)};
            for(int i=n-2;i>=0;i--){
                if(nums[i]>dp[0]->val) dp[0]=new node(nums[i],1,dp[0]);
                else if(nums[i]==dp[0]->val) dp[0]->count++;
                else if(nums[i]<dp[dp.size()-1]->val){
                    node* newnode = new node(nums[i],0);
                    for(node* n=dp[dp.size()-1];n!=nullptr;n=n->next){
                        if(n->val>nums[i]) newnode->count+=n->count;
                        else break;
                    }
                    dp.push_back(newnode);
                }else{
                    //二分查找
                    int begin=0,end=dp.size()-1,mid=(begin+end)/2;
                    while(end-begin>=2){
                        if(dp[mid]->val==nums[i]){
                            end=mid;
                            begin=mid-1;
                        }else if(dp[mid]->val<nums[i]) end=mid;
                        else begin=mid;
                        mid=(begin+end)/2;
                    }
                    if(dp[end]->val==nums[i]){
                        for(node* n=dp[begin];n!=nullptr;n=n->next){
                            if(n->val>nums[i]) dp[end]->count+=n->count;
                            else break;
                        }
                    }else{
                        dp[end] = new node(nums[i],0,dp[end]);
                        for(node* n=dp[begin];n!=nullptr;n=n->next){
                            if(n->val>nums[i]) dp[end]->count+=n->count;
                            else break;
                        }
                    }
                }
            }
            int r=0;
            for(node* n=dp[dp.size()-1];n!=nullptr;n=n->next){
                r+=n->count;
            }
            for(auto t:dp) delete t;
            return r;
        }
    }
};