BF算法与KMP算法详解
目录
一、前言
二、BF算法
代码:
三、KMP算法
next数组:
关于为什么要找最长匹配前后缀:
代码:
KMP:
代码:
三、代码汇总:
一、前言
说到字符串匹配,就不得不提BF算法和KMP算法(当然,主要还是后者),虽然现在有的语言已经内置了字符串匹配函数,不过多数还是面向小规模的字符串(比如indexOf的暴力匹配),当面对大规模的字符串匹配时,还是要程序员自己设计算法。然而KMP算法这个东西说难不难,说简单也不能说简单,就挺容易忘的。。。所以我还是写个博客来记录一下。
二、BF算法
BF算法,即暴力(Brute Force)算法,设当前一个主字符串“ababcabccabcacbab",目标字符串为”abcac“,从主串中找到一个与目标字符串匹配的子串并返回下标。那么我们在主串上设置变量i记录主串位置,设置变量j记录目标字符串位置。
两者均从0下标开始遍历,当相等时记录i当前下标k(当后续匹配失败时,作为返回的标记),同时i与j均向后移动,重复该过程:
如果目标字符串遍历完毕,则说明已经找到子串,应当返回下标,即一开始的k位置,而由于i与j是同时移动的,所以两者移动距离相等,即 k = j - i。
如果在匹配的途中出现了不匹配的情况,那么两个字符串就必须同时回退,子串回退到0下标,而主串则回退到k + 1的位置(k位置是初始位置,已经匹配过了),即回退到 i - j + 1处。
代码:
//BF算法 str主串 sub目标串
public int BF(String str,String sub){
//strlen记录主串长度,sublen记录目标串长度
int strlen=str.length(),sublen=sub.length();
if(strlen==0||sublen==0)
return -1;
//主串与字串下标
int i=0,j=0;
while(i=sublen)
return i-j;
//未找到,返回-1
return -1;
} 三、KMP算法
KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) 。(我突然发现百科描述的比我好欸)
作为一种改良的算法,与BF算法最大的不同就在于他只需要回退目标串。而恰恰是这个目标串的回退是该算法的精髓,为此我们需要引出一个专门的next数组来作为我们回退的依据。
next数组:
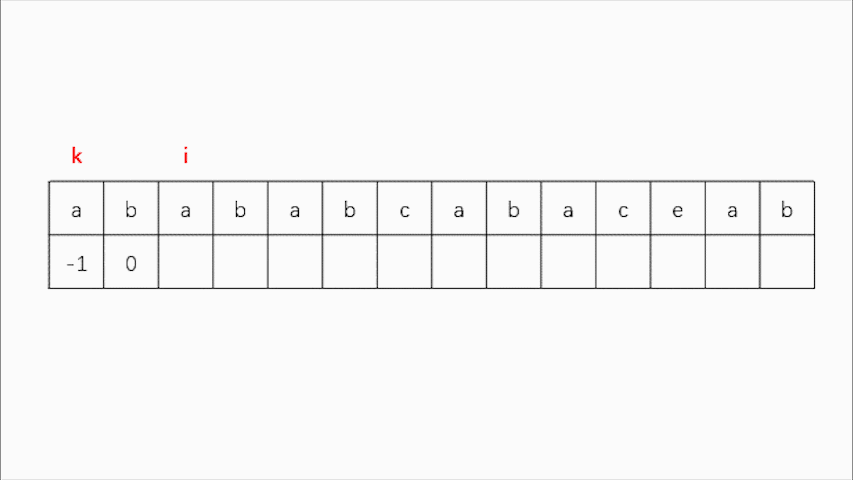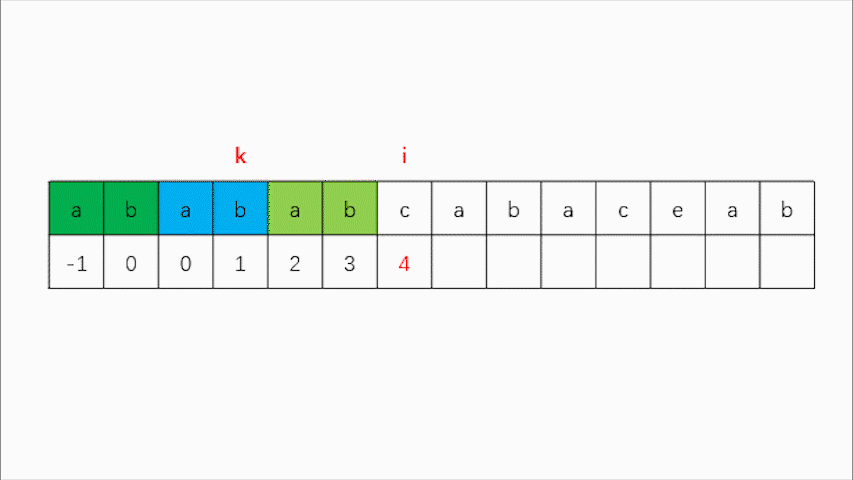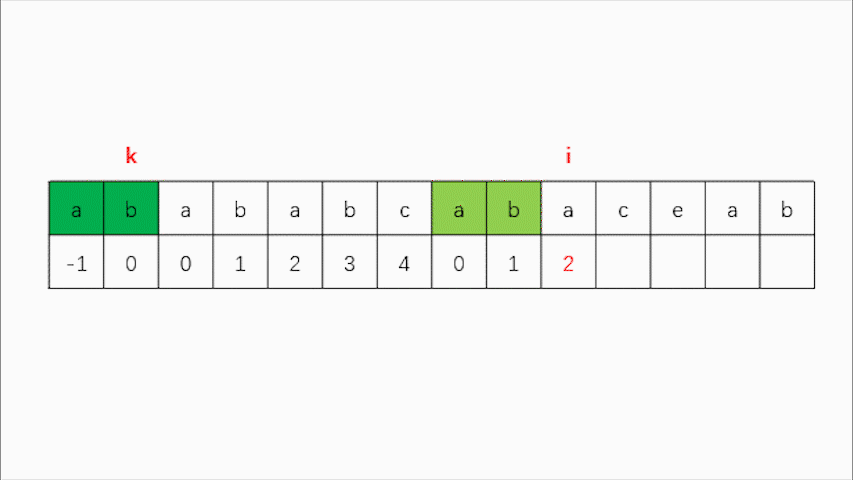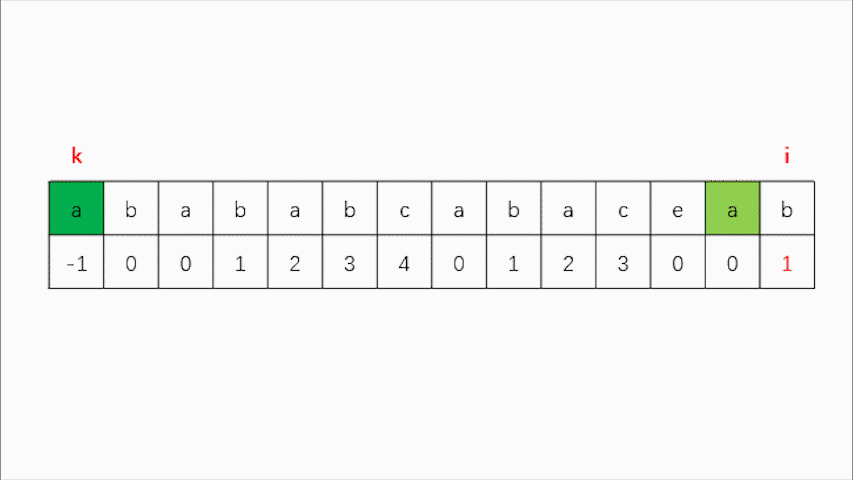
鉴于目标串过于简单,我们随便以一个字符串为例:”abababcabaceab“:
首先创建一个与目标字符串等长的数组,在0位置附上-1(为的是后续判断k是否回退到了0下标,且在0下标已经匹配过),在1位置附上0。设变量k=0,变量i=2。这样我们就做好了next数组的初始化操作。
随后开始寻找最长匹配前后缀,比如 "aba"的最长匹配前后缀就是"a",”abab“的最长匹配前后缀就是”ab“,”abcabca“的最长匹配前后缀长度就是0。
而对于我们这个数组而言,寻找最长匹配前后缀就是对比0到k的这段数组与i - k - 1到 i - 1的这段数组是否匹配,k与i同时从初始位置向后遍历,当0到i-1这段数组存在最长匹配前后缀时,便在i的位置填入该长度,而这段长度就等于k+1,当出现不匹配时,i不动,k回退到next[k]处,如果此时匹配则两者继续移动,如果仍不匹配,则k仍需回退,直到k的回退至0下标。
关于为什么要找最长匹配前后缀:
以这个情况为例,当此时的k需要回退时,k要回退到next[k]处,而很容易发现next[k]-1处与k-1处都是a。k在3位置的不匹配说明了k在2位置是匹配的,那么如果此时利用最长匹配前后缀回退到next[k]位置,则前面0到next[k]-1这段距离(即前缀)就不需要进行匹配验证,因为在k到达3位置时,后缀已经验证过了。
代码:
public static void getNext(int[] next,String sub){
int k=0,i=2;
next[0]=-1;
next[1]=0;
while (iKMP:
得到了next数组后,我们对于字符串的匹配就很容易了,我们同样使用BF算法中用的字符串:主字符串“ababcabccabcacbab",目标字符串”abcac“。
主串设变量i=0,目标串变量j=0,两者同时向后遍历,相等时i++,j++。一旦出现不同,则i不动,j回退到next[j]位置,其原因与我们求next数组中k回退的原因一致。
代码:
public void getNext(int[] next,String sub){//获取next数组
if(next.length==1){
next[0]=-1;
return;
}
next[0]=-1;
next[1]=0;
int i=2,k=0;
while (i=sub.length()){
return i-j;
}
return -1;
}
三、代码汇总:
public class Test {
//BF算法 str主串 sub目标串
public int BF(String str,String sub){
//strlen记录主串长度,sublen记录目标串长度
int strlen=str.length(),sublen=sub.length();
if(strlen==0||sublen==0)
return -1;
//主串与字串下标
int i=0,j=0;
while(i=sublen)
return i-j;
//未找到,返回-1
return -1;
}
public void getNext(int[] next,String sub){//获取next数组
if(next.length==1){
next[0]=-1;
return;
}
next[0]=-1;
next[1]=0;
int i=2,k=0;
while (i=sub.length()){
return i-j;
}
return -1;
}
public static void main(String[] args){
String str="ababcabccabcacbab";
String sub="abcac";
Test test=new Test();
System.out.println("BF算法: "+test.BF(str,sub));
System.out.println("KMP算法: "+test.KMP(str,sub));
}
}