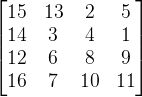LeetCode热题100 旋转图像
题目描述
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
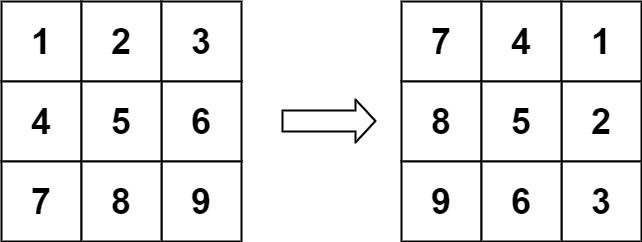
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
解题思路
可以摸索下有什么规律可寻,以示例二为例,枚举矩阵元素旋转90º后位置变化
第一行
5: (0,0) ——> (0,3)
1: (0,1) ——> (1,3)
9: (0,2) ——> (2,3)
11: (0,3) ——> (3,3)
第二行
2: (1,0) ——> (0,2)
4: (1,1) ——> (1,2)
······
由此可以总结出一个矩阵元素旋转后的位置变化公式:matrix[i][j] ——> matrix[j][n-1-i]
如果直接修改矩阵元素,前一个元素会覆盖掉它旋转后位置的元素,会造成数据丢失,如果将两个元素交换的话又会打乱矩阵,这样的话好像得借助一个辅助矩阵来临时储存元素,但是题目要求原地修改矩阵,不能借助另一个矩阵,啊,到底要怎么做,一定还有什么规律没有发现,盯着矩阵好好想想吧······
n坤时后——
山重水复疑无路,柳暗花明又一村。
我发现将每行元素反转后,每个元素以副对角线对称位置就是原位置旋转后的位置,
用公式表示:
matrix[i][j] 反转 ——> matrix[i][n-1-j]
(以副对角线翻转元素位置变化公式为: matrix[i][j]——>matrix[n-1-j][n-1-i] )
matrix[i][n-1-j] 以副对角线翻转 ——> matrix[n-1-(n-1-j)][n-1-i]=matrix[j][n-1-i]
由此可见,通过以上操作后就可以间接将矩阵中的每个元素移到旋转后的位置。
算法流程:
1.对矩阵每行反转
2.实现副对角线翻转操作,就是将矩阵副对角线两侧元素交换。
以下是算法Java实现:
class Solution {
public void rotate(int[][] matrix) {
int n=matrix.length;
// 反转
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
int temp = matrix[i][j];
matrix[i][j] = matrix[i][n - j - 1];
matrix[i][n- j - 1] = temp;
}
}
// 副对角线翻转
for(int i=0;i时间复杂度为O(n^2),空间复杂度为O(1)
其他方法
大自然的搬运工。
作者:
Krahets
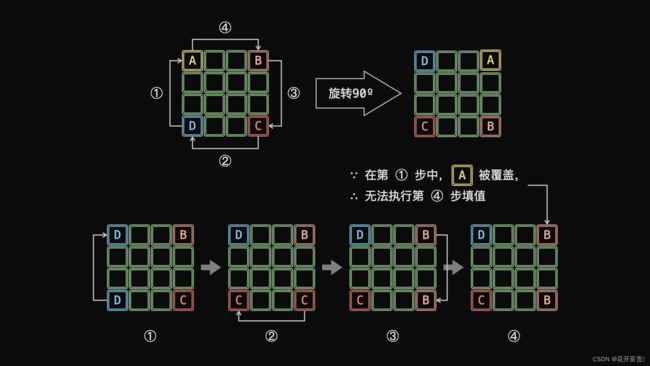
以位于矩阵四个角点的元素为例,设矩阵左上角元素 A 、右上角元素 B 、右下角元素 C 、左下角元素 D 。矩阵旋转 90º 后,相当于依次先后执行 D→A,C→D ,B→C,A→B 修改元素,即如下「首尾相接」的元素旋转操作:
A←D←C←B←A
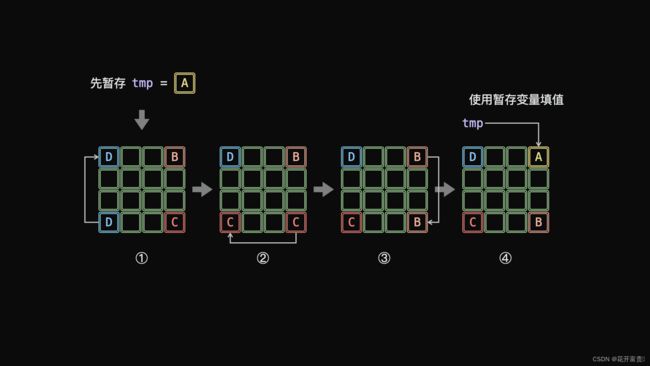
如上图所示,由于第 1 步 D→A 已经将 A 覆盖(导致 A 丢失),此丢失导致最后第 4 步 A→B 无法赋值。为解决此问题,考虑借助一个「辅助变量 tmp」预先存储 A ,此时的旋转操作变为:
暂存 tmp=A
A←D←C←B←tmp
如上图所示,一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 1/4的各元素为起始点执行以上旋转操作,即可完整实现矩阵旋转。
具体来看,当矩阵大小 n 为偶数时,取前 n/2行、前 n/2列的元素为起始点;当矩阵大小 n 为奇数时,取前 n/2行、前 (n+1)/2列的元素为起始点。
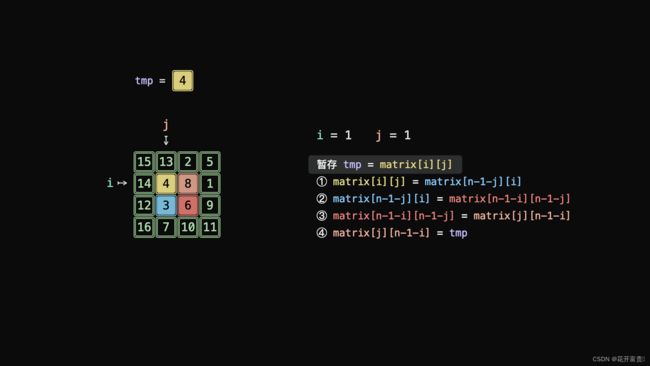
令 matrix[i][j]=A ,根据文章开头的元素旋转公式,可推导得适用于任意起始点的元素旋转操作:
暂存tmp=matrix[i][j]
matrix[i][j]←matrix[n−1−j][i]←matrix[n−1−i][n−1−j]←matrix[j][n−1−i]←tmp
算法执行流程:
算法Java实现:
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < (n + 1) / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
matrix[j][n - 1 - i] = tmp;
}
}
}
}
复杂度分析
时间复杂度O(N^2) : 其中 N 为输入矩阵的行(列)数。需要将矩阵中每个元素旋转到新的位置,即对矩阵所有元素操作一次,使用O(N^2) 时间。
空间复杂度 O(1) : 临时变量 tmp使用常数大小的额外空间。值得注意,当循环中进入下轮迭代,上轮迭代初始化的 tmp占用的内存就会被自动释放,因此无累计使用空间。
力扣官方题解