AVL树的 插入 和 删除

AVL树的 插入 和 删除

前面写的 二叉搜索树（BSTree）在文章的结尾提到了二叉搜索树的退化，也就是退化成了单支树，这样会使树的查找效率大大降到O(N)，这使得使用二叉搜索树变进行查找变的鸡肋，所以AVL树营运而生

AVL的定义

AVL树是由俄罗斯的两位数学家提出的解决搜索树的退化的的方法：向二叉搜索树中插入节点后，如果能够保证每个节点的左右子树高度之差的绝对值不超过1（通过一系列调整），即可降低树的高度，从而减少平均搜索长度
总结起来一颗具有以下性质的BSTree就是AVL树：

1. 他的左右子树的高度差的绝对值不超过1（也就是1、0、-1）
2. 他的左右子树都是AVL树

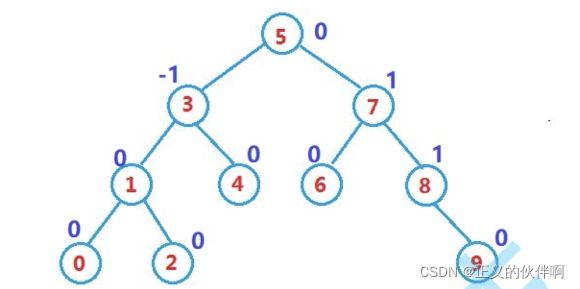
搜索二叉树的高度就会很平均。如果他有N个节点，其高度可保持在O(log2N)，搜索的时间复杂度可以保持在O(log2N)

AVL树节点的创建

建立二叉树之前要考虑的就是 节点结构的选择，我们选择的是三叉链：

	template<class T>
	struct AVLTreeNode
	{
		AVLTreeNode(const T x = T())
			:left(nullptr)
			, right(nullptr)
			, parent(nullptr)
			, bf(0)
			,val(x)
		{}

		AVLTreeNode* left;
		AVLTreeNode* right;
		AVLTreeNode* parent;  //多出一个指向父节点
		T val;
		int bf;              //这是平衡因子对后面的旋转至关重要
	}; 

平衡因子bf
你会注意到在整个结构中多出了一个bf平衡因子，这个值每个节点都含有，对后面节点的插入、删除之后调整数的高度起着至关重要的作用。
他的值等于：右子树的高度 - 左子树的高度
根据AVL树的定义，每个节点的bf值理论上只可能有三种情况：1，0，-1。所以当bf出现其他值的时候就代表树不平衡了，需要调整了

AVL的插入

在节点插入之前要搞明白几点：

• 插入的节点的bf为0，因为其左右子树均为空！！！
• 插入节点不影响该节点的bf的值，而可能会影响插入节点以上的节点，这种影响自下向上传递，具体表现在自下而上影响的路径上所有的节点的bf都要修改，所以我们要从插入节点向上检查这条路径上的每个节点的bf的值
• 当自下向上传递的过程中，如果有的节点的bf出现除了（1,0，-1）以外的值，就要停下来进行调整，随后继续向上检查，具体怎么调整插入后的不平衡下面会介绍四种旋转方式

AVL树插入的思路很简单就两步

1. 插入（这部分与BSTree相同）
2. 调整

调整

调整的过程是从插入的节点开始向上遍历，直到根节点

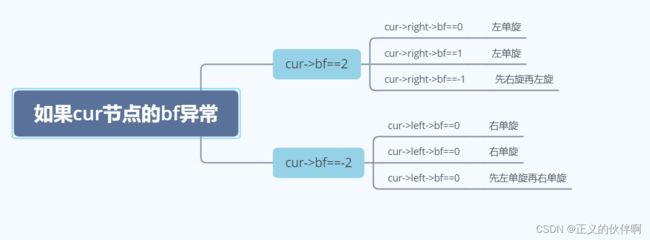
• 如果bf的值不合法，就对其进行旋转
• 如果bf的值合法，继续向上遍历（如果bf== 0，就不用继续向上了，从该节点向上的所有节点不会受到插入的影响，所以只有当bf == 1或bf ==-1的时候才需要继续向上）

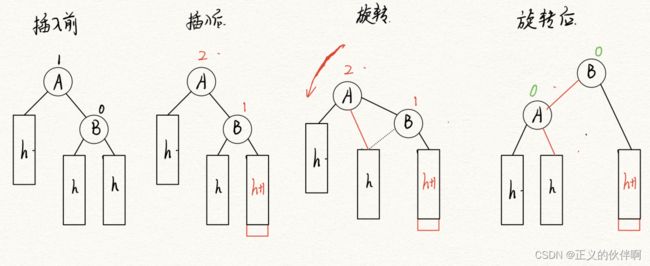
插入的左旋

左旋我们发现是当我们检查到A节点的bf值为2时代表右子树比左子树高2，其次B节点的值为1（重点在于1代表的也是右高左低），**所以总结一下左旋的特点就是：右高左低bf为2，找其右子树依然右高左低（bf为1）**这是左旋必须满足的条件！

注意
但是实际上广义上的左旋是不止B这个节点的bf的值为1可左旋，为0也可以左旋（但是在插入节点的情况下是不可能发生的（自己可以想一想）！！，但是这种情况在删除的时候就会出现！）

代码
注意这里的father节点代表的是A节点

		void left_rotate(Node* father)
		{
			Node* subR = father->right;
			Node* subRL = subR->left;

			subR->left = father;
			father->right = subRL;


			//处理subLR的parent的指向
			if(subRL!=NULL)
			subRL->parent = father;
			//处理subL的parent的指向
			if (father->parent == nullptr)  //如果father是根节点要特别注意
			{
				root=subR;
				subR->parent = nullptr;

			}
			else   //father不是根节点
			{
				Node* grandfather = father->parent;
				if (grandfather->left == father)
					grandfather->left = subR;
				else
					grandfather->right = subR;

				subR->parent = grandfather;
			}

			//处理father节点parent的指向
			father->parent = subR;

			father->bf = 0;
			subR->bf = 0;
		}

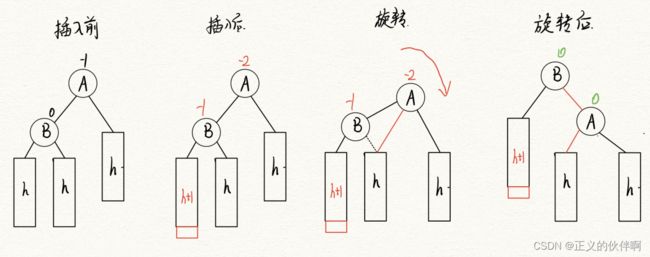
插入右旋

右旋我们发现是当我们检查到A节点的bf值为-2时代表左子树比右子树高2，其次B节点的值为-1（重点在于-1代表的也是左高右低），**所以总结一下左旋的特点就是：左高右低bf为2，找其左子树依然左高右低（bf为1）**这是右旋必须满足的条件！

注意
但是实际上广义上的右旋是不止B这个节点的bf的值为1可右旋，为0也可以右旋（但是在插入节点的情况下是不可能发生的（自己可以想一想）！！，但是这种情况在删除的时候就会出现！）

代码
注意这里的father节点代表的是A节点

void right_rotate(Node* father)
		{
			Node* subL = father->left;
			Node* subLR = subL->right;

			subL->right = father;
			father->left = subLR;


			//处理subLR的parent指向
			if(subLR!=nullptr)
			subLR->parent = father;
			//处理subL的parent的指向
			if (father->parent == nullptr)  //如果father是根节点要特别注意
			{
				root=subL;
				subL->parent = nullptr;

			}
			else   //father不是根节点
			{
				Node* grandfather = father->parent;
				if (grandfather->left == father)
					grandfather->left = subL;
				else
					grandfather->right = subL;

				subL->parent = grandfather;
			}

			//处理father节点parent的指向
			father->parent = subL;

			father->bf = 0;
			subL->bf = 0;
		}

左右旋

上面的情况都是一边高，要么都是左边高，要么都是右边高，下面的就和上面的不同

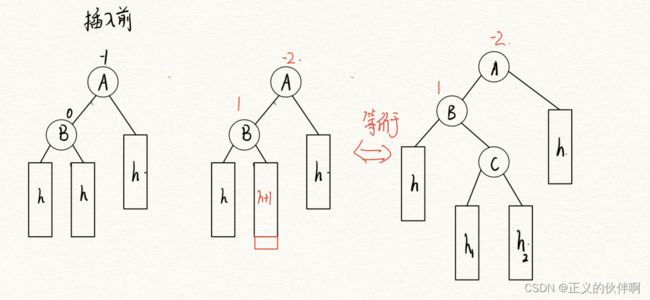
• 首先分析一下在哪插入

A节点是左边高，我们就插入B节点的右子树，使B节点右边高。注意 等价于后的C节点以及其子树（从h+1方框变化来，这样写是为了下面部分旋转看着方便），其总高度为h+1，如果h==0那么插入的节点就是C节点，由于C树的总高度为h+1则C节点的左右子树的高度满足Max(h1,h2)==h 并且|h1-h2|==1(avl树的定义)，这里要多加注意！！！，不要认为h1和h2相等，这里会影响旋转后的bf因子调整

• 接下来是局部左单旋 和 整体右单旋
  

调整完之后我们就明白了为什么要先左单旋：旋转完之后都是左边高了（满足右单旋的旋转条件了！！！）
所以接下来自然就是右单旋

• 最终结果：
  

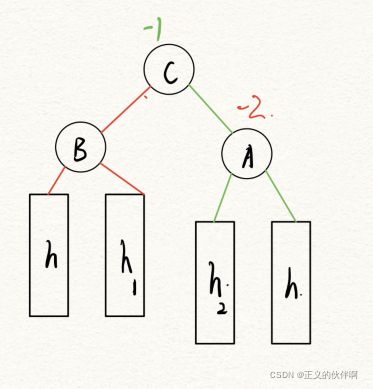
调整旋转之后的节点的平衡因子

我们发现左单旋和右单旋，旋转完之后所有节点的bf就都为0了，但是左右单旋并不是这样（如上图），很明显A的平衡因子不等于-2，所以这里就要修改旋转后的节点bf值，由于h1和h2的高度不确定，所以要分类讨论：

上面已经对C树进行分析（如下）

注意 等价于后的C节点以及其子树（从h+1方框变化来，这样写是为了下面部分旋转看着方便），其总高度为h+1，如果h==0那么插入的节点就是C节点，由于C树的总高度为h+1则C节点的左右子树的高度满足Max(h1,h2)==h 并且|h1-h2|==1(avl树的定义)，这里要多加注意！！！，不要认为h1和h2相等，这里会影响旋转后的bf因子调整

我们发现C节点的bf是影响h1和h2 的决定性因素

• 如果C节点的bf == 1，那么可以推出h2 高度为h，h1的高度为h-1
• 如果C节点的bf == -1，那么可以推出h2 高度为h-1，h1的高度为h
• 如果C节点的bf == 0，那么可以推出h2 高度为h，h1的高度为h

接下来我们只需要根据上面的情况进行分类讨论，并对照结果图将相应节点的bf值修改即可

右左旋

和左右单旋同理，这里就不演示了

AVL的删除

删除的主体思路和BSTree一样，这个方法具体在这片博客->BSTree，下面就如何删除节点分情况讨论一下：这里cur是要删除的节点，father是其父节点

• 1.删除的节点为叶子节点，直接删除，修改父节点的bf并从该节点的父节点向上调整，这个很好理解不用多说。
  

下面两种情况由于删除之前就是AVL树，又因为有一个子树为空，所以另一个子树（非空）一定只包含一个节点！，搞清楚这点很重要，这种节点一定是叶子节点的上一层！！！！ 这里虽然是删除该节点实际上等价于删除的是他的唯一一个非空节点

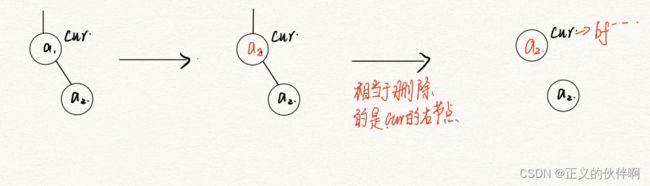
• 2.删除的节点左子树为空，右子树非空： 相当于删除右子树，修改该节点的bf并向上调整
  具体操作就是将非空节点的值赋给cur，这时删除cur就是等价删除cur的非空节点，最后从cur开始向上调整平衡因子
  

• 3.删除的节点右子树为空，左子树非空： 相当于删除左子树，修改该节点的bf并向上调整
  具体操作就是将非空节点的值赋给cur，这时删除cur就是等价删除cur的非空节点，最后从cur开始向上调整平衡因子
  

• 4.左右子树都不为空，用替换删除法，找左子树的最大节点（最右边节点，这个节点右子树一定为空）实际上就转化成了上面三种情况

删除的主体思路有了之后，接下来是如何对删除后的树进行调整，删除的调整和插入本质上相同，细节上略有不同：

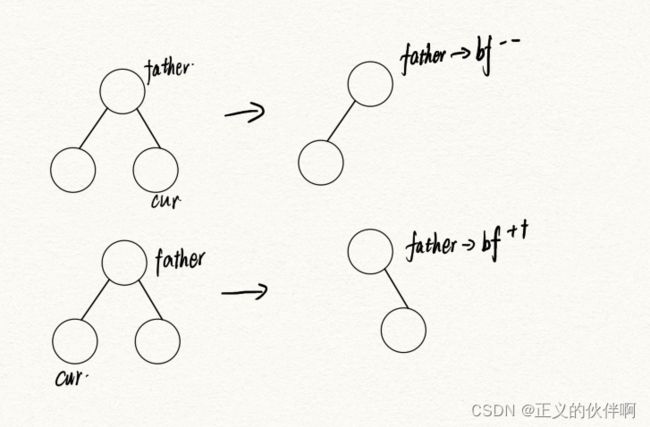
bf调整原则：

• 1. 删左节点，父节点的bf++
• 2. 删右节点，父节点的bf–
• 3. bf为0继续向上调整，bf为1或-1停止向上调整（与插入正好反过来）
• 4. cur->bf为2的时候情况就与插入不同了，插入的时候调整的是插入的节点所在的半边子树，而删除要调整的是删除节点对面那一半进行旋转（这点很重要！！！），也就是如果cur节点的bf为2，意味着右边高删除的节点一定在cur的左子树，接下来要调整右子树

旋转调整
与插入不同的是：删除左右单旋各自会出现一种新的情况，这种情况是插入中不可能发生的：

由于插入的时候一定是插入的那半边子树高，所以插入的时候只能在B的左右一个子树插入，所以B树的平衡因子不可能为0，而删除就不同了删除节点影响的是另一半边子树，旋转的也是另一半边子树（上面删除的地方一定是是高度为h的那颗子树），所以这种情况就出现了，这种情况依然是按照左单旋和右单旋处理。旋转完成之后记得要调整整个树的bf值

删除其他的旋转和旋转后旋转因子的设置均与插入相同。

整个一个AVL树的插入和删除以及层序遍历的代码如下：

#include
#include
#include
namespace sht
{
	template<class T>
	struct AVLTreeNode
	{
		AVLTreeNode(const T x = T())
			:left(nullptr)
			, right(nullptr)
			, parent(nullptr)
			, bf(0)
			,val(x)
		{}

		AVLTreeNode* left;
		AVLTreeNode* right;
		AVLTreeNode* parent;
		T val;
		int bf;
	};

	template<class T>
	struct AVL
	{
		typedef AVLTreeNode<T> Node;
		AVL()
			:root(nullptr)
		{

		}

		int height(Node *root)
		{
			if (root == nullptr)
				return 0;
			return max(height(root->left), height(root->right)) + 1;
		}

		bool _Isbalance(Node* root)
		{
			if (root == nullptr)
				return true;

			int bf = height(root->right) - height(root->left);
			if (bf > 1 || bf < -1)
				return false;

			return _Isbalance(root->left) && _Isbalance(root->right);

		}

		void Isbalance()
		{
			int ret = _Isbalance(root);
			cout << endl;
			if (ret == 1)
				cout << "Tree is balance" << endl;
			else
				cout << "Tree is not balance" << endl;
		}



		bool Insert(const T& data)
		{
			//插入过程
			Node* cur = root;
			Node* father = root;
			if (root == nullptr)
			{
				root = new Node(data);
				cur = root;
			}
			else
			{
				while (cur)
				{
					if (data > cur->val)
					{
						father = cur;
						cur = cur->right;
					}
					else if (data < cur->val)
					{
						father = cur;
						cur = cur->left;
					}
					else
						return false;
				}

				cur = new Node(data);
				if (data > father->val)
					father->right = cur;
				else
					father->left = cur;

				cur->parent = father;
			}

			//旋转过程
			while (father)
			{
				//1. 更新插入节点附近节点的平衡因子bf，注意：一个节点的bf值由该节点的左右子树决定 
				if (father->left == cur)
				{
					(father->bf)--;
				}
				else if (father->right == cur)
				{
					(father->bf)++;
				}

				//2. 检查平衡因子bf，判断是否需要旋转
				if (father->bf == 0)  //当bf为0时，插入新节点对bf的影响从这个节点开始就不会向上传递了，所以就不需要继续检查下去了
					break;
				else if (father->bf == 2 || father->bf == -2)  //当bf为2时就不满足AVL树的定义，需要旋转处理成AVL
				{
					//需要旋转
					if (father->bf == -2 && father->left->bf == -1) //左单旋
					{
						right_rotate(father);
					}
					else if (father->bf == 2 && father->right->bf == 1)
					{
						left_rotate(father);
					}
					else if (father->bf == 2 && father->right->bf == -1 ) //  从上往下一次是： 节点father的右子树高   father->right的左子树高 
					{
						Node* subR = father->right;
						Node* subRL = subR->left;
						int bf = father->right->left->bf;

						right_rotate(father->right);  //先右旋，使节点father和father->right的右子树 都 比左子树高
						left_rotate(father);          // 再左旋就平衡了

						if (bf == 1)         //插入的节点在subRL的右子树
						{
							subR->bf = 0;
							father->bf = -1;
						}
						else if (bf == -1)   //插入的节点在subRL的左子树
						{
							subR->bf = 1;
							father->bf = 0;
						}
						else if (bf == 0)   //此为特殊情况：即插入的节点正好是subRL节点 （这个情况就三个节点）
						{
							subR->bf = 0;
							father->bf = 0;
						}
					}
					else if (father->bf == -2 && father->left->bf == 1 /*&& father->left->right->bf == -1*/)
					{
						Node* subL = father->left;
						Node* subLR = subL->right;
						int bf = father->left->right->bf;

						left_rotate(father->left);
						right_rotate(father);
						
						if (bf == 1)         //插入的节点在subRL的右子树
						{
							subL->bf = -1;
							father->bf = 0;
						}
						else if (bf == -1)   //插入的节点在subRL的左子树
						{
							subL->bf = 0;
							father->bf = 1;
						}
						else if (bf == 0)   //此为特殊情况：即插入的节点正好是subRL节点 z
						{
							subL->bf = 0;
							father->bf = 0;
						}

					}

				}
				else
				{
					father = father->parent;
					cur = cur->parent;
				}

			}



			return true;
		}


		//删除的情况：
		// 1.删除的节点为叶子节点，直接删除，修改父节点的bf并从该节点的父节点向上调整
		//  下面两种情况由于删除之前就是AVL树，又因为有一个子树为空，所以另一个子树（非空）一定只包含一个节点！，搞清楚这点很重要，这种节点一定是叶子节点的上一层！！！！
		//  这里虽然是删除该节点实际上删除的是他的唯一一个非空节点
		// 2.删除的节点左子树为空，右子树非空： 相当于删除左子树，修改该节点的bf并向上调整
		// 3.删除的节点右子树为空，左子树非空： 相当于删除右子树，修改该节点的bf并向上调整
		//
		// 4.左右子树都不为空，用替换删除法，找右子树的最小节点（最左边节点，这个节点左子树一定为空）实际上就转化成了上面三种情况




		// bf调整原则：
		// 1. 删左节点，父节点的bf++
		// 2. 删右节点，父节点的bf--
		// 3. bf为0继续向上调整，bf为1或-1停止向上调整
		// 4. cur->bf为2的时候情况就与插入不同了，插入的时候调整的是插入的节点所在cur的半边子树，而删除要调整的是删除节点对面那一半进行旋转（这点很重要！！！，我在这上面卡了半天）
		//   旋转的操作与插入相同
		bool erase(const T& x)
		{
			if (root == nullptr)   //开头检查一下是否是空树
				assert(root == nullptr);
			Node* cur = root;
			Node* father = root;

			while (cur)
			{
				if (cur->val < x)
				{
					father = cur;
					cur = cur->right;
				}
				else if (cur->val > x)
				{
					father = cur;
					cur = cur->left;
				}
				else   
				{
					//删除操作
					if (cur->left == nullptr || cur->right == nullptr) //左右子树至少一个为空
					{
						if (cur == root)   //cur是根结点的情况要考虑一下！
						{
							root = (cur->left == nullptr) ? cur->right : cur->left;  //不可能出现旋转的情况
						}
						else if (cur->left == nullptr && cur->right == nullptr )  //左右子树均为空
						{
							if (father->left == cur)
							{
								father->left = nullptr;
								delete cur;
								father->bf++;
							}
							else
							{
								father->right = nullptr;
								delete cur;
								father->bf--;
							}

							Erase_rotate(father);
						}
						else  if(cur->left==nullptr && cur->right != nullptr)  //左空右不空
						{
							cur->val = cur->right->val;
							Node* temp = cur->right;
							cur->right = nullptr;
							delete temp;

							cur->bf--;
							Erase_rotate(cur);
						}
						else if (cur->right == nullptr && cur->left == nullptr)  //右空左不空
						{
							cur->val = cur->left->val;
							Node* temp = cur->left;
							cur->left = nullptr;
							delete temp;

							cur->bf++;
							Erase_rotate(cur);
						}

					}
					else  //左右子树都不为空 
					{
						//找到右子树中的最小值与cur节点的值进行替换

						//找右子树最小节点,也就是右子树的最左边的节点，这个节点：左子树一定为null，右子树未知
						Node* Newcur = cur->left;
						Node* Newcur_father = cur;
						while (Newcur->right)
						{
							Newcur_father = Newcur;
							Newcur = Newcur->right;
						}

						cur->val = Newcur->val;

						//现在要搞清楚等效删除的是哪个节点，以及从哪个节点开始向上检查！
						if (Newcur_father == cur)
						{
							if (Newcur->left) //相当于删除的是Newcur的右节点，改变Newcur的bf，并从Newcur节点向上检查
							{
								Newcur->val = Newcur->left->val;

								Node* temp = Newcur->left;
								Newcur->left = nullptr;
								delete temp;

								Newcur->bf++;
								Erase_rotate(Newcur);
							}
							else         //相当于删除的是Newcur节点，改变Newcur_father的bf，并从Newcur_father向上检查
							{
								Newcur_father->left = nullptr;
								delete Newcur;

								Newcur_father->bf++;  //这是if (Newcur_father == cur)两种情况的本质区别
								Erase_rotate(Newcur_father);
							}
						}
						else
						{
							if (Newcur->left) //相当于删除的是Newcur的右节点，改变Newcur的bf，并从Newcur节点向上检查
							{
								//这种情况就是上面  左子树为空右子树不为空

								Newcur->val = Newcur->left->val;

								Node* temp = Newcur->left;
								Newcur->left = nullptr;
								delete temp;

								Newcur->bf++;
								Erase_rotate(Newcur);
							}
							else         //相当于删除的是Newcur节点，改变Newcur_father的bf，并从Newcur_father向上检查
							{
								//这种情况就是上面  左右子树 均为空的删除情况

								Newcur_father->right = nullptr;
								delete Newcur;

								Newcur_father->bf--;
								Erase_rotate(Newcur_father);
							}
						}
					}
					return true;
				}
			}

			return false;
		}


		void print()  //层序遍历
		{
			queue<Node*> q;
			q.push(root);
			while (!q.empty())
			{
				if (q.front() != NULL)
				{
					q.push(q.front()->left);
					q.push(q.front()->right);
				}

				Node* tmp = q.front();
				q.pop();

				if (tmp == nullptr)
					printf("null ");
				else
					printf("%d ", tmp->val);
			}
		}
	private:
		Node* root;
		void right_rotate(Node* father)
		{
			Node* subL = father->left;
			Node* subLR = subL->right;

			subL->right = father;
			father->left = subLR;


			//处理subLR的parent指向
			if(subLR!=nullptr)
			subLR->parent = father;
			//处理subL的parent的指向
			if (father->parent == nullptr)  //如果father是根节点要特别注意
			{
				root=subL;
				subL->parent = nullptr;

			}
			else   //father不是根节点
			{
				Node* grandfather = father->parent;
				if (grandfather->left == father)
					grandfather->left = subL;
				else
					grandfather->right = subL;

				subL->parent = grandfather;
			}

			//处理father节点parent的指向
			father->parent = subL;

			father->bf = 0;
			subL->bf = 0;
		}


		void left_rotate(Node* father)
		{
			Node* subR = father->right;
			Node* subRL = subR->left;

			subR->left = father;
			father->right = subRL;


			//处理subLR的parent的指向
			if(subRL!=NULL)
			subRL->parent = father;
			//处理subL的parent的指向
			if (father->parent == nullptr)  //如果father是根节点要特别注意
			{
				root=subR;
				subR->parent = nullptr;

			}
			else   //father不是根节点
			{
				Node* grandfather = father->parent;
				if (grandfather->left == father)
					grandfather->left = subR;
				else
					grandfather->right = subR;

				subR->parent = grandfather;
			}

			//处理father节点parent的指向
			father->parent = subR;

			father->bf = 0;
			subR->bf = 0;
		}



		// bf调整原则：
		// 1. 删左节点，父节点的bf++
		// 2. 删右节点，父节点的bf--
		// 3. bf为0继续向上调整，bf为1或-1停止向上调整
		// 4. cur->bf为2的时候情况就与插入不同了，插入的时候调整的是插入的节点所在cur的半边子树，而删除要调整的是删除节点对面那一半进行旋转（这点很重要！！！，我在这上面卡了半天）
		//   旋转的操作与插入相同
		void Erase_rotate(Node* cur)  //删除节点的操作函数 传入的是已经修改过bf的删除节点的父节点
		{
			Node* prev = nullptr;
			while (cur)
			{

				if (cur->bf == 1 || cur->bf == -1)
					break;
				else if (cur->bf == 0)
				{
					prev = cur;
					cur = cur->parent;
				}
				else if (cur->bf == 2)
				{
					if (cur->right->bf == 1)  //左单旋
					{
						left_rotate(cur);
						prev = cur->parent;
						cur = prev->parent;

						continue;
					}
					else if (cur->right->bf == -1)  //先来一个右单旋 再来一个左单旋
					{
						Node* subR = cur->left;
						Node* subRL = subR->left;
						int _bf = subRL->bf;
						right_rotate(cur->right);
						left_rotate(cur);

						if (_bf == 1)
						{
							cur->bf = -1;
							subR->bf = 0;
						}
						else if (_bf == -1)
						{
							cur->bf = 0;
							subR->bf = 1;
						}
						else if (_bf == 0)
						{
							cur->bf = 0;
							subR->bf = 0;
						}

						cur = subRL->parent;
						prev = subRL;
						continue;
					}
					else if (cur->right->bf == 0)
					{
						left_rotate(cur);
						cur->parent->bf = -1;
						cur->bf = 1;
						break;     //由于旋转完的树的bf的值为-1，所以不用继续循环
					}
					
				}
				else if (cur->bf == -2)
				{
					if (cur->left->bf == 1)  // 先来一个左单旋 再来一个右单旋
					{
						Node* subL = cur->left;
						Node* subLR = subL->right;
						int _bf = subLR->bf;
						left_rotate(cur->left);
						right_rotate(cur);
						
						if (_bf == 1)
						{
							cur->bf = 0;
							subL->bf = -1;
						}
						else if (_bf == -1)
						{
							cur->bf = 1;
							subL->bf = 0;
						}
						else if (_bf == 0)
						{
							cur->bf = 0;
							subL->bf = 0;
						}

						cur = subLR->parent;
						prev = subLR;

						continue;
					}
					else if (cur->left->bf == -1)  //右单旋
					{
						right_rotate(cur);
						prev = cur->parent;
						cur = prev->parent;
						continue;
					}
					else if (cur->left->bf == 0)
					{
						right_rotate(cur);
						cur->bf = -1;
						cur->parent->bf = 1;
						break;
					}

				}
				if (cur && prev == cur->left)
				{
					(cur->bf)++;
				}
				else if (cur && prev == cur->right)
				{
					(cur->bf)--;
				}
			}
		}	
	};

}