KNN分类算法介绍，用KNN分类鸢尾花数据集（iris）

目录

一、KNN算法实现原理：

二、KNN算法实现步骤

三、KNN算法的优缺点

KNN算法的优点包括：

KNN算法在分类问题上的不足：

四、KNN分类鸢尾花数据集

1、构建KNN分类器

2、构建KNN模型

3、案例结果及分析

---

一、KNN算法实现原理：

        为了判断未知样本的类别，已所有已知类别的样本作为参照，计算未知样本与已知样本的距离，从中选取与未知样本距离最近的K个已知样本，根据少数服从多数的投票法则（Majority-Voting)，将未知样本与K个最近邻样本中所属类别占比较多的归为一类。以上即为KNN算法在分类任务中的任务原理。其中，K表示要选取的最近邻样本的实例的个数，可以根据实际情况进行选择。在sklearn库中，KNN算法的K值是通过n_neighbors参数来调节的，默认值为5。

二、KNN算法实现步骤

        KNN算法的实现分如下四步：

        （1）样本特征量化

        样本的所有特征都要做可比较的量化，若样本特征中存在非数值类型，则必须采取手段将其量化为数值。例如，样本的特征中包含颜色，可通过将颜色转换为灰度值来实现距离计算。

        （2）样本特征归一化

        样本有多个参数，每一个参数都有自己的定义域和取值范围，它们对距离计算的影响不一样，如取值较大的影响力会盖过取值较小的参数。所以，对样本参数必须做一些比例处理，最简单的方式即对所有特征的数值都采取归一化处置。

        （3）计算样本之间的距离

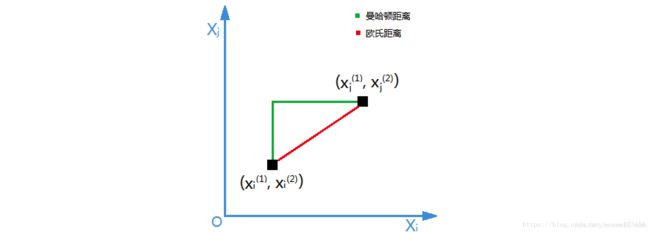
        需要一个距离函数以计算两个样本之间的距离，通常使用的距离函数有欧几里得距离（简称欧氏距离）、余弦距离、汉明距离和曼哈顿距离等，一般选欧氏距离作为距离度量，但是这些只适用于连续变量。在文本分类这种非连续变量情况下，汉明距离可以用来作为度量。通常情况下，如果运用一些特殊的算法来计算度量，K近邻分类准确率可显著提高，如运用大边缘最近邻法或者近邻成分分析法。

        下图展示了欧式距离与曼哈顿距离。

 

        （4）确定K值

        K值选得太大易引起欠拟合，太小容易过拟合，需交叉验证确定K值。

三、KNN算法的优缺点

KNN算法的优点包括：

        （1）简洁、易于理解、易于实现、无须估计参数，无须训练；

        （2）适合对稀有事件进行分类；

        （3）特别适用于多分类问题（Multi-label，对象具有多个类别标签）

KNN算法在分类问题上的不足：

        当样本不平衡时，即一个类的样本数量很大，而其它类样本数量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大数量类的样本容易占多数，导致错误分类。因此，KNN算法可以采用加权算法的方法来改进。比如，对样本距离小的邻域数据赋予更大的权值。

        KNN算法的主要使用场景包括文本分类、用户推荐等。

四、KNN分类鸢尾花数据集

1、构建KNN分类器

        首先获取鸢尾花数据集，对其划分训练集和测试集，然后通过绘制散点图，初步判断鸢尾花数据是否适合KNN分类。代码如下：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import pandas as pd
import mglearn 

# 加载鸢尾花数据集
iris = load_iris()

# 将数据集按照7:3的比例分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3, random_state=0)

# 导入数据集
iris_dataframe = pd.DataFrame(X_train,columns=iris.feature_names)
# 按y_train着色
grr = pd.plotting.scatter_matrix(iris_dataframe,c=y_train,figsize=(15,15),marker='o',hist_kwds={'bins':20},s=60,alpha=.8,cmap=mglearn.cm3)

         上图展示了鸢尾花数据散点分布。3种鸢尾花散点已经按照分类进行着色。可以很清晰地看到，现有数据基本上可以将3种花分类，各个颜色地散点基本可以形成群落。

2、构建KNN模型

        通过sklearn库使用Python构建一个KNN分类模型，步骤如下：

        （1）初始化分类器参数（只有少量参数需要指定，其余参数保持默认即可）；

        （2）训练模型；

        （3）评估、预测。

        KNN算法的K是指几个最近邻居，这里构建一个K = 3的模型，并且将训练数据X_train和y_tarin作为参数。构建模型的代码如下：

from sklearn.neighbors import KNeighborsClassifier
# 调用sklearn库中的KNN模型
knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train,y_train)

        注意，KNN是一个对象，knn.fit()函数实际上修改的是KNN对象的内部数据。现在KNN分类器已经构建完成，使用knn.predict()函数可以对数据进行预测，为了评估分类器的准确率，将预测结果和测试数据进行对比，计算分类准确率。

3、案例结果及分析

        调用2中构建的KNN模型进行预测，输出预测结果并计算准确率。代码如下：

import numpy as np
y_pred = knn.predict(X_test)
print("Test set predictions:\n{}".format(y_pred))
print("Test set core:{:.2f}".format(np.mean(y_pred == y_test)))

输出结果：

Test set predictions:
[2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0 2 1 0 2 2 1 0
 2 1 1 2 0 2 0 0]
Test set core: 0.98

从结果可知，KNN分类准确率达到了98%。