Leetcode刷题第二天数组--有序数组的平方,长度最小的子数组
leetcode60天刷题打卡第二天,数组理论
-
- 有序数组的平方
- 长度最小的子数组
- 螺旋矩阵II
有序数组的平方
题目:给你一个按非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
第一种求解思路是暴力排序:用一个for循环将nums的元素全部平方,再用sort进行排序
class Solution{
public:
vector<int> sortedSquares(vector<int>& nums){
for(int i = 0; i < nums.size(); i++){
nums[i] *= nums[i];
}
sort(nums.begin(), nums.end());
return nums;
}
};
第二中思路是基于双指针。因为数组是非递减排序的数组,所以平方后的最大值肯定优先出现在一头一尾,自然就想到通过使用一头一尾两个指针,对首尾进行比较,大的放入新的数组尾部,然后移动指向大数值的指针,继续进行比较。
class Solution{
public:
vector<int> sortedSquares(vector<int>& nums){
int leftIndex = 0;
int rightIndex = nums.size() - 1;
vector<int> temp(nums.size(), 0);
int Index = nums.size() - 1;
while(leftIndex <= rightIndex){ //这里用<=是因为要当=是要将指向的数值进行赋值到新的数组中
if(nums[leftIndex] * nums[leftIndex] < nums[rightIndex] * nums[rightIndex]){
temp[Index] = nums[rightIndex] * nums[rightIndex];
Index--;
rightIndex--;
}else{
temp[Index] = nums[leftIndex] * nums[leftIndex];
Index--;
leftIndex++;
}
}
nums = temp;
return nums;
}
};
自己写的代码感觉冗余内容较多,下面是别人写的代码,思想是一样的,但代码看着更加简洁。
class Solution{
public:
vector<int> sortedSquares(vector<int>& nums){
int Index = nums.size() -1;
vector<int> result(nums.size() ,0);
for(int i = 0, j = nums.size() - 1; i <= j;){
if(nums[i] * nums[i] < nums[j] * nums[j]){
result[Index--] = nums[j] * nums[j];
j--;
}else{
result[Index--] = nums[i] * nums[i];
i++;
}
}
nums = result;
return nums;
}
};
长度最小的子数组
题目:给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例2:
输入:target = 4, nums = [1,4,4]
输出:1
示例3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
第一种思路当然又是暴力解法,暴力解法的思想是基于每个元素做为起始位置循环去寻找满足条件的子数组,用两个for循环来不断查找满足条件的子数组,并不断的比较子数组的长度。第一个for循环代表起始位置,第二for循环做的事情是在该起始位置下满足条件子数组的长度是多少,并更新结果。
class Solution{
public:
int minSubArrayLen(int target, vector<int>& nums){
int result = INT32_MAX;
int sum = 0;
int subLength;
for(int i = 0; i < nums.size(); i++){
sum = 0;
for(int j = i; j < nums.size(); j++){
sum += nums[j];
if(sum >= target){
subLength = j - i +1;
result = result < subLength ? result : subLength;
break;
}
}
}
return result == INT32_MAX ? 0 : result;
}
};
第二种思路是滑动窗口,该思想是基于一个类似窗口的操作去寻找满足条件的子数组,当一个窗口满足条件后,通过把窗口起始位置向前移动一位再计算窗口是否满足条件来进行滑动,若不满足,再将窗口尾部向后滑动。
class Solution{
public:
int minSubArrayLen(int target, vector<int>& nums){
int result = INT32_MAX;
int sum = 0;
int subLength;
int i = 0;
for(int j = 0; j < nums.size(); j++){
sum += nums[j];
while(sum >= target){
subLength = j - i + 1;
result = result < subLength ? result : subLength;
sum -= nums[i++];
}
}
return result == INT32_MAX ? 0 : result;
}
};
螺旋矩阵II
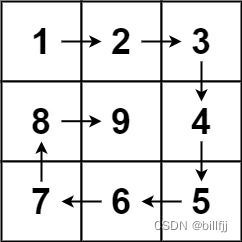
题目:给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例2:
输入:n = 1
输出:[[1]]
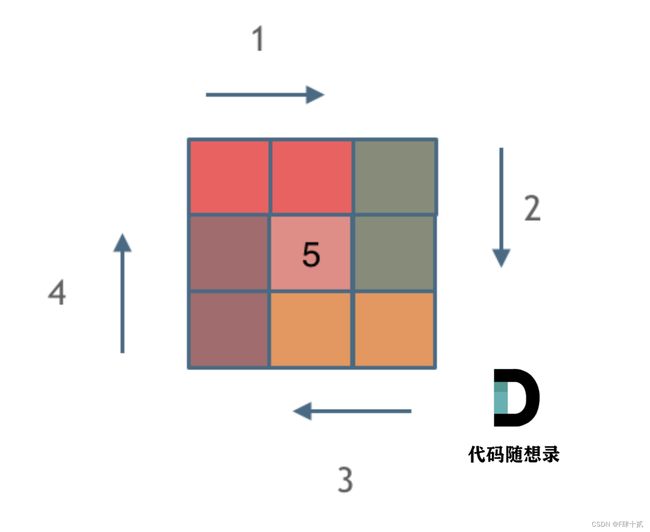
关于螺旋矩阵,主要首先观察其规律,第一n要分奇偶,当n为奇数时,我们需要单独处理最后矩阵中心的数值,当n为偶数时,我们就不需要处理中心值了。第二是循环的圈数,我们不难发现循环的圈数loop = n / 2(当n为基数时,我们单独处理中心的数值所以先不考虑中心值)。第三是每圈循环边长的时候要注意统一区间,如左闭右开,保持一致。第四是每一圈在处理边长时需要遍历的长度,因为我们选择的是左闭右开区间,所以每次将最后一个数值交给下一个循环去做,用偏移量来描述就是每圈的offset += 1。
class Solution{
public:
vector<vector<int>> generateMatrix(int n){
vector<vector<int>> res(n,vector<int>(n, 0));
int startx = 0, starty = 0;
int loop = n / 2;
int mid = n / 2;
int offset = 1;
int count = 1;
int x, y;
while(loop--){
x = startx;
y = starty;
for(; y < n - offset; y++){
res[x][y] = count++;
}
for(; x < n - offset; x++){
res[x][y] = count++;
}
for(; y > starty; y--){
res[x][y] = count++;
}
for(; x > startx; x--){
res[x][y] = count++;
}
startx++;
starty++;
offset++;
}
if(n % 2){
res[mid][mid] = count;
}
return res;
}
};