PID算法
目录
- 前言
- 一、PID算法简介
-
- 1.1 比例环节( Proportion)
- 1.2 积分环节(Integral)
- 1.3 微分环节(Differential)
- 二、PID算法离散公式
-
- 2.1 位置式 PID 公式(或全量式 PID 公式)
- 2.2 增量式 PID 公式
- 2.3 两种公式的不同点
- 2.4 两种公式的优缺点
- 2.5 积分饱和问题
- 三、PID 算法代码实现
-
- 3.1 控制量相关的结构体
- 3.2 PID 算法代码
- 四、PID 参数整定
-
- 4.1 采样周期选择
- 4.2 理论计算整定法
- 4.3 工程整定法
-
- 4.3.1 试凑法
- 4.3.2 临界比例法
- 4.3.3 一般调节法
- 五、电机控制PID使用方法
-
- 5.1 速度环PID控制
- 5.2 电流环PID控制
- 5.3 位置环PID控制
- 5.4 三环PID控制原理
前言
介绍一下什么是PID,以及基本实现和注意事项
一、PID算法简介
PID 算法是闭环控制系统中常用的算法,PID 分别是 Proportion(比例)、Integral(积分)、Differential(微分)的首字母缩写。它是一种结合比例、积分和微分三个环节于一体的闭环控制算法。在闭环控制系统中,引入了反馈回路,利用输出(实际值)和输入(目标值)的偏差,对系统进行控制,避免偏离预定目标。闭环控制系统又称反馈控制系统具体的控制流程如下图所示:

1.1 比例环节( Proportion)
比例环节可以成比例地反应控制系统的偏差信号,即输出与输入偏差成正比,可以用来减小系统的偏差。此环节的公式如下:

- u — 输出
- Kp — 比例系数
- e — 偏差
假设我们现在需要调节棚内温度为 30℃,而实际温度为 10℃,此时的偏差 e=20,由比例环节的公式可知,当 e 确定时,Kp 越大则输出u 越大,也就是温控系统的调节力度越大,这样就可以更快地达到目标温度;而当 Kp 确定时,
偏差 e 越大则输出 u 越大。由此可见,在比例环节中,比例系数 Kp 和偏差 e 越大则系统消除偏差的时间越短

当 Kp 的值越大时,其对应的橙色曲线达到目标值的时间就越短,与此同时,橙色曲线出现了一定幅度的超调和振荡,这会使得系统的稳定性下降,因此,我们在设置比例系数的时候,并不是越大越好,而是要兼顾消除偏差的时间以及整个系统的稳定性
1.2 积分环节(Integral)
在实际的应用中,如果仅有比例环节的控制,可能会给系统带来一个问题:静态误差。静态误差是指系统控制过程趋于稳定时,目标值与实测值之间的偏差
假设我们现在需要调节棚内温度为 30℃,而实际温度为 25℃,此时偏差 e=5,Kp 为固定值,如果此时的输出可以让大棚在半个小时之内升温 5℃,而外部的温差可以让大棚在半个小时之内降温 5℃,也就是说,输出 u 的作用刚好被外部影响抵消了,这就使得偏差会一直存在

积分环节可以对偏差 e 进行积分,只要存在偏差,积分环节就会不断起作用,主要用于消除静态误差,提高系统的无差度。引入积分环节后,比例+积分环节的公式如下:

从上述公式中可以得知,当积分系数 Ki 或者累计偏差越大时,输出就越大,系统消除静态误差的时间就越短

只要系统还存在偏差,积分环节就会不断地累计偏差。当系统偏差为 0的时候,说明已经达到目标值,此时的累计偏差不再变化,但是积分环节依旧在发挥作用(此时往往作用最大),这就很容易产生超调的现象了。因此,我们需要引入微分环节,提前减弱输出,抑制超调的发生。
1.3 微分环节(Differential)
微分环节的作用是反应系统偏差的一个变化趋势,也可以说是变化率,可以在误差来临之前提前引入一个有效的修正信号,有利于提高输出响应的快速性, 减小被控量的超调和增加系统的稳定性。引入微分环节后,比例+积分+微分环节的公式如下:

该公式是 PID 离散公式之一,大家需要注意,在实际的应用中,并不是每一个系统都需要 PID 的三个环节参与控制的,有的系统只需要比例环节或积分环节就可以控制得很好。
微分环节有助于系统减小超调,克服振荡,加快系统的响应速度,减小调节时间,从而改善了系统的动态性能,但微分时间常数过大,会使系统出现不稳定。微分控制作用一个很大的缺陷是容易引入高频噪声,所有在干扰信号比较严重的流量控制系统中不宜引入微分控制作用。
二、PID算法离散公式
2.1 位置式 PID 公式(或全量式 PID 公式)

在上一小节中得到的 PID 离散公式称为位置式或全量式 PID 公式,该公式的计算需要全部控制量参与,它的每一次输出都和过去的状态有关
2.2 增量式 PID 公式
通过位置式的 PID 公式,我们只需两步即可推导出增量式 PID 公式:
①将 k = k-1 代入位置式 PID 公式,得:

②由 -−1 得:
![]()
2.3 两种公式的不同点
| 对比相 | 位置式 | 增量式 |
|---|---|---|
| 输出 | 全量输出 | 仅输出增量 |
| 偏差 | 需要一直累计偏差 | 只考虑最近 3 次偏差 |
| 积分作用 | 有 | 无 |
| 限幅 | 需要进行输出和积分限幅 | 只需要进行输出限幅 |
2.4 两种公式的优缺点
①位置式
优点:位置式 PID 是一种非递推式算法,可直接控制执行机构(如平衡小车),u(k) 的值和执行机构的实际位置(如小车当前角度)是一一对应的,因此在执行机构不带积分部件的对象中可以很好应用;
缺点:: 每次输出均与过去的状态有关,计算时要对 e(k) 进行累加,运算工作量大
②增量式
优点:只输出增量,计算错误影响小;不需要累计偏差,运算量少,实时性相对较好。
缺点:积分截断效应大,有稳态误差;溢出的影响大。有的被控对象用增量式则不太好;
2.5 积分饱和问题
在位置式 PID 中,如果系统长时间无法达到目标值,累计偏差(积分)就会变得很大,逐渐达到深度饱和的状态此,时系统的响应就很慢了。

为了避免位置式 PID 中可能出现的积分饱和问题,可采取以下措施:
① 优化 PID 曲线,系统越快达到目标值,累计的偏差就越小;
② 限制目标值调节范围,规避可以预见的偏差;
③ 进行积分限幅,在调整好 PID 系数之后,根据实际系统来选择限幅范围。
三、PID 算法代码实现
3.1 控制量相关的结构体
/* PID相关参数 */
#define INCR_LOCT_SELECT 0 /* 0:位置式 ,1:增量式 */
#if INCR_LOCT_SELECT
/* 增量式PID参数相关宏 */
#define KP 8.50f /* P参数*/
#define KI 5.00f /* I参数*/
#define KD 0.10f /* D参数*/
#define SMAPLSE_PID_SPEED 50 /* 采样周期 单位ms*/
#else
/* 位置式PID参数相关宏 */
#define KP 10.0f /* P参数*/
#define KI 6.00f /* I参数*/
#define KD 0.5f /* D参数*/
#define SMAPLSE_PID_SPEED 50 /* 采样周期 单位ms*/
#endif
/* PID参数结构体 */
typedef struct
{
__IO float SetPoint; /* 设定目标,用于偏差计算 */
__IO float ActualValue; /* 期望输出值 */
__IO float SumError; /* 误差累计 */
__IO float Proportion; /* 比例常数 P */
__IO float Integral; /* 积分常数 I */
__IO float Derivative; /* 微分常数 D */
__IO float Error; /* Error[1] */
__IO float LastError; /* Error[-1] */
__IO float PrevError; /* Error[-2] */
} PID_TypeDef;
3.2 PID 算法代码
int32_t increment_pid_ctrl(PID_TypeDef *PID,float Feedback_value)
{
PID->Error = (float)(PID->SetPoint - Feedback_value); /* 计算偏差 */
#if INCR_LOCT_SELECT /* 增量式PID */
PID->ActualValue += (PID->Proportion * (PID->Error - PID->LastError)) /* 比例环节 */
+ (PID->Integral * PID->Error) /* 积分环节 */
+ (PID->Derivative * (PID->Error - 2 * PID->LastError + PID->PrevError)); /* 微分环节 */
PID->PrevError = PID->LastError; /* 存储偏差,用于下次计算 */
PID->LastError = PID->Error;
#else /* 位置式PID */
PID->SumError += PID->Error;
PID->ActualValue = (PID->Proportion * PID->Error) /* 比例环节 */
+ (PID->Integral * PID->SumError) /* 积分环节 */
+ (PID->Derivative * (PID->Error - PID->LastError)); /* 微分环节 */
PID->LastError = PID->Error;
#endif
return ((int32_t)(PID->ActualValue)); /* 返回计算后输出的数值 */
}
increment_pid_ctrl 函数用来进行位置式 PID 的控制,该函数的 2 个形参:*PID 传入 PID控制量相关的结构体地址;Feedback_value 传入当前系统的实际值,用于计算偏差。在函数中,我们先计算本次偏差 Error,然后把偏差累计,存入 SumError 成员当中,接着根据位置式的公式进行三个环节的计算,计算后的期望输出存入 ActualValue 成员当中,然后存储本次偏差,最后返回期望输出值。
四、PID 参数整定
PID 参数整定的方法很多,概括起来有两大类:理论计算整定法和工程整定法
4.1 采样周期选择
采样周期指的是 PID 控制中实际值的采样时间间隔,其越短,效果越趋于连续,但对硬件资源的占用也越高。在实际的应用中,我们可以使用理论或者经验方法来确定采样周期:
① 理论方法:香农采样定理。这个定理可以用来确定采样周期可选择的最大值,当采样周期超出了这个最大的允许范围,我们所得到的信号就会失真,也就无法较好地还原信号了。
② 经验方法:根据控制对象突变能力选择。假设电机当前转速为 20RPM,我们需要提高它的转速到 30RPM,此电机的转速在 1s 之内最大可以突变 10RPM(即电机速度的突变能力),如果我们每 1ms 采集一次电机转速,那么每一次采集到的速度变化量最大为 10RPM / 1000 = 0.01RPM,很明显,此时最大的变化量远远小于当前的速度,这对于我们的 PID 控制效果并没有明显的提升,但是却占用了很多的硬件资源,因此,我们需要根据控制对象的突变能力来选择采样周期。
4.2 理论计算整定法
依据系统的数学模型,经过理论计算确定 PID 参数。这种方法是建立在理想化条件下的,其得到的参数不一定能够直接使用,还需要结合经验以及实际的系统进行调整。
4.3 工程整定法
4.3.1 试凑法
- 方法:结合系统的具体情况以及经验,先试凑几组合理的 PID 系数,同时需要观察系统的曲线变化,确定每一个系数对于整个系统曲线的大致影响,然后再根据具体的曲线进行调整。
- 步骤:
① 先是比例(P),再积分(I),最后是微分(D);
② 按纯比例系统整定比例系数,使其得到比较理想的调节过程曲线,然后再把比例系数缩小 1.2 倍左右,将积分系数从小到大改变,使其得到较好的调节过程曲线;
③ 在这个积分系数下重新改变比例系数,再看调节过程曲线有无改善;
④ 如有改善,可将原整定的比例系数减少,改变积分系数,这样多次的反复,就可得到合适的比例系数和积分系数;
⑤ 如果存在外界的干扰,系统的稳定性不好,可把比例、积分系数适当减小,使系统足够稳定;
⑥ 如果系统存在小幅度超调,可以将整定好的比例系数和积分系数适当减小,增大微分系数,以得到超调量最小、调节作用时间最短的系统曲线;
4.3.2 临界比例法
- 方法:在闭环的控制系统里,将调节器置于纯比例作用下,从小到大逐渐调节比例系 数,直到系统曲线出现等幅振荡,再根据经验公式计算参数。
- 步骤:
① 将积分、微分系数置零,比例度取适当值,平衡操作一段时间,使控制系统按纯比例作用的方式投入运行。
② 慢慢地增大比例系数,细心观察曲线的变化情况。如果控制过程的曲线波动是衰减的,则把比例系数继续增大;如果曲线波动是发散的,则应把比例系数减小,直至曲线波动呈等幅振荡,此时记下临界比例系数 δK 和临界振荡周期 Tk 的值。
③ 根据记下的比例系数和周期,采用经验公式,计算调节器的参数。
| 参与控制的环节 | Kp | Ki | Kd |
|---|---|---|---|
| P | δK/2 | 0 | 0 |
| PI | δK/2.2 | Kp/(0.833·Tk) | 0 |
| PID | δK/1.7 | Kp/(0.5·Tk) | 0.125·Tk·Kp |
4.3.3 一般调节法
- 方法:这种方法针对一般的 PID 控制系统所以称之为一般调节法。
- 步骤:
① 首先将积分、微分系数置零,使系统为纯比例控制。控制对象的值设定为系统允许的最大值的 60%~70%,接着逐渐增大比例系数,直至系统出现振荡;此时再逐渐减小比例系数,直至系统振荡消失,然后记录此时的比例系数,并设定系统的比例系数为当前值的 60%~70%。
② 确定比例系数后,设定一个较小的积分系数,然后逐渐增大积分系数,直至系统出现振荡;此时在逐渐减小积分系数,直至系统振荡消失,然后记录此时的积分系数,并设定系统的积分系数为当前值的 55%~65%。
③ 微分系数一般不用设定,为 0 即可。若系统出现小幅度振荡,并且通过 PI 环节无法优化,这可以采用与确定比例、积分系数相同的方法,微分系数取系统不振荡时的 30%左右。
④ 系统空载、带载联调,再对 PID 参数进行微调,直至满足要求。
五、电机控制PID使用方法
5.1 速度环PID控制
我们只需要把 PID 控制流程中的控制对象换成电机速度即可,先设置目标转速,系统会计算出偏差 e,然后将偏差输入到 PID 控制的三个环节中,PID 计算后的输出值用于控制 PWM 的占空比,进而控制电机的速度。
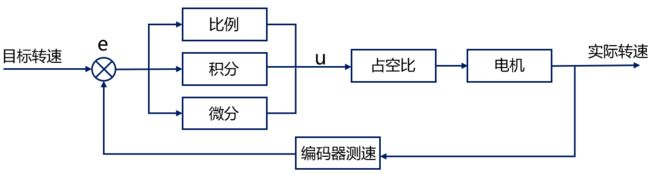
注意:PID输出的是PWM占空比,而不是速度本身
5.2 电流环PID控制
电流环 PID 控制的原理非常简单,只需要把 PID 控制流程中的控制对象换成电机电流。我们先设置目标电流,系统会计算出偏差 e,然后将偏差输入到 PID 控制的三个环节中,PID 计算后的输出值用于控制 PWM 的占空比,进而控制电机的电流。

5.3 位置环PID控制
同理,位置环 PID 控制就是用编码器计数总值代表电机的位置,然后把 PID控制流程中的控制对象换成电机位置即可。我们首先设置目标位置,系统会计算出偏差 e,然后将偏差输入到 PID 控制的三个环节中,PID 计算后的输出值用于控制 PWM 的占空比,进而控制电机的位置。
位置环主要使用位置式PID进行计算,作用是在特定位置启停

5.4 三环PID控制原理
三环 PID 控制就是将三个 PID 控制系统(例如:电流环、速度环以及位置环)串联起来,然后对前一个系统(外环)的输出进行偏差的计算,计算结果作为后一个系统(内环)的输入

电机位置是优先控制的对象,三环 PID 控制的流程如下:
① 首先设置目标位置,系统会计算出位置偏差,然后将偏差输入到位置环(最外环);
② 位置环的输出和实际速度进行偏差的计算,计算后的偏差输入到速度环(次外环);
③ 速度环的输出和实际电流进行偏差的计算,计算后的偏差输入到电流环(内环),电流环的输出用于控制 PWM 的占空比,进而控制电机的位置。
