二进制与位运算基础

  不管是编程入门还是算法的学习，二进制与位运算都是必备技能，但在很多视频或教材里却总是轻描淡写或者以“用不到”为由去淡化其讲解。虽然在如今的编译器中加减乘除运算已经和位运算没什么性能差距，但很多网上的文章在进行大数据量计算时还是习惯采用位运算的方法~~(其实就是耍帅)~~，而像树状数组用到的lowbit就更是位运算中的重要知识点，所以本章将会把常用的知识进行讲解，且面向人群较广保证所有人都可以听懂。

通过本章的学习你可以：

1. 学会二进制与十进制的互相转换
2. 了解 &、|、^、~、<<、>>位运算符的原理
3. 学会运用一些简单的位运算操作
4. 清楚lowbit的原理
5. 理解快速幂算法模板

一、二进制与十进制整数的相互转化

  在讲转化之前再简单的说一下进制的问题，所谓进制其实就是逢几进一，我们平常用的十进制其实就是逢十进一，数字范围是从0-9，二进制则为逢二进一，数字范围是0-1。

1.十进制转二进制（短除法）

  其实短除法算是十进制转P进制的通用方法，其原理就是用十进制数X不断与P相除并记录他的余数，最后将余数逆序串在一起得到的则是对应的P进制数，文字说起来可能比较难懂，我们举一个例子应该就明白了：

在例子中为求得十进制下的18转化为二进制的值，我们把18不断的与2相除并保存其余数，最后从尾到头将余数连起来则得到了二进制数：10010，方法还是简单易懂的，大家可能自己举例练习。

2.二进制转十进制（按权展开加和）

  在讲解之前我们先说一下什么是位权，在定义上：位权指数制中每一固定位置对应的单位值，通俗的来讲，其实就是每一位的权值，一般等于 P^i-1，以十进制下的1000(千位数)来举例，第一位(个位)的位权是1，第二位为10，第三位为100，第四位为1000。而二进制转十进制则是先将位权展开与其对应的值相乘，最后再将这个值相加起来得到的则是对应的十进制表示。我们以二进制下的 10010011为例。

按权展开加和即为：1 x 2⁰ + 1 x 2¹ + 1 x 2²+ 1 x 2³+ 1 x 2⁴+ 1 x 2⁵+ 1 x 2⁶+ 1 x 2⁷ = 1 + 2 + 0 + 0 + 16 + 128 = 147；

这就是二进制转十进制的过程，同样也是P进制转十进制的通用方法，大家可以自己举例进行练习。

二、常用的位运算

  我们都知道计算机是用二进制来进行存储和计算的，而计算机通过操作二进制数来进行运算的操作则为位运算，我们平常使用的算术运算符其实就是对位运算进行了转化，位运算包括：按位与(&)、按位或(|)、按位异或(^)、按位取反(~)、左移(<<)、右移(>>)，接下来我也将依次说明每个运算符的用处。

注：因为本文章只是入门基础，所以更底层的知识并未详细讲解，在没有很深刻认识的情况下还是建议在不必要的情况下用普通的算数运算符来计算，位运算符可能会出现很多问题。

1.按位与(&)

  按位与遵循这一个规则：两个二进制数的对应的每一位若都是1则为1，否则为0.

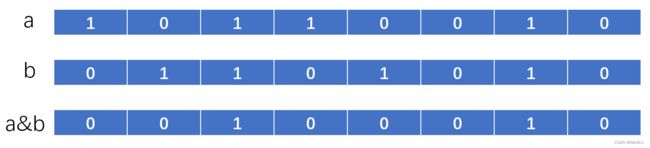
  我们来举个例子，a的二进制表示为10110010，b的二进制表示为01101010，那么a & b的运算过程则为下图所示：

通过计算器验证后也可以说明我们的方法是正确的，这就是按位与运算的规则，那下面我们来看下它的实际应用：

a.判断一个数是否为2的整数幂

  通过前面说过的二进制的机制我们不难发现，如果一个数是2的整数幂，那么在这个数对应的二进制中有且仅有一个1，并且1一定是这个数的最高位(其实就是位权)，当我们将这个数减1时就会发现除了最高位以外其他位全部变为1，最高位为0，这个时候将两个数进行按位与运算操作，若结果为0则是2的整数幂，反之则不是。简单举一个例子：

实现代码如下：

bool mi(int n){
    if(n & (n - 1)) return false;
    return true;
}

b.计算一个二进制中1的个数

  其实这个有多种方法，而其中一种因为涉及到移位运算所以我们暂时先不说。在只用过按位与运算的情况下，我们设输入的数字为num，每次做 num & (num-1)操作并将其值赋值给num，一直循环到num为0为止，循环几次则说明二进制中有几个1.这个方法可能很多人第一次看的时候会比较懵，实际上做减一操作无非就有两种情况：

 1.末位为1，减一后变为0；

 2.末位为0，需向前位借位，最后为1

通过这种方式我们就会发现，两个数每次做位与运算时都会稳定的消除一个1，依次类推最后可以求出二进制中1的个数，最终实现代码如下：

int func(int num){
    int cnt = 0;
    while(num){
        num = num & (num - 1);
        cnt++;
    }
    return cnt; 
}

2.按位或(|)

  按位或遵循这样的规则：两个二进制数的对应的每一位只要有一个是1则为1，都是0则为0.

  我们同样来举一个例子，a与b的二进制值同上，接下来我们来计算a | b的值，计算过程如下图：

同样通过计算机验证了我们结果的正确性，但在实际中用按位的场景并不多，接下来来简单举一个用到按位或的场景：

a.线段树访问右子树

  如果学过线段树的同学，在操作中一定有见过这个符号，以建树操作为例：

void build(int u,int l,int r){
    tree[u].l = l;
    tree[u].r = r;
    if(l == r){
        tree[u].w = a[l];
        return;
    }
    int mid = l+r >> 1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
    pushup(u);
}

在递归建树的过程中同时用到了左移运算符和按位或运算，左移1位我们后面会说它的效果与乘2一样，而在后面加“|1”的意义则是因为一个数不管奇偶与2相乘一定为偶数，若为偶数那么其二进制表示中最低位就一定为0，那么此时我如果想+1则可以直接通过“|1”来实现。

3.按位异或(^)

  异或的运算规则与按位或很相似：同零为0，相异为1，但同1为0。

  我们继续用刚才的数据来举例：

通过计算我们也验证了其正确性，但在讲解应用之前，我们先要来了解一下按位异或的一些性质：

 1. 按位异或可以将某些位取反，但如果连续异或两次将变为原值，比如：a ^ b ^ b = a；

 2. 0异或任何数都为任何数 (0 ^ 0 = 0，0 ^ 1 = 1)；

 3. 1异或任何数都会使任何数取反 (0 ^ 1 = 1，1 ^ 1 = 0)；

 4. 任何数异或自己都为0 (0011 ^ 0011 = 0)；

 5. 交换律：a ^ b = b ^ a；

 6. 结合律：(a ^ b) ^ c = a ^ (b ^ c)

可以发现异或的性质还是很多的，其实平常用的场景也比较多，这里就给大家列举几个最经典的场景：

a.不引入第三个变量交换两个数

实现代码很简单：

a = a ^ b;
b = b ^ a;
a = a ^ b;	

是不是第一眼看起来很懵，其实我们可以拆开分析，第一句没什么好说的，第二句b = b ^ a我们完全可以等效成 b = b ^ a ^ b，又根据交换律可得b = b ^ b ^ a，因此b将自己置零并获得a的值(由性质2和性质4)，第三句中则可等效为 a = a ^ b = a ^ b(曾经) ^ b(现在) = a ^ b（曾经）^ a = a ^ a ^ b = b。可能第一次看比较晕，可以后面自己去推导一下。

b.与特定位翻转

根据上面说过的性质2与性质3，我们就完全可以将特定位的二进制设为1，其他位为0，并将这个二进制数与目标数进行异或运算，比如：对 10100001 的第2位和第3位进行翻转，那么我们可以设另一个二进制数为10100001进行异或运算，即可达成我们想要的效果。

c.汇编语言变量置零：xor a, a

思考：如何用 ^ 和 & 来实现 | 操作？

4.按位取反(~)

  按位取反是一个一元运算符，它的运算规则还是比较麻烦的，在讲解之前我们需要简单提一下三个概念：原码、反码和补码。(因与本次讲解的章节联系不大所以只是简单说说，想详细了解请看专业文章)

其实简单来讲这三个码其实就是三种不同的编码方式，其中可以概括为两大类：

 1.当数为正数时：原码为自己本身的二进制码，符号位为0，反码与补码都等于原码；

 2.当数为负数时：

  原码：为自己本身的二进制码，但最前的符号位为1，代表负数

  反码：符号位保持不变，其余位取反

  补码：在反码的基础上+1

而在这里可以先告诉各位一个结论，在C++中负数以补码的形式存储。

  经过了前面的铺垫，我们也可以说一下按位取反的规则：

   1.当数为正数时，将原码取反(包括符号位)，再将原码转化为补码，得到的就是该数取反的值，我们以8举例：

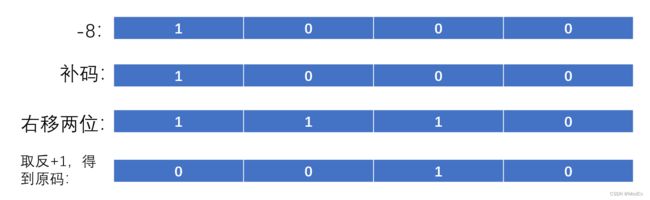
   2.当数为负数时，先转化为对应的补码，将补码取反(包括符号位)，得到的就是该数按位取反的值，我们以-8举例：

所以通过举例我们也发现了规律，对于按位取反而言取反后的值等于原值+1的相反数。

5.移位运算( << >>)

  这就顾名思义了，将一个数移动多少位，只不过这里的移动指的是在二进制下的移动，移位运算分为两种，左移和右移：

左移：

  把对应数字的二进制码向左移动n位，左边溢出的部分直接删除，右边的空位补0，具体演示如下图：

关于溢出：常用的int类型变量为32位整数，我们平常在表示二进制的时候为了方便只表示出有意义的部分，实际在内存中前面未使用的部分都是用0来填充，所以溢出指的是在内存中的位而不是数字有意义的位。

对于移位：若移位超出了存储变量的位数，会自动对其取模，比如32位变量中，若移动34位，则实际移动位数为 34 % 32 = 2。

右移：

  对于右移而言就要稍微麻烦一些，在右移时如果为正数则左边的空位补0，如果为负数则补1，简单来说就是空下来的位补其对应的符号位，右侧移出部分则直接删除，正数应该没什么好说的，主要是是在于负数，这里也用一张图来表示：

应用：快速乘或除2的n次方

  通过前面所说的二进制知识在结合移位运算的原理，我们不难看出，在左移时若没有干扰到存储数据中有意义的部分，则得到的值为原值乘2的n次方，右移时则为除2的n次方，这里的除若出现余数则直接向下取整，演示效果如下：

int n = 8;
cout << (n << 2) << endl;//32
cout << (n >> 2) << endl;//2

三、应用：lowbit运算

  lowbit运算算是二进制与位运算中最大的一个应用，也是学习树状数组的一个重要前置芝士。它的作用是用来得到数字n在二进制表示下最低位的1以及它后面的0构成的数值，举个例子：88的二进制表示为01011000，那么lowbit(88) = (1000)₂。这种运算应该怎么实现呢？

算法原理：

  首先假设最低位的1在第k位，此时我们对这个数进行取反，取反后第k位会从1变为0，而在第k位之前则全部为1，我们根据取反的规则现在所有位与原数相比都是不同的，换句话说设这个数为a，则a & ~a = 0，我们把取反的数+1，那么因为第k位之前现在全部为1，第k位为0，+1后第k位之前全部变为0，第k位变为1，此时再与原数做按位与运算就可以得到最低位的1及后面0构成的值。可以根据下图帮助理解一下：

其实通过按位取反运算的规律：n = -(n+1)我们也能发现，对于这个取反加1步骤而言其实就是把转化为了其相反数，所以我们也完全可以通过 x & (-x)来得到我们想要的值，最后就是代码实现部分了，这里给出两个版本的实现代码：

int lowbit(int x){
	return (x & -x);
}

int lowbit(int x){
    return (n & (~n + 1));
}

四、快速幂(反复平方法)

  最后我们来说一下快速幂，快速幂也叫反复平方法，见名之意其作用其实就是有着比普通方法求幂次方更高的效率，但具体会应用在哪些场景里，我们先看下面这道题：

给定n组 a_i，b_i，p_i，对于每组数据，求出a_i^b_i mod p_i 的值。

数据范围

1 ≤ n ≤ 100000

1 ≤ a_i，b_i，p_i ≤ 2 x 10⁹

如果按照以前的方法，那么a_i^b_i则需要从1枚举到b_i，时间复杂度为O(n * b)，很显然会超时，那么我们还有没有其他的方法，能把运算次数降下来呢？

  来举一个例子，假如a为2，b为4，p为1，按照平常暴力的写法则是2x2x2x2，需要运算4次，但我们不难发现这可以化简成(2²)²这样只需要运算两次就可以达成我们的目的，再举一个例子，a为2，b为13，p为1，那么可以把问题拆成2¹ · 2⁴ · 2⁸，那么知道这几个数的值也可以通过以前已经获得的值来求得新的值，比如2⁴ = (2²)²，计算次数就会大幅降低，那么我们应该怎么来进行拆分呢？

  我们将幂转化为二进制，即要求2¹¹⁰¹的值，那么根据前面的位权讲解，2¹¹⁰¹ = 2¹ · 2¹⁰⁰ · 2¹⁰⁰⁰，再转化为十进制则和上述所说一样，对于指数而言则是可以化为2¹、2²、2³，所以我们可以得出一个结论：对于任何一个十进制数，都可以用多个2^k相乘来表示，那么接下来就很容易了，我们对于求解a^k而言，我们只需将它拆成a^k1·a^k2·····a^kn = a^k，后面的幂次方可以由前面的值推出来，推导的方法则是在前位的基础上做一个平方操作（因为每一位都是用2^x表示，想要得到后一位的值直接对原先的数平方即可），从而得出下一位的值，若下一位的值为0则不作操作，若为1则将对应的值与我们将要得到的结果相乘，以此类推。

  也许文字还是比较难懂，所以在这里演示了一个过程，方便大家理解：

例：求3¹⁰，将指数转化为二进制表示为：3¹⁰¹⁰，将底数存储变量a，最终结果为res。

1.判断该二进制第一位是否为1——1010---->0，因为第一位为0所以res不做操作，a变为其平方倍，即a *= a，此时变为9；

2.将指数右移一位，判断该二进制数第一位是否为1——0101—>1，则res *= a，a变为其平方倍，即a *= a，此时a为81；

3.与之前同理，右移判断第一位是否为1——0010—>0，所以res不做操作，a *= a，此时a为6561；

4.再次右移并判断，此时仅剩最后一位且为1，这时res *= a，a变为平方倍(其实这里可以直接跳出了)，得到结果59409，通过验证与预期结果相符。

在这个方法中循环求解的次数取决于指数的实际长度，即对于求解a^k，我们在这之中要依次得到a²¹、a²²、a²³·····a^2logk，很显然时间复杂度为O(logk)，这里的k指的是输入的指数，很明显通过这个方法效率得到了很大的提升，说了这么多后我们再回归到之前的题目：求解a_i^b_i mod p_i 的值，其实和我们刚才举得例子基本相同，只是需要每一步都需要对p_i取模，那么我们根据上面的一系列分析，写出最终的代码：

#include 
using namespace std;

typedef long long ll;

ll qmi(int a,int b,int p){
    ll res = 1 % p;
    while (b)
    {
        if(b & 1) res = res * a % p;
        a = a * (ll)a % p;
        b >>= 1;
    }
    return res;

}

int main() {
    int n;
    scanf("%d",&n);
    for(int i = 1;i<=n;i++){
        int a,b,p;
        scanf("%d %d %d",&a,&b,&p);
        printf("%lld\n",qmi(a,b,p));
    }
    return 0;
}

这样这道题就是求解完成了，这也是快速幂的算法原理，在之后的题目中若出现像这道题一样指数值极大的情况下可以考虑使用快速幂，通过这个算法也相信对前面的二进制与位运算有更深刻的理解。

五、总结

  在本章中讲了二进制与位运算的基础，实际的数制与位运算远比今天讲的要复杂得多，大家感兴趣的可以去查看相关资料，相信在本章中加深了各位对计算机底层知识的理解。

---

  好了本期内容到这里就结束了，如果你认为该文章对你有一点点帮助，也请希望点个关注或者关注微信公众号：ModCx，如果有什么疑问或者建议也可在微信公众号后台留言，你们的支持就是我的动力，让我们下期再见~