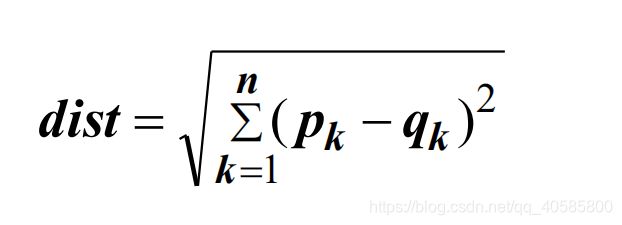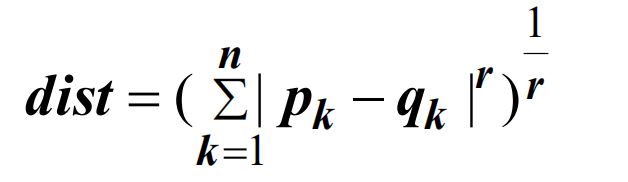数据和数据预处理（ML&DM）

Data & Data Preprocessing

---

---

1. 数据 & 属性

数据：数据对象及其属性的集合

属性：属性是对象的属性或特征

属性值：属性值是分配给属性的数字或符号

属性和属性值的区别：

• 相同的属性可以映射到不同的属性值

• 不同的属性可以映射到同一组值

1.1 属性的类型

1.1.1 根据属性特征划分

属性的类型取决于它所拥有的数字的下列哪些操作：

• Distinctness: = ≠
• Order: < >
• Addition: + -
• Multiplication: × /

给定上述属性，即可以定义四种不同类型的属性：

• Nominal attribute 名词属性
  • Examples: ID numbers, eye color, zip codes
  • Properties: distinctness
• Ordinal attribute 顺序属性
  • Examples: rankings (e.g., taste of potato chips on a scale from 1-10), grades, height in {tall, medium, short}
  • Properties: distinctness & order
• Interval attribute 区间属性
  • Examples: calendar dates, temperatures in Celsius or Fahrenheit.
  • Properties: distinctness, order & addition 可区分且可排序且可累加
• Ratio attribute 比率属性
  • Examples: temperature in Kelvin, length, time, counts
  • Properties: all 4 properties

1.1.2 根据取值个数划分

• Discrete Attribute 离散型属性：只有一个有限的或可数的无限值集。常表示为整数常量。
• Continuous Attribute 连续性属性：有实数作为属性值。常表示为浮点变量

1.1.3 非对称属性

Asymmetric Attributes 非对称属性。对于非对称属性，只有存在一个非零属性值被认为是重要的。

举例： 考虑一个数据集，其中每个对象是一个学生，每个属性记录一个学生是否在大学上过特定的课程。这种情况下，关注非零值是有意义的。

---

1.2 结构化数据

结构化数据的重要特征：

• 维数
  • 数据集中的对象所拥有的属性的数量
  • 具有少量维数的数据往往与中等或高维数据有质的不同
  • 维度灾难，降维
• 稀疏
  • 只存在计数
  • 对象的大多数属性的值为0，不到1%的条目是非零的
• 分辨率
  • 数据可以在不同的分辨率水平上获得，数据的特性在不同的分辨率下是不同的
  • 模式取决于分辨率的水平：
    • 太精细，模式可能看不到，也可能埋在噪音中
    • 太粗糙，模式可能消失
    • 例如，大气压力的变化
      • 小时上的变化反映了风暴和其他天气系统的运动
      • 在月尺度上，这种现象是无法检测到的

---

2. 数据集的类型

2.1 记录数据

记录数据（Record Data ）是由一组记录组成的数据，每个记录都由一组固定的属性组成。

2.1.1 数据矩阵

数据矩阵（Data Matrix）：数据对象具有相同的固定的数字属性集，因此数据对象可以被认为是多维空间中的点，其中每个维度代表一个不同的属性。

2.1.1 文档数据

文档数据（Document Data ）：每个文档都成为一个单词向量，每个单词都是该向量的一个分量（属性），每个分量的值是文档中单词出现的次数。（文本向量化操作）

2.1.3 事务数据

事务数据（Transaction Data ）：一种特殊类型的记录数据，其中每个记录（事务）涉及一组“项”。

例如，考虑一家杂货店。顾客在一次购物旅行中购买的一组产品构成一个事务，而购买的一组产品中的个别产品即是“项”。

TID	Items
1	Bread, Coke, Milk
2	Beer, Bread
3	Beer, Coke, Diaper, Milk
4	Beer, Bread, Diaper, Milk
5	Coke, Diaper, Milk

---

2.2 图数据

图数据（ Graph-Based Data ）：图有时可以是数据的方便和强大的表示。 可以用来表示数据对象之间的关系。

对象之间的关系经常传达重要信息。 在这种情况下，数据通常表示为图表。

数据对象映射到图的节点，而对象之间的关系则由对象和链接属性（如方向和权重）之间的链接来捕获。

例如：World Wide Web 万维网、Molecular Structures 分子结构

---

2.3 有序数据

有序数据（Ordered Data ）：对于这种类型的数据，属性具有涉及时间或空间顺序的关系。

2.3.1 空间坐标数据

空间坐标数据（Spatial Data ）：有些对象具有空间属性，如位置或区域，以及其他类型的属性。

例如：天气数据（降水(降水量)、温度、压力）

空间自相关：物理上接近的对象在其他方面也倾向于相似

2.3.3 顺序数据/时间数据

顺序数据/时间数据 （Sequential Data/Temporal Data）：可以被认为是记录数据的扩展，其中每个记录都有与其相关的时间。

例如，零售交易数据集存储交易发生的时间。

时间也可以与每个属性相关联。这导致了“购买DVD播放器的人倾向于在购买后立即购买DVD”的模式可以被发现

2.3.3 序列数据

序列数据（Sequence Data ）：是单个实体的序列，如单词或字母的序列。 与顺序数据非常相似，只是没有时间戳；相反，有顺序序列中的位置。

2.3.4 时间序列数据

时间序列数据（Time series data）：是一种特殊类型的顺序数据，其中每个记录都是一个时间序列，即随着时间的推移而进行的一系列测量。

时间自相关：如果两个测量值在时间上接近，那么这些测量值往往非常相似

---

3. 数据质量

数据挖掘应用程序通常应用于为另一目的收集的数据，或用于未来但未指定的应用程序。数据挖掘聚焦于：检测和纠正数据质量问题和使用容忍数据质量差的算法。

Who Define Data Quality？The person who uses the data.

A small set of data quality attributes that are commonly selected：

• Amount of the data：数据量
• Objectivity：客观性
• Availability：可用性
• Timeliness：时效性

3.1 多维度衡量

• 正确性、完整性、一致性、实时性、可信性、附加价值、可解释性、可实现性

3.2 数据质量问题

• 缺失值、不一致值、重复数据、噪声数据和异常值

质量决策必须基于质量数据，数据仓库需要对质量数据进行一致整合。

噪声是指对原始值修改后的数据

异常是特征与数据集中的大多数其他数据对象有很大的不同的数据

---

4. 数据预处理

4.1 数据清理

Data cleaning，填写缺失值，平滑噪声数据，识别或删除异常值，解决不一致

4.1.1 填充缺失值

• 减少数据集，消除所有缺失值样本
  • 只适用于该场景：如果大型数据集可用，并且只有一小部分数据缺少值
• 查找丢失数据的值
  • 领域专家检查并输入合理、可能的数据，以及缺失数据的期望值
  • 自动将缺失的值替换为一些常量
    • 将缺失的值替换为单个全局常量
    • 将缺失的值替换为其特征均值
    • 将缺失的值替换为其给定类的特征均值
    • 将缺失的值替换为最可能的值

4.1.2 识别异常值并平滑噪声数据

测量变量中的随机误差或方差，可能是伪造数据收集工具，存在数据录入问题，技术限制，数据传送问题，命名规则不一致等问题导致的。

4.1.2.1 噪声数据

• Binning：对数据进行排序并划分到回收箱，通过bin方法、bin中值或bin边界等来平滑bin中的每个数据。

  • 等宽度分割

    • 例如：

    • Sorted data: 4, 7, 9, 12, 21, 22, 29, 30, 31, 34, 37, 38

      ◼ Partition into equal-width bins:

      ◆ Bin 1 (4-14): 4, 7, 9, 12

      ◆ Bin 2 (15-25): 21, 22

      ◆ Bin 3 (26-38): 29, 30, 31, 34, 37, 38

      ◼ Smoothing by bin means:

      ◆ Bin 1: 8, 8, 8, 8

      ◆ Bin 2: 21, 21

      ◆ Bin 3: 33, 33, 33, 33, 33

      ◼ Smoothing by bin boundaries:

      ◆ Bin 1: 4, 4, 12, 12

      ◆ Bin 2: 21, 22

      ◆ Bin 3: 29, 29, 29, 38, 38,38

  • 等深度分割

    • 例如：

    • Sorted data: 4, 8, 9, 15, 21, 21, 24, 25, 26, 28, 29, 34

      ◼ Partition into equal-depth bins:

      ◆ Bin 1: 4, 8, 9, 15

      ◆ Bin 2: 21, 21, 24, 25

      ◆ Bin 3: 26, 28, 29, 34

      ◼ Smoothing by bin means:

      ◆ Bin 1: 9, 9, 9, 9

      ◆ Bin 2: 23, 23, 23, 23

      ◆ Bin 3: 29, 29, 29, 29

      ◼ Smoothing by bin boundaries:

      ◆ Bin 1: 4, 4, 4, 15

      ◆ Bin 2: 21, 21, 25, 25

      ◆ Bin 3: 26, 26, 26, 34

• 回归：通过将数据拟合为回归函数来平滑

• 聚类：检测和删除异常值

• 计算机和人为检查相结合：计算机检测可疑值后交给人检查

4.1.2.2 异常数据

删除异常数据，即删除与大多数数据不一致的数据点。例如：某人年龄属性为200的数据等等。

删除方法：聚类、使用给定模型进行假设检验、曲线拟合…

4.1.3 纠正不一致的数据

数据不一致检测方法：

• 使用元数据（例如域、范围、依赖项、分布)
• 检查由开发人员将新属性定义压缩到已定义属性的未使用部分的字段重载
• 检查唯一性规则、连续规则和空规则
  • 唯一性规则：给定属性的每个值必须与该属性的所有其他值不同
  • 连续规则：属性的最低值和最高值之间不能有缺失值，并且所有值也必须是唯一的
  • 空规则：指定使用空格、问号、特殊字符或其他表示空条件的字符串
• 使用商业工具
  • 数据擦除：使用简单的领域知识（例如邮政编码、拼写检查）来检测错误并进行更正
  • 数据审计：通过分析数据来发现规则和关系来检测违反者(例如，关联和聚类以查找异常值）

一旦我们发现差异，我们通常需要定义和应用一系列转换来纠正它们：

• 数据迁移工具：允许指定转换，例如将字符串“性别”替换为“性别”
• ETL（提取/转换/加载）工具：允许用户通过图形用户界面指定转换

4.1.4 处理重复数据

迭代和交互，两个过程的整合。 (e.g., Potter’s Wheels: http://control.cs.berkeley.edu/abc/)

---

4.2 数据集成

Data integration，多个数据库、数据立方体或文件的集成。将来自多个源的数据组合成一个连贯的存储。

多个数据库集成时，经常会出现数据冗余问题。仔细整合来自多个来源的数据可能有助于减少/避免冗余和不一致，并提高挖掘速度和质量。冗余属性可以通过相关分析来检测。

4.2.1 相关分析（数值数据）

皮尔森乘积矩相关系数：

该值大于0，表示A、B呈正相关，且值越大，其正相关性越大。

该值等于0，表示A、B相互独立。

该值小于0，表示A、B呈负相关，且值越小，其负相关性越大。

4.2.2 相关分析（类别数据）

Χ2（卡方）检验：

其中，Oij = Count(A = ai, B = bi); eij = Count(A = ai) × Count(B = bi) / N

卡方检测的值越大，变量相关性越大。

举个例子：

注意：相关性 ≠ 因果关系

---

4.3 数据转换

Data transformation，归一化和聚合

• 平滑：去除数据中的噪声
• 聚合：数据立方体构建
• 泛化：概念层次爬升
• 归一化：缩放到在一个较小的指定范围内
  • 最小-最大归一化：v’ = (v - min/max - min)(new_max - new_min) + new_min （例如：将区间[12000，98000]内的73600归一化到 0 - 1 之间：(73600 - 12000/98000 - 12000)(1 - 0) + 0 = 0.716）
  • Z 分归一化：v‘ = v - μ / σ （μ：平均值；σ：标准差）
  • 十进制缩放归一化：v’ = v / 10^j （j 是使得 |v’| 小于 1 的最大整数）
• 属性/特征构造：由给定的属性构造的新属性

---

4.4 数据缩减

Data reduction，获得体积小得多但却产生相同（或几乎相同）分析结果的数据集的简化表示。

数据缩减的策略：

• 数据聚集：将两个或多个属性（或对象)组合成单个属性(或对象）
• 数据压缩
  • 字符串压缩：运行长度编码(RLE行程编码)是一种简单的压缩形式（仅适用于存在大量重复字符的情况）
  • 音频/视频压缩：典型的有损压缩，渐进细化
• 数值缩减：通过选择替代的、较小的数据表示形式来减少数据量
  • 参数方法：假设数据适合某一模型，估计模型参数，只存储参数，并丢弃数据（可能的异常值除外）
  • 非参数方法：不假设模型。使用直方图、聚类、抽样…
• 离散化和概念层次生成
• 降维

数据缩减的方法：

• 回归：Y = w X + b
• 直方图：将数据分成桶，并存储每个桶的平均值
  • 等宽
  • 等频（等深）
  • V-optimal
  • MaxDiff： 避免将具有极大不同的源参数值的属性值放入一个桶中。 根据值之间的距离创建桶。通常比以前在大多数情况下呈现的直方图具有更好的性能
• 聚类：之后再讲
• 抽样： 获取少量样本表示整个数据集N。抽样是数据选择的主要技术，经常用于对数据的初步调查和最终的数据分析。
  • 统计学家抽样是因为获得感兴趣的整套数据太贵或太耗时。
  • 抽样用于数据挖掘，因为处理整套感兴趣的数据过于昂贵或耗时。
  • 如果样本具有代表性，那么使用一个样本几乎和使用整个数据集一样有效
  • **抽样方法：**随机抽样、有/无放回抽样、分层抽样（先分块，再从各个块进行抽样）
  • 处理不平衡数据时：上采样 / 下采样

---

4.5 数据离散

Data discretization，通过将属性的范围划分为间隔来减少给定连续属性的值数。（数值型 - > 名词型）

目的是用来减少数据大小， 且一些分类算法只接受分类属性。

离散化方法：

• 监督 & 无监督
• 自顶向下 & 自底向上（分割 & 合并）
• 具体的离散化方法：
  • 直方图分析：自顶向下、无监督
  • 聚类分析：后面讲
  • 基于熵的离散化：自顶向下、有监督（学到决策树会展开详细学习）
  • 卡方分析：有监督、自底向上
  • 自然分区分割：3-4-5 准则

概念层次生成： 通过收集和替换低级别的概念（如年龄的数值)，用更高级别的概念(如年轻人、中年人或老年人)来递归地减少数据）

---

5. 相似性和不相似性的度量

相似度： 两个数据对象有多相似的数值。数值越高，相似度越高。

不相似度：两个数据对象有多不同的数值。数值越高，相似度越低。

接近（邻近性）是指相似性或不相似性。

在实践中，属性有许多不同的类型，因此需要一个整体的相似性。 一种简单的方法是：

分别计算每个属性之间的相似性，然后使用一种导致0和1之间相似性的方法来处理这些相似性。通常，总体相似性被定义为所有个体属性相似性的平均值。

不幸的是，如果某些属性是不对称属性，这种方法就不能很好地工作。解决这个问题的最简单方法是，当两个对象的相似度计算值都为0时，从相似度计算中省略不对称属性。（ 类似的方法也能很好地处理缺失值）

5.1 欧氏距离

注意：

• 如果尺度不同，标准化是必要的
• 欧氏距离对所涉及变量的尺度极其敏感
• 欧氏距离对相关变量视而不见
• 在几何情况下，所有变量都以相同的长度单位测量
• 建模问题可能处理具有不同的尺度的变量 ，如年龄、身高、体重等。 这些变量的尺度是不可比较的

---

5.2 米科夫斯基距离

其中，r是参数，n是属性的维数：

• 当 r = 1 时，相当于曼哈顿距离、L1正则化
• 当 r = 2 时，相当于欧氏距离、L2正则化
• 当 r = ∞ 时，Lmax 正则化、L∞ 正则化

---

5.3 马氏距离

马氏距离在计算距离时考虑了变量之间的协方差

通过这种度量，欧氏距离固有的尺度和相关性问题不再是一个问题

---

5.4 距离的共性

假设d(p，q)是点 p 和 q 之间的距离，距离有如下几个特性：

• 肯定性：d(p, q) ≥0 for all p and q; and d(p, q) = 0 only if p = q.
• 对称性：d(p, q) = d(q, p) for all p and q.
• 三角不平等：d(p, r) ≤ d(p, q) + d(q, r) for all points p, q, and r.

满足这些性质的距离即为，度量。

一些补充：

余弦相似度：cos( d1, d2 ) = (d1 • d2) / ||d1 || ||d2 ||

---

5.5 相关性

相关性可以度量对象之间的线性关系，为了计算相关性，可以将数据对象p和q标准化（正态标准化），然后取它们的点积。

---

5.6 使用权重

有时，一些属性对邻近的定义比其他属性更重要。为了解决这种情况，可以通过加权每个属性的贡献来修改相关公式，例如：使用介于0到1之间的权重wk，并将其求和为1。

---

5.7 选择合适的度量方式

稠密又连续的数据，可以使用欧氏距离的方式进行度量（结合标准化和添加权重等操作）。

稀疏又离散的数据，可以使用余弦相似度、杰卡德相似度的方式进行度量。