【数据结构与算法】二叉树基础OJ -- 上 (巩固提高)

前言：

个人主页:​​​​​​Dream_Chaser～ 

✨✨刷题专栏:http://t.csdn.cn/UlvTc

⛳⛳本篇内容:力扣上二叉树OJ基础练习

​​​​​​​

目录

leetcode 965.单值二叉树

题目描述:

解题思路:

leetcode 100.相同的树

题目描述:

解题思路:

leetcode 101.对称二叉树

题目描述:

解题思路:

leetcode 144.二叉树的前序遍历(需要数组存储)

题目描述:

解题思路：

leetcode 572.另一棵树的子树

题目描述:

解题思路:

---

leetcode 965.单值二叉树

题目来源：965. 单值二叉树 - 力扣（LeetCode）

题目描述:

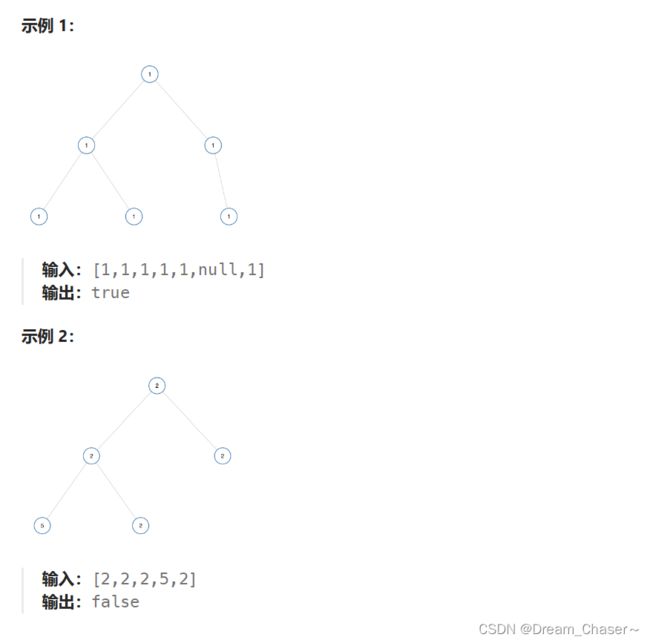
如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 :

解题思路:

        a == b b == c  推论: a == c，利用了值的传递性，根与子树也是可以利用这一性质解题。

        1.开始的时候先判断这棵树是否为空，假设是空，那么直接返回true，因为NULL也可以是这棵树唯一的一个值。

       

         2.接着若根节点不为空，那么这时候先访问根的左子树root->left，让其作为if的判断条件(判断左子树是否为空),然后用&&连接起另一个判断条件:root->left->val != root->val 也就是访问左子树的val与其根节点的val是否不相等，

        这里着重说明一下:root->val 如果等于root->left->val是说明不了问题的，因为相等了还是要找下一个节点判断与其根节点什么关系，这属于是不确定的条件,

        所以要找确定的条件:直接让root->left->val != root->val，如果条件成立则直接返回false.

右子树同理.

       

        3.如果根节点与子树相等,那么就直接让isUnivalTree(root->left) && isUnivalTree(root->right)作为返回条件.

        用&&的原因就是有其中一棵子树值不全相等,那么说明该树不是单值,返回false

图解:

代码实现:

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
        return true;
    
    if(root->left && root->left->val != root->val)
        return false;

    if(root->right && root->right->val != root->val)
        return false;

    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

执行：

leetcode 100.相同的树

题目来源:100. 相同的树 - 力扣（LeetCode）

题目描述:

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例:

解题思路:

1. 首先检查两棵树是否都为空。如果是，则它们具有相同的值，返回true。
2. 如果两棵树中有一棵为空而另一棵不为空，则它们不相等，返回false。
3. 如果两棵树的当前节点的值不相等，则它们不相等，返回false。
4. 如果以上情况都不满足，即两棵树的当前节点的值相等，则递归地调用isSameTree函数，传入左子树，并进行相同的比较。
5. 同样地，递归地调用isSameTree函数，传入右子树，并进行相同的比较。
6. 如果左右子树的比较结果都为true，则说明两棵树相等，返回true；否则返回false

图解:图上数字代表遍历顺序，说明两子树是同时进行的。

 代码实现:

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    //找确定的条件
    //两树皆为空时，它们具有相同的值 
    if(p == NULL && q == NULL)
        return true;
    //当两树一个节点为空，另一个不为空
    if(p == NULL || q == NULL)
        return false;
    //都不为空，但是不相等，
    if(p->val !=q->val)
        return false;
    
    //假设两树第一个节点相等,则递归函数,反复上述过程
    return isSameTree(p->left,q->left) 
    && isSameTree(p->right,q->right);
}

执行:

leetcode 101.对称二叉树

题目来源:101. 对称二叉树 - 力扣（LeetCode）

题目描述:

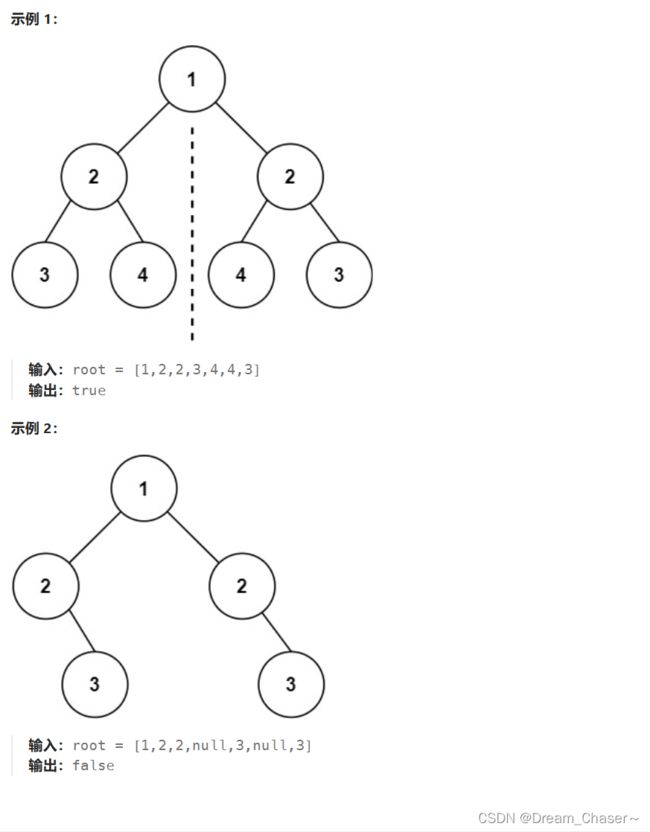
给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例:

解题思路:

         首先，因为oj里面的原函数满足不了我们在一颗树内同时操作左右子树的需求，因为只有一个指针，操作不了左右两个方向。(记住原函数包括函数名、返回条件、参数都是不能改变的)

        这时候我们定义一个函数is_Symmetrict（root->left,root->right）,接着传入指针，然后可以同时开始操作,左右子树。

        1.先判断左右子树是否为空，因为地址为空在结构上也是对称的一个结果，然后返回true

        2. 判断以下子树一个为空，另一个是否也为空，两者同时为空则返回false，

        3、两子树不为空但不相等，返回false。

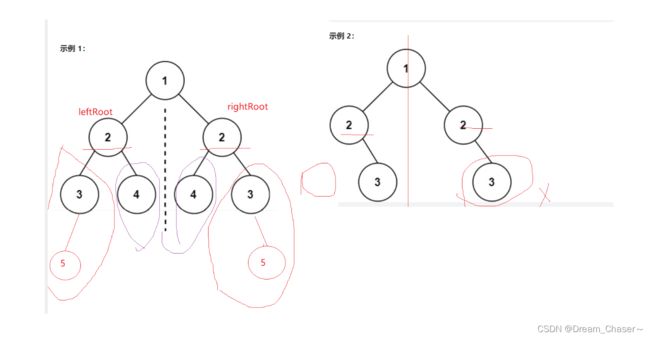
        若上述条件均不满足，即左子树和右子树都不为空，且它们的根节点的值相等，那么继续递归地调用 is_Symmetrict 函数，分别传入左子树的左子树和右子树的右子树，以及左子树的右子树和右子树的左子树。

        如果递归调用的返回值都为 true，则说明左子树和右子树对称，返回 true；否则返回 false

图解:​​​​​​​

代码实现:

bool is_Symmetrict(struct TreeNode*leftroot,struct TreeNode*rightroot)
{
    //找确定的条件
    //左子树右子树两个为空
    if(leftroot==NULL && rightroot == NULL)
        return true;

    //左子树或右子树，一个为空
    if(leftroot == NULL || rightroot == NULL)
        return false;

    if(leftroot->val != rightroot->val)
    return false;

    return is_Symmetrict(leftroot->left , rightroot->right) && 
    is_Symmetrict(leftroot->right , rightroot->left);
}
bool isSymmetric(struct TreeNode* root){
   return is_Symmetrict(root->left,root->right);   
}

执行：

leetcode 144.二叉树的前序遍历(需要数组存储)

题目来源:144. 二叉树的前序遍历 - 力扣（LeetCode）

题目描述:

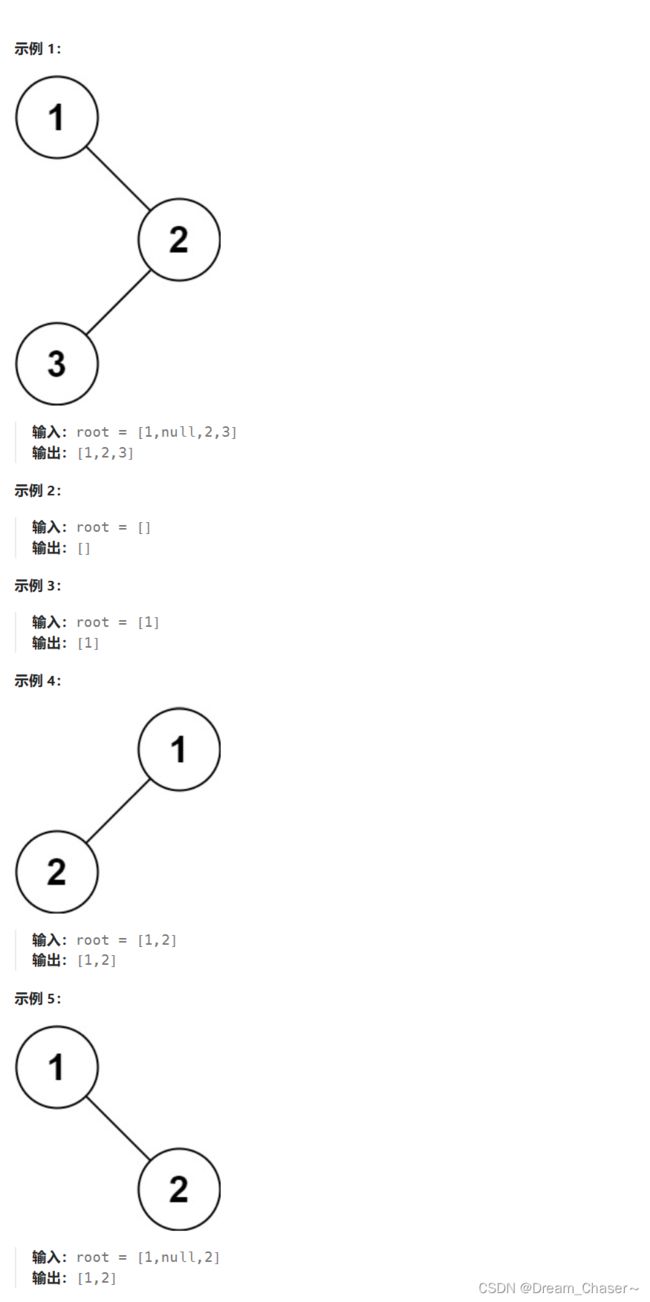
给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例:

 解题思路：

        首先用TreeSize函数算出二叉树的节点数量,具体实现看这篇文章：http://t.csdnimg.cn/DvuEU

       接着用*returnsize这个值接收，为什么要解引用?因为传过来的是size的地址-->&size

图解在这：实现其main函数:

         接着malloc一块空间，定义指针int*a指向，定义变量i，接着传入preorder函数,进行前序遍历，之后返回a的地址。

代码实现：

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0:TreeSize(root->left) + TreeSize(root->right)+1; 
}
void preorder(struct TreeNode*root,int*a,int*i)
{
    if(root==NULL)
    {
        return ;
    }
    a[(*i)++]=root->val;
    preorder(root->left,a,i);
    preorder(root->right,a,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    *returnSize = TreeSize(root);
    int* a= malloc(*returnSize*sizeof(struct TreeNode));

    int i=0;
    preorder(root,a,&i);
    return a;
}

执行：

关于此题有两个疑问:

        1.用局部变量，下面的这个代码可以吗?

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0:TreeSize(root->left) + TreeSize(root->right)+1; 
}
void _preorder(struct TreeNode* root, int* a,int i)
{
	if (root == NULL)
		return;
	//用指针的方式是为了不在不同栈帧内创建i
	a[i++] = root->val;
	_preorder(root->left, a,i);
	_preorder(root->right, a,i);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
	*returnSize = TreeSize(root);
	int* a = (int*)malloc(*returnSize * sizeof(int));

	int i = 0;
	_preorder(root,a,i);
	return a;
}

结果是不行，为什么?用局部变量就不行吗？ 

以下是我的理解: 

 2.全局变量可以吗？

        可以，但是先列举问题:

解析：        

        虽然全局变量 i 在定义时已经被初始化为 0，但是全局变量的赋值操作只会在程序启动时执行一次。每次调用 _preorder 函数时，由于没有显式地给 i 赋新的值，i 的值会保持上一次调用结束时的值。这样会导致多次调用 _preorder 函数时，节点值被存储在错误的位置，结果可能不符合预期。

        因此，在函数内部显式地给 i 赋值为 0，可以确保每次调用 _preorder 函数时都从数组 a 的开头位置开始存储节点的值，避免出现错误的索引位置。

leetcode 572.另一棵树的子树

题目来源：572. 另一棵树的子树 - 力扣（LeetCode）

题目描述:

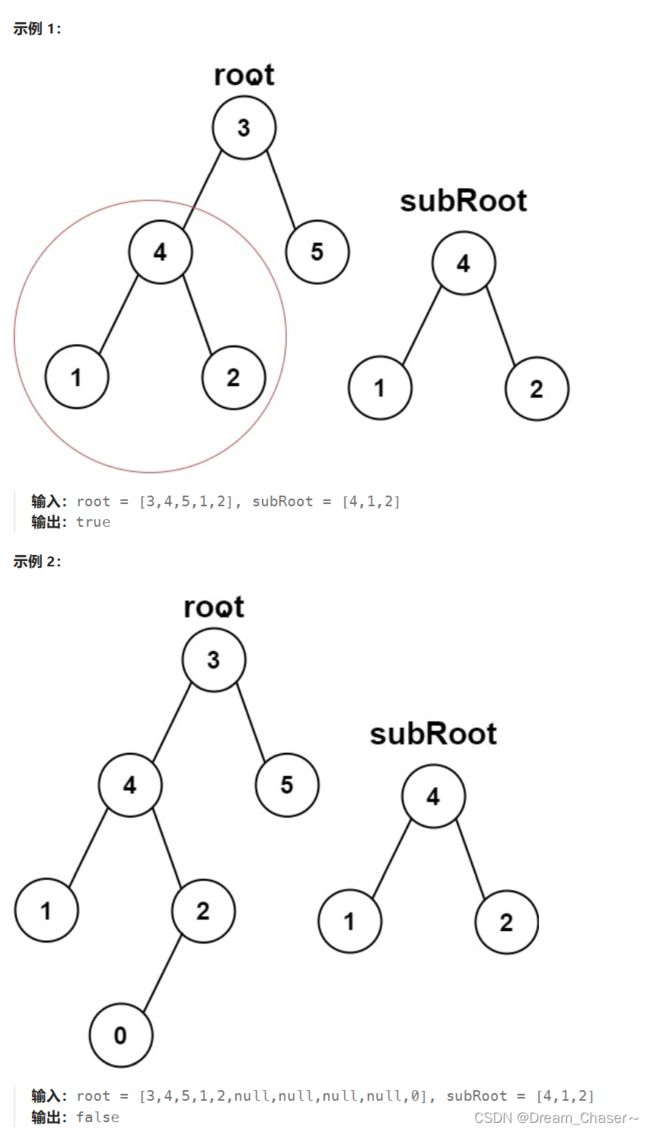
        给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

        二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例:

解题思路:

1. 首先，判断 root 是否为 NULL，如果是，则不存在子树，返回 false。
2. 接着，调用 isSameTree 函数，判断 root 和 subRoot 是否相同，如果是，则 subRoot 是 root 的子树，返回 true。
3. 如果以上条件都不满足，递归调用 isSubtree 函数，分别判断 subRoot 是否是 root 的左子树的子树，或者是 root 的右子树的子树。只要有一边存在子树，就返回 true。
4. 如果都不满足，则 subRoot 不是 root 的子树，返回 false。

图解：

代码实现:

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    //找确定的条件
    if(p == NULL && q == NULL)
        return true;
    
    if(p == NULL || q == NULL)
        return false;

    if(p->val !=q->val)
        return false;
   
    return isSameTree(p->left,q->left) 
    && isSameTree(p->right,q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    
    if(root==NULL)
    {
        return false;
    }
    if(isSameTree(root,subRoot))
    {
        return true;
    }
    return isSubtree(root->left,subRoot) 
    || isSubtree(root->right,subRoot);
}

代码执行:
​​​​​​​

        本篇文章在这里就结束了，如有需要补充的，欢迎评论！