数据结构第二章线性表顺序表练习题及答案P19

数据结构第二章线性表顺序表练习题及答案P19

1、从顺序表中删除具有最小值的元素(假设唯一)并由函数返回被删元素的值。

空出的位置由最后一个元素填补，若顺序表为空则显示出错信息并退出运行

算法思想：搜索整个顺序表，查找最小值元素并记住其位置，搜索结束后用最后一个元素填补空出的原最小值元素的位置

bool Del_Min(SeqList &L,ElemType &value){
	if(L.length<=0) return false; 
	int pos=0;
	value=L.data[0];
	for(int i=1;i

---

2、设计一个高效算法，将顺序表L的所有元素逆置，要求算法的空间复杂度为O（1）

算法思想：扫描顺序表L的前半部分元素，对于元素L.data[i] (0

bool Reverse(SeqList &L){
	ElemType temp;
	for(int i=0;i

---

3、对长度为n的顺序表L，编写一个时间复杂度为O(n)、空间复杂度为O(1)的算法，该算法删除线性表中所有值为x的数据元素

算法思想1：用k记录顺序表L中不等于x的元素个数(即需要保存的元素个数),边扫描L边统计k,并将不等于x的元素向前移动k个位置，最后修改L的长度。

void del_x_1(SeqList &L,ElemType x){
	int k=0;
	for(int i=0;i

---

算法思想2：用k记录顺序L中等于x的元素的个数，边扫描L边统计k,并将不等于x的元素前移k个位置,最后修改L的长度

void del_x_2(SeqList &L,ElemType x){
	int k=0,i=0;                       //k记录值等于x的元素个数 
	while(i

---

4、从有序顺序表中删除其值在给定值s与t之间(要求s < t)的所有元素，如果s或t不合理或顺序表为空，则显示出错信息并退出运行

算法思想：先寻找值大于等于s的第一个元素(第一个删除的元素),然后寻找值大于t的第一个元素(最后一个删除的元素的下一个元素),
要将这段元素删除，只需直接将后面的元素前移

bool Del_s_t2(SqList &L,ElemType s,ElemType t){
	int i,j;
	if(s>=t || L.length==0) return false;
	for(i=0;i=L.length) return false;				  //所有元素值均小于s，返回 
	for(j=i;j

---

5、从顺序表中删除其值在给定值s与t之间(要求s < t)的所有元素，如果s或t不合理或顺序表为空，则显示出错信息并退出运行

算法思想：从前向后扫描顺序表L，用k记录下元素值在s到t之间元素的个数(初始时k=0).对于当前扫描的元素，若其值不在s到t之间，则前移k个位置：否则执行k++。由于这样每个不再s到t之间的元素仅移动一次，所以算法效率高

bool Del_s_t(SqList &L,ElemType s,ElemType t){
	int k,i;
	if(s>=t || L.length==0) return false;
	for(i=0,k=0;i=s && L.data[i]<=t){
			k++;
		}else{
			L.data[i-k]=L.data[i];
		}
	}       
	L.length=L.length-k;
	return true;
}

---

6、从有序顺序表中删除所有其值重复的元素，使表中所有元素的值均不同

算法思想：注意是有序顺序表，值相同的元素一定在连续的位置上，用类似于直接插入排序的思想，初始时将第一个元素视为非重复的有序表。
之后依次判断后面的元素是否与前面非重复有序表的最后一个元素相同，若相同则继续向后判断，若不同则插入到前面的非重复有序表的最后，直至判断到表尾为止

bool Delete_Same(SeqList &L){
	int i=0,j;
	for(j=1;i

---

7、将两个有序顺序表合并为一个新的有序顺序表，并由函数返回结果顺序表

算法思想：首先，按顺序不断取下两个顺序表表头较小的结点存入新的顺序表中。
然后，看哪个表还有剩余，将剩下的部分加到新的顺序表后面

bool Merge(SqList A,SqList B,SqList C){
	if(A.length+B.length>C.maxSize){
		return false;
	}
	int i=0,j=0,k=0;
	while(i

---

8、(重点)已知在一维数组A[m+n]中依次存放两个线性表(a1,a2,a3,…,am)和(b1,b2,b3,…,bn).

试编写一个函数，将数组中两个顺序表的位置互换，即将(b1,b2,b3,…,bn)放在(a1,a2,a3,…,am)的前面。

算法思想：先将数组A[m+n]中全部元素(a1,a2,a3,…,am,b1,b2,b3,…,bn)原地逆置为 (bn,…,b3,b2,b1,am,…,a3,a2,a1),
再对前n个元素和后m个元素分别使用逆置算法，即可得到(b1,b2,b3,…,bn,a1,a2,a3,…,am),从而实现顺序表的位置互换。

typedef int DataType;
void Reverse(DataType A[],int left,int right,int arraySize){
	//逆转(aleft,aleft+1,aleft+2...,aright)为(aright,aright-1,...,aleft)
	if(left>=right || right>=arraySize) return;
	int mid=(left+right)/2;
	for(ing i=0;i<=mid-left;i++){
		DataType temp=A[left+i];
		A[left+i]=A[right-i];
		A[right-i]=temp;
	}
} 
void Exchange(DataType A[],int m,int n,int arraySize){
	/*数组A[m+n]中，从0到m-1存放顺序表(a1,a2,a3,...,am)，
	从m到m+n-1存放顺序表 (b1,b2,b3,...,bn)，算法将这两个表的位置互换*/
	Reverse(A,0,m+n-1,arraySize);
 	Reverse(A,0,n-1,arraySize);
 	Reverse(A,n,m+n-1,arraySize);
}

---

9、线性表 (a1,a2,a3,…,an)中元素递增有序且按顺序存储于计算机内。要求设计一算法，完成用最少时间在表中查找数值为x的元素，若找到则将其与后继元素位置相交换，若找不到则将其插入表中元素仍递增有序

算法思想：顺序存储的线性表递增有序，可以顺序查找，也可以折半查找。
题目要求“用最少的时间在表中查找数值为x的元素”，这里应使用折半查找法

void SearchExchangeInsert(ElemType A[],ElemType x){
	int low=0,high=n-1,mid;                   //low和high指向顺序表下界和上界的下标 
	while(low<=high){			              
		mid=(low+high)/2;                     //找中间位置 
		if(A[mid]==x) break;                  //找到x，退出while循环 
		else if(A[mid]high){                            //查找失败，插入数据元素x 
		for(i=n-1;i>high;i--) A[i+1]=A[i];   //后移元素 
		A[i+1]=x;                            //插入x 
	}
} 

---

10、【2010统考真题】设将n(n>1)个整数存放到一维数组R中。设计一个在时间和空间两方面都尽可能高效的算法。将尺中保存的序列循环左移p(0 < p < n)个位置，即将R中的数据由

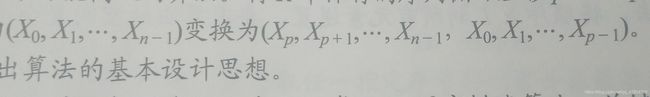
要求：
1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++或Java语言描述算法，关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。

10.2
void Reverse(int R[],int from,int to){
	int i,temp;
	for(i=0;i<(to-from+1)/2;i++){
		temp=R[from+i];
		R[from+i]=R[to-i];
		R[to-i]=temp;
	}
} 
void Converse(int R[],int n,int p){
	Reverse(0,p-1)                //得到cbadefgh
	Reverse(p,n-1)                //得到cbahgfed
	Reverse(0,n-1)                //得到defghabc
}

10.3 上诉算法中三个Reverse函数的时间复杂度分别为O(p/2)、O((n-p)/2)、O(n/2),
故所设计的算法的时间复杂度为O(n),空间复杂度为O(1).

---

11、【2011统考真题】一个长度为L(L>1)的升序序列S,处在第「L/2个位置的数称为S的中位数。例如，若序列S1=(11,13,15,17,19),则S1的中位数是15,两个序列的中位数是含它们所有元素的升序序列的中位数。例如，若S2=(2,4,6,8,20),则S1和S2的中位数是11.现在有两个等长升序序列A和B,试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数。要求：

1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++或Java语言描述算法，关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。

11.2
int M_search(int A[],int B[],int n){
int s1=0,d1=n-1,m1,s2=0,d2=n-1,m2;   //分别表示序列A和B首位数、末位数、中位数
while(s1!=d1 || s2!=d2){
	m1=(s1+d1)/2;
	m2=(s2+d2)/2;
	if(A[m1]==B[m2])
		return A[m1];                //满足条件1 
	if(A[m1]

---

12、【2013统考真题】已知一个整数序列A=(ao,a1,…,an-1),其中0≤a; < n(0 ≤ i < n).若存在ap1=an2=···=apm=x且m>n/2(0 ≤ pk < n,1≤k≤m),则称x为A的主元素。例如A=(0,5,5,3,5,7,5,5),则5为主元素；又如A=(0,5,5,3,5,1,5,7),则A中没有主元素。假设A中的n个元素保存在一个一维数组中，请设计一个尽可能高效的算法，找出A的主元素。若存在主元素，则输出该元素；否则输出－1.要求：

1)给出算法的基本设计思想。
2)根据设计思想，采用C或C或Java语言描述算法，关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。

12.2
int Majority(int A[],int n){
int i,c,count=1;               //c用来保存候选主元素，count用来计数 
c=A[0];                        //设置A[0]为候选主元素
for(i=1;i0){      	   //处理不是候选主元素的情况 
			count--;
		} 
		else{                  //更换候选主元素，重新计数 
			c=A[i];
			count=1;
		}
	}
} 
if(count>0){
	for(i=count=0;in/2) return c;   		//确认候选主元素 
else return -1;                 //不存在主元素 
} 

12.3 实现的程序的时间复杂度为O(n),空间复杂度为O(1).
说明：本题如果采用先排好序再统计的方法【时间复杂度可为O(nlog2n)】,只要解答正确，最高可拿11分。
即便是写出O(n2方)的算法，最高也能拿10分，因此对于统考算法题，花费大量时间去思考最优解是得不偿失的

---

13、【2018统考真题】给定一个含n(n>1)个整数的数组，请设计一个在时间上尽可能高效的算法，找出数组中未出现的最小正整数。例如，数组｛－5,3,2,3}中未出现的最小正整数是1;数组｛1,2,3}中未出现的最小正整数是4.要求：

1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。

13.2
int findMissMin(int A[],int n){
int i,*B;                          //标记数组 
B=(int*)malloc(sizeof(int)*n);     //分配空间 
memset(B,0,sizeof(int)*n);         //赋初始值为0 
for(i=0;i0 && A[i]<=n){         //若A[i]的值介于1~n,则标记数组B 
 		B[A[i]-1]=1;
 	}
 }
for(i=0;i

---