人工智能AI 全栈体系(十)
第一章 神经网络是如何实现的
到目前介绍的循环神经网络中,每个子网络还比较简单,存在不少问题。比如当句子比较长时,也存在类似梯度消失的问题,只是这种梯度消失不是沿着纵向发生的,而是沿着横向产生。
横向产生是什么意思呢?
以句子情感分类为例说明。这种方法其实是先将句子编码为一个向量,再利用该向量进行情感分类。这样在用BP算法求解时,梯度是从最后的输出反传到句子的最后一个词,再到倒数第二个词……,这样一个词一个词地最后传到第一个词。这样的反传过程中,和层数比较多的神经网络一样,可能会造成梯度消失问题。
九、长短期记忆网络(LSTM:Long Short-Term Memory)
- 除了梯度消失问题外,还有其他问题。对不同的任务,一句话中不同的词所起的作用是不一样的。比如对于情感分类问题,“我非常喜欢看这部城市题材电影”这句话中,“非常”、“喜欢”的作用就比较大,“这部”作用就比较小,“城市”、“题材”也有些作用,但远没有“喜欢”的作用大。但是如果是对于内容分类任务来说,“看”、“电影”的作用可能就比较大,而“喜欢”可能作用就小得多。所以对于相同的一句话,对于不同的任务,句中每个词的作用是不一样的,在网络中应该尽可能体现出这种不同。

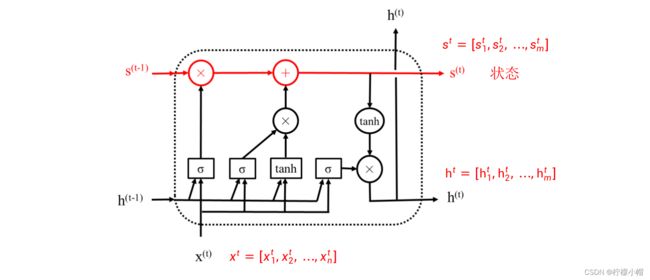
- 为了解决普通循环神经网络存在的这种不足,研究者提出了改进方案,长短期记忆网络就是其中的一种。下图给出了一个长短期记忆网络模块示意图,简称为LSTM(Long Short-Term Memory),该模块相当于普通循环神经网络中的子网络。
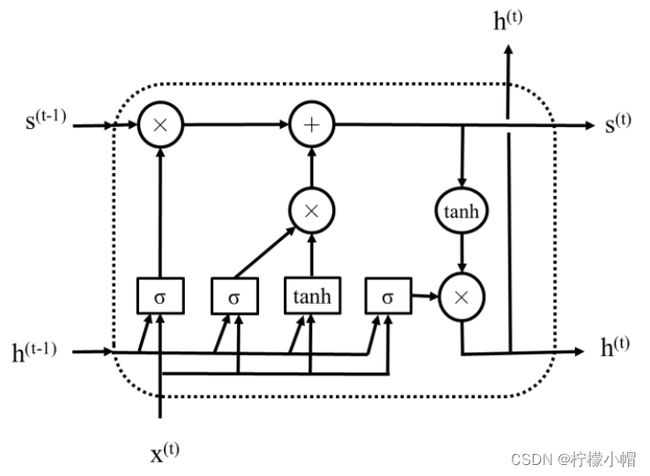
- 在LSTM中,最主要的是引入了遗忘门、输入门和输出门3个门。
1. “门”的概念
- 所谓“门”其实就是一个只有输入层和输出层的神经网络,输出层连接sigmoid激活函数,每个神经元的输出为0、1之间的一个值,用于对某些信息进行选择。如图(a)给出了一个门的示意图,图(b)是它的简化图,其中虚线框部分就是一个“门”,输入为 x = [ x 1 , x 2 , . . . , x n ] x = [x_1, x_2, ... , x_n] x=[x1,x2,...,xn] ,输出为 g = [ g 1 , g 2 , . . . , g m ] g = [g_1, g_2, ... , g_m] g=[g1,g2,...,gm] ,由于在输出层使用了sigmoid激活函数,所以输出层的每个神经元的输出值 g i g_i gi 都满足 0 ≤ g i ≤ 1 0 \leq g_i \leq 1 0≤gi≤1。门是一种可选地让信息通过的方式,如果用 g i g_i gi 去乘以某个量,则实现了对该量有选择地通过的目的。当 g i = 1 g_i = 1 gi=1 时,则该量全部通过, g i = 0 g_i = 0 gi=0 时,则该量被阻挡,而当 g i g_i gi 介于0和1之间时,则该量部分通过,这也是“门”名称的由来。图(a)中最上边 s = [ s 1 , s 2 , . . . , s m ] s = [s_1, s_2, ... , s_m] s=[s1,s2,...,sm] 就是被门控制的向量,其每个元素 s i s_i si 与 g i g_i gi 相乘(图中“⊗”表示相乘),根据 g i g_i gi 的大小对 s i s_i si 进行选择,选择后的结果形成向量 s ′ = [ s 1 ′ , s 2 ′ , . . . , s m ′ ] s' = [s'_1, s_2', ... , s_m'] s′=[s1′,s2′,...,sm′] 。
2. LSTM 模块
- 再回过头来看上图所示的LSTM模块,图中 h ( t ) = [ h 1 ( t ) , h 2 ( t ) , . . . , h m ( t ) ] h^{(t)} = [h_1^{(t)}, h_2^{(t)}, ... , h_m^{(t)}] h(t)=[h1(t),h2(t),...,hm(t)] 是模块的输出,与普通循环神经网络中的 h ( t ) h^{(t)} h(t) 含义是一样的。与普通循环神经网络不同的是多了一个表示状态的向量 s ( t ) = [ s 1 ( t ) , s 2 ( t ) , . . . , s m ( t ) ] s^{(t)} = [s_1^{(t)}, s_2^{(t)}, ... , s_m^{(t)}] s(t)=[s1(t),s2(t),...,sm(t)] ,如上图红色部分所示。引入状态是为了信息在横向连接的各模块中畅通,其作用是防止信息被淹没和梯度消失现象。但是状态并不是直接传递到下一个模块的,而是经过了一个被称作遗忘门的选择(图中红色部分的“⊗”)以及添加了与当前输入有关的信息后(图中红色部分的“⊕”)再传递到下一个模块,其作用就是有选择地对之前的状态信息加以利用,并同时叠加上当前输入的信息。
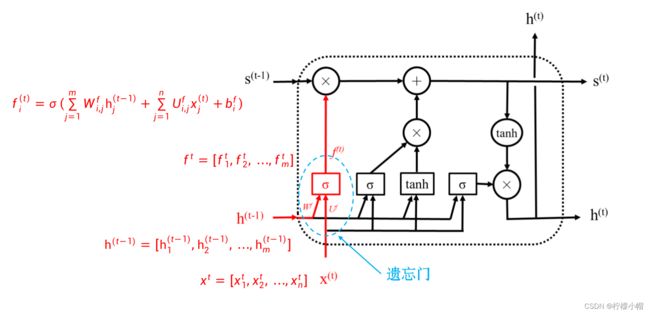
2.1 遗忘门
- 上图中的红色部分就是LSTM的遗忘门,输入是前一个模块的输出 h ( t − 1 ) = [ h 1 ( t − 1 ) , h 2 ( t − 1 ) , . . . , h m ( t − 1 ) ] h^{(t-1)} = [h_1^{(t-1)}, h_2^{(t-1)}, ... , h_m^{(t-1)}] h(t−1)=[h1(t−1),h2(t−1),...,hm(t−1)] 与当前输入 x ( t ) = [ x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) ] x^{(t)} = [x_1^{(t)}, x_2^{(t)}, ... , x_n^{(t)}] x(t)=[x1(t),x2(t),...,xn(t)] 的拼接,输出是 f ( t ) = [ f 1 ( t ) , f 2 ( t ) , . . . , f m ( t ) ] f^{(t)} = [f_1^{(t)}, f_2^{(t)}, ... , f_m^{(t)}] f(t)=[f1(t),f2(t),...,fm(t)] 。如同前面介绍过的,遗忘门就是一个典型的只有输入层和输出层的全连接神经网络,只是输入由 x ( t ) x^{(t)} x(t) 和 h ( t − 1 ) h^{(t-1)} h(t−1) 两部分组成,相当于两个向量拼接成一个长度为n+m的向量共同组成输入。下图给出了遗忘门的示意图。
-
遗忘门的具体计算如下:
f i ( t ) = σ ( ∑ j = 1 m W i , j f h j ( t − 1 ) + ∑ j = 1 n U i , j f x j ( t ) + b i f ) f_i^{(t)} = \sigma(\sum^m_{j=1}W^f_{i,j}h^{(t-1)}_j + \sum^n_{j=1}U^f_{i,j}x^{(t)}_j + b^f_i) fi(t)=σ(j=1∑mWi,jfhj(t−1)+j=1∑nUi,jfxj(t)+bif) -
其中 W i , j f ( i = 1 , . . . , m ; j = 1 , . . . m ) W^f_{i,j}(i = 1, ... , m; j = 1, ... m) Wi,jf(i=1,...,m;j=1,...m) 为前一个模块的输出第j个分量 h j ( t − 1 ) h^{(t-1)}_j hj(t−1) 到遗忘门输出层第i个神经元的连接权重, U i , j f ( i = 1 , . . . , m ; j = 1 , . . . n ) U^f_{i,j}(i = 1, ... , m; j = 1, ... n) Ui,jf(i=1,...,m;j=1,...n) 为当前输入第j个分量 x j ( t ) x^{(t)}_j xj(t) 到遗忘门输出层第i个神经元的连接权重, b i f ( i = 1 , . . . , m ) b^{f}_i(i=1,...,m) bif(i=1,...,m) 为遗忘门输出层第i个神经元的偏置, σ \sigma σ 为sigmoid激活函数。
-
遗忘门的作用是对前一个状态 s ( t − 1 ) s^{(t-1)} s(t−1) 进行选择,重要的信息选择通过,非重要的信息选择不通过,也就是“遗忘”,所以叫遗忘门。 s ( t − 1 ) s^{(t-1)} s(t−1) 经选择后再加上当前输入信息有关的内容,成为该模块的状态输出 s ( t ) s^{(t)} s(t) 。
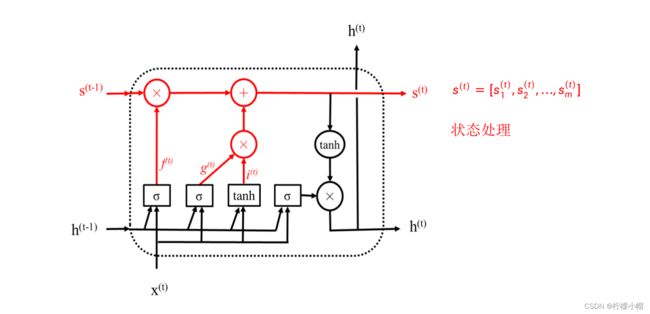
2.2 输入门
- LSTM模块的第二个门是输入门,是对当前输入信息进行选择,如上图所示。输入门的结构与遗忘门基本是一样的,其输入也是前一个模块的输出 h ( t − 1 ) = [ h 1 ( t − 1 ) , h 2 ( t − 1 ) , . . . , h m ( t − 1 ) ] h^{(t-1)} = [h_1^{(t-1)}, h_2^{(t-1)}, ... , h_m^{(t-1)}] h(t−1)=[h1(t−1),h2(t−1),...,hm(t−1)] 与当前输入 x ( t ) = [ x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) ] x^{(t)} = [x_1^{(t)}, x_2^{(t)}, ... , x_n^{(t)}] x(t)=[x1(t),x2(t),...,xn(t)] 的拼接,输出是 g ( t ) = [ g 1 ( t ) , g 2 ( t ) , . . . , g m ( t ) ] g^{(t)} = [g_1^{(t)}, g_2^{(t)}, ... , g_m^{(t)}] g(t)=[g1(t),g2(t),...,gm(t)] 。输入门的具体计算如下:
g i ( t ) = σ ( ∑ j = 1 m W i , j g h j ( t − 1 ) + ∑ j = 1 n U i , j g x j ( t ) + b i g ) g_i^{(t)} = \sigma(\sum^m_{j=1}W^g_{i,j}h^{(t-1)}_j + \sum^n_{j=1}U^g_{i,j}x^{(t)}_j + b^g_i) gi(t)=σ(j=1∑mWi,jghj(t−1)+j=1∑nUi,jgxj(t)+big)
-
其中 W i , j g ( i = 1 , . . . , m ; j = 1 , . . . m ) W^g_{i,j}(i = 1, ... , m; j = 1, ... m) Wi,jg(i=1,...,m;j=1,...m) 为前一个模块的输出第j个分量 h j ( t − 1 ) h^{(t-1)}_j hj(t−1) 到输入门输出层第i个神经元的连接权重, U i , j g ( i = 1 , . . . , m ; j = 1 , . . . n ) U^g_{i,j}(i = 1, ... , m; j = 1, ... n) Ui,jg(i=1,...,m;j=1,...n) 为当前输入第j个分量 x j ( t ) x^{(t)}_j xj(t) 到输入门输出层第i个神经元的连接权重, b i g ( i = 1 , . . . , m ) b^{g}_i(i=1,...,m) big(i=1,...,m) 为输入门输出层第i个神经元的偏置, σ \sigma σ 为sigmoid激活函数。

-
输入门控制的是输入相关的信息,LSTM是如何处理输入相关的信息呢?
-
上图给出了LSTM处理输入信息的示意图,为了表述方便我们称为输入处理单元。从图中可以看出,输入处理单元与输入门也基本一样,只是输出的激活函数换成了双曲正切(tanh),输入也是前一个模块的输出 h ( t − 1 ) = [ h 1 ( t − 1 ) , h 2 ( t − 1 ) , . . . , h m ( t − 1 ) ] h^{(t-1)} = [h_1^{(t-1)}, h_2^{(t-1)}, ... , h_m^{(t-1)}] h(t−1)=[h1(t−1),h2(t−1),...,hm(t−1)] 与当前输入 x ( t ) = [ x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) ] x^{(t)} = [x_1^{(t)}, x_2^{(t)}, ... , x_n^{(t)}] x(t)=[x1(t),x2(t),...,xn(t)] 的拼接,输出是 i ( t ) = [ i 1 ( t ) , i 2 ( t ) , . . . , i m ( t ) ] i^{(t)} = [i_1^{(t)}, i_2^{(t)}, ... , i_m^{(t)}] i(t)=[i1(t),i2(t),...,im(t)] 。这里的 i ( t ) i^{(t)} i(t) 就是对输入信息处理的结果,每一维 i i ( t ) i_i^{(t)} ii(t) 是一个正负1之间的数值,然后用输入门与其按位相乘,实现对输入信息的选择。具体计算如下:
i k ( t ) = t a n h ( ∑ j = 1 m W k , j i h j ( t − 1 ) + ∑ j = 1 n U k , j i x j ( t ) + b k i ) i_k^{(t)} = tanh(\sum^m_{j=1}W^i_{k,j}h^{(t-1)}_j + \sum^n_{j=1}U^i_{k,j}x^{(t)}_j + b^i_k) ik(t)=tanh(j=1∑mWk,jihj(t−1)+j=1∑nUk,jixj(t)+bki) -
其中 W k , j i ( k = 1 , . . . , m ; j = 1 , . . . m ) W^i_{k,j}(k = 1, ... , m; j = 1, ... m) Wk,ji(k=1,...,m;j=1,...m) 为前一个模块的输出第j个分量 h j ( t − 1 ) h_j^{(t-1)} hj(t−1) 到输入处理单元输出层第k个神经元的连接权重, U k , j i ( k = 1 , . . . , m ; j = 1 , . . . n ) U^i_{k,j}(k = 1, ... , m; j = 1, ... n) Uk,ji(k=1,...,m;j=1,...n) 为当前输入第j个分量 x j ( t ) x_j^{(t)} xj(t) 到输入处理单元输出层第k个神经元的连接权重, b k i ( l = 1 , . . . , m ) b^{i}_k(l=1,...,m) bki(l=1,...,m) 为输入处理单元输出层第k个神经元的偏置,激活函数为tanh激活函数。
- 有了遗忘门和输入门之后,就可以获得新的状态信息了,上图给出了示意图。简单说就是用遗忘门对前一个状态 s ( t − 1 ) s^{(t-1)} s(t−1) 进行选择,用输入门对当前输入相关信息 i ( t ) i^{(t)} i(t) 进行选择,然后二者相加得到新的状态 s ( t ) = [ s 1 ( t ) , s 2 ( t ) , . . . , s m ( t ) ] s^{(t)} = [s_1^{(t)}, s_2^{(t)}, ... , s_m^{(t)}] s(t)=[s1(t),s2(t),...,sm(t)] 。具体计算方法如下:
s j ( t ) = f j ( t ) × s j ( t − 1 ) + g j ( t ) × i j ( t ) s^{(t)}_j = f^{(t)}_j \times s_j^{(t-1)} + g_j^{(t)} \times i_j^{(t)} sj(t)=fj(t)×sj(t−1)+gj(t)×ij(t)
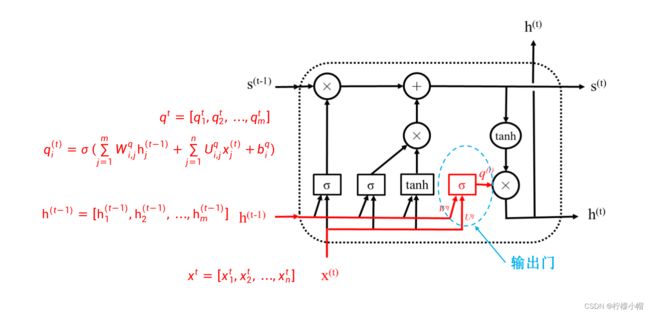
2.3 输出门
-
LSTM模块的第三个门是输出门,顾名思义是对模块的输出信息进行选择,如上图所示。输出门的结构同遗忘门基本也是一样的,其输入是前一个模块的输出 h ( t − 1 ) = [ h 1 ( t − 1 ) , h 2 ( t − 1 ) , . . . , h m ( t − 1 ) ] h^{(t-1)} = [h_1^{(t-1)}, h_2^{(t-1)}, ... , h_m^{(t-1)}] h(t−1)=[h1(t−1),h2(t−1),...,hm(t−1)] 与当前输入 x ( t ) = [ x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) ] x^{(t)} = [x_1^{(t)}, x_2^{(t)}, ... , x_n^{(t)}] x(t)=[x1(t),x2(t),...,xn(t)] 的拼接,输出是 q ( t ) = [ q 1 ( t ) , q 2 ( t ) , . . . , q m ( t ) ] q^{(t)} = [q_1^{(t)}, q_2^{(t)}, ... , q_m^{(t)}] q(t)=[q1(t),q2(t),...,qm(t)] 。输入门的具体计算如下:
q i ( t ) = σ ( ∑ j = 1 m W i , j q h j ( t − 1 ) + ∑ j = 1 n U i , j q x j ( t ) + b i q ) q_i^{(t)} = \sigma(\sum^m_{j=1}W^q_{i,j}h^{(t-1)}_j + \sum^n_{j=1}U^q_{i,j}x^{(t)}_j + b^q_i) qi(t)=σ(j=1∑mWi,jqhj(t−1)+j=1∑nUi,jqxj(t)+biq) -
其中 W i , j q ( i = 1 , . . . , m ; j = 1 , . . . m ) W^q_{i,j}(i = 1, ... , m; j = 1, ... m) Wi,jq(i=1,...,m;j=1,...m) 为前一个模块的输出第j个分量 h j ( t − 1 ) h^{(t-1)}_j hj(t−1) 到输入门输出层第i个神经元的连接权重, U i , j q ( i = 1 , . . . , m ; j = 1 , . . . n ) U^q_{i,j}(i = 1, ... , m; j = 1, ... n) Ui,jq(i=1,...,m;j=1,...n) 为当前输入第j个分量 x j ( t ) x^{(t)}_j xj(t) 到输入门输出层第i个神经元的连接权重, b i g ( i = 1 , . . . , m ) b^{g}_i(i=1,...,m) big(i=1,...,m) 为输入门输出层第i个神经元的偏置, σ \sigma σ 为sigmoid激活函数。
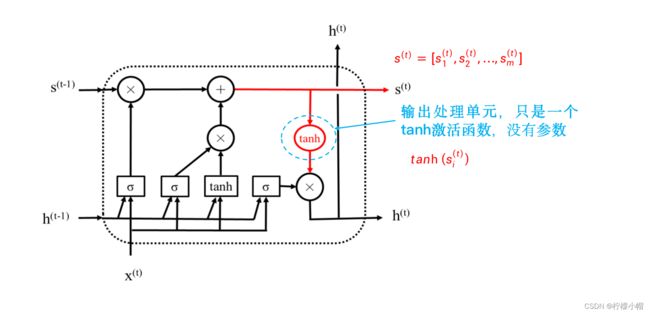
-
输出门和输入门类似,控制模块的输出信息。上图给出了LSTM处理输出信息的示意图。同样,为了表述方便我们称为输出处理单元。但是与输入处理单元不同的是,输出处理单元没有参数,只是简单地用一个tanh激活函数对状态 s ( t ) = [ s 1 ( t ) , s 2 ( t ) , . . . , s m ( t ) ] s^{(t)} = [s_1^{(t)}, s_2^{(t)}, ... , s_m^{(t)}] s(t)=[s1(t),s2(t),...,sm(t)] 进行转换,然后用输出门对其进行选择,得到模块的输出 h ( t ) = [ h 1 ( t ) , h 2 ( t ) , . . . , h m ( t ) ] h^{(t)} = [h_1^{(t)}, h_2^{(t)}, ... , h_m^{(t)}] h(t)=[h1(t),h2(t),...,hm(t)] ,如下图所示。具体计算如下:
h i ( t ) = q i ( t ) t a n h ( s i ( t ) ) h_i^{(t)} = q_i^{(t)}tanh(s_i^{(t)}) hi(t)=qi(t)tanh(si(t))

- 至此介绍完了LSTM,与一般的循环神经网络相比,主要引入了一个状态s,用于传递不同模块之间的信息,通过引入遗忘门、输入门和输出门三个门,对状态、输入和输出进行有针对性的选择。三个门结构上是完全一样的,输入也一样,但是各自有自己的参数,也就是权重,从而实现对不同信息的选择。
- 需要强调的是,LSTM是循环神经网络的一种具体实现,与一般的循环神经网络中子网络是共用的一样,LSTM模块也是共用的,并不是有多个模块横向串联在一起,只是不同的时刻t输入信息不一样,输出也不同。当LSTM处理完一个序列后,最后的输出就是对该序列的一个表达。
- 另外,LSTM还有多个变种,其中最常用的一个简化版是GRU,这里就不一一介绍了,有兴趣的读者请参阅有关资料。
- 但是这样的LSTM应该怎么用呢?
3. 举例:机器翻译
-
与前面介绍过的普通循环神经网络用法一样,事实上,前面说过的所有循环神经网络中的子网络,都可以用LSTM模块代替。模块中的权重等参数也是通过BP算法进行学习的。
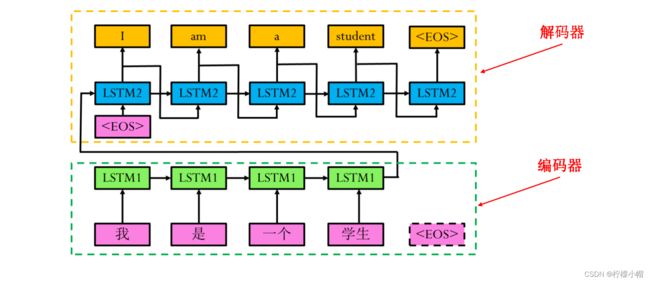
-
上图给出的是一个用LSTM实现的机器翻译示意图,输入是中文“我是一个学生”,输出是英文翻译“I am a student”,其中表示一句话的结束。
-
图中分为编码和解码两部分,绿色虚线框出的是编码部分,输入是一句中文,句中每个词均用词向量表示,经过LSTM处理后,得到这句话的向量表示。黄色虚线框出的是解码部分,将编码后的中文作为输入,经LSTM解码后得到对应的英文。
-
这个就跟序列到序列的循环神经网络是一样的,只是用LSTM模块代替了其中的子网络。
-
LSTM是循环神经网络的一种,前面介绍过的汉语分词、看图说话等中用到的循环神经网络,都可以用LSTM替换。
4. 总结
-
长短期记忆网络LSTM是循环神经网络的一种具体实现,主要是为了解决长序列输入时遇到的梯度消失问题。与一般的循环神经网络相比,LSTM模块引入了一个保持信息传递的状态量s。LSTM模块主要包含了三个处理过程:
-
遗忘过程:通过遗忘门对前一个状态信息进行选择,简单说就是:保留重要的信息,遗忘不重要的信息。
-
记忆阶段:通过输入门对当前的输入信息进行有选择地记忆,也就是说,着重记忆输入信息中有用的信息,减少不重要信息的记忆。选择后的输入信息叠加到状态信息中
-
输出阶段:通过输出门对经过tanh函数处理后的状态信息进行选择,得到模块的输出。
-
-
遗忘门、输入门和输出门三个门的结构是完全一样的,只是分别拥有自己的参数即权重。三个门的输入都是前一个模块的输出和当前输入的拼接,输出是0、1之间的数值,分别构成了不同的选择信号,用于对不同信息的选择。