Codeforces Round #726 (Div. 2)题解A-E1

A. Arithmetic Array

分析：
当sum大于n时，那么添加（sum-n）个0，当sum小于n时，只需要添加一个数即可。

#include 
using namespace std;

int main()
{
    int t; cin >> t;
    while(t--)
    {
        int n; cin >> n;
        int sum = 0;
        for(int i = 0; i < n; i++)
        {
            int tmp; cin >> tmp;
            sum += tmp;
        }
        cout << ((sum>=n)?sum-n:1) << endl;
    }
    // system("pause");
}

B. Bad Boy

分析：
走离起始点较远的两角即可。

#include 
#include 
using namespace std;

int main()
{
    int t; cin >> t;
    while(t--)
    {
        int n, m, x, y; cin >> n >> m >> x >> y;
        if(x > n/2) x = 1; else x = n;
        if(y > m/2) y = 1; else y = m;
        int i, j;
        i = x==1?n:1;
        j = y==1?m:1;
        printf("%d %d %d %d\n",x,y,i,j);
    }
    // system("pause");
}

C. Challenging Cliffs

分析：
排序后，不难发现此时的排列是权重最大的。
但是因为还需要满足约束，开头和末尾的差的绝对值应该最小。
那么我们找到那对数，从中间断开，即可。

#include 
#include 
using namespace std;
int a[300100];
int b[300100];
bool vis[300100];
int abs(int x) { return x<0?-x:x; }
int main()
{
    int t; cin >> t;
    while(t--)
    {
        int n; scanf("%d",&n);
        for(int i = 0; i < n; i++) 
        {
            scanf("%d",&a[i]);
            vis[i] = 0;
        }
        sort(a,a+n);
        int l = 0, r = n-1;
        int x = n-1;
        for( int i = n-1; x>=1&&i>=1; i--)
        {
            if(a[x]-a[x-1] >= a[i]-a[i-1]) x = i;
        }
        swap(a[x],a[x-1]);
        // cout << "x = " << x << endl;
        int cnt = 0;
        for(int i = x; i < n; i++) b[cnt++] = a[i];
        for(int i = 0; i < x; i++) b[cnt++] = a[i];
        for(int i = 0; i < n; i++)
        printf("%d ",b[i]); printf("\n");
    }
}

D. Deleting Divisors

一道博弈论。
分析:
首先考虑1和全体素数是奇异局势, 某一方得到奇异局势时便必败.

然后考虑操作的性质:
不妨设 $x=a\ast b(a,b>1)$
考虑$x-a=a\ast (b-1)$
也就是说一个数x减去自己的约数a, 结果y还是a的倍数; 同时设b为x的约数, 且$b=x/a$, 那么b-1将是结果y的约数.
由此我们可得, 一个奇合数经过一次操作后, 必然会得到一个偶数; 一个(含奇素因子的)偶合数经过一次操作, 可以得到一个奇合数。
这是因为一个偶合数为了操作后得到一个奇数结果, 那么势必把减去所有偶素因子的乘积。 但是因为没有奇素因子所以所有偶素因子的乘积为该数本身，不符合题意约束。

于是我们有了一个初步的模型：

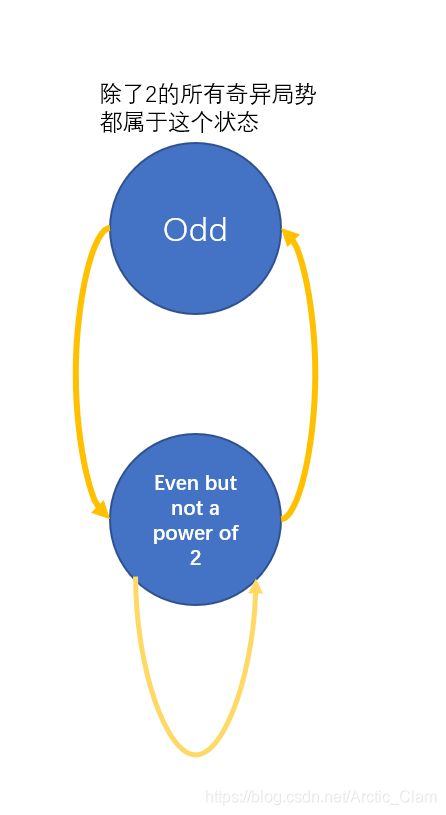
那么再来考虑2的幂次
不妨设$t=2^k(k=1,2,3,...)$

1. 当k=1时:
   先手必败
2. 当k=2时:
   先手必胜
3. 当k>2时,有两种操作:
   1). $t=t-2^i(i=1,2,...,k-2)$. 此时t为变为一个不是2的幂次的偶数, 因此这种操作对方必胜.
   2). $t=t-2^{k-1}$. 此时t变为2的幂, 且幂次-1.

不难看出当k为奇数的时候, 先手必败, k为偶数的时候后手必败.
于是给出修正后的模型

代码:

#include 
using namespace std;

int main()
{
    int t; scanf("%d",&t);
    while(t--)
    {
        int n; scanf("%d",&n);
        int cnt = 0;
        while(n%2==0) { n/=2; cnt++; }
        if(cnt == 0) printf("Bob\n"); //odd
        else if(cnt == 1 && n == 1) printf("Bob\n"); //exactly be 2
        else if(n > 1) printf("Alice\n"); //even but not a pow of 2
        else if((cnt & 1) == 0) printf("Alice\n"); 
        else printf("Bob\n");
    }
}

E1. Erase and Extend (Easy Version)

分析:
暴力枚举所有前缀形成的串, 取字典序最小的即可.
时间复杂度$O(n^2)$

#include 
#include 
#include 
using namespace std;
char s[100001], t[100001], ans[100001];
int n, k; 
bool cmp()
{
    for(int i = 0; i < k; i++)
    {
        if(ans[i] > t[i]) return 1;
        else if(ans[i] == t[i]) continue;
        else return 0;
    }
    return 0;
}
int main()
{
    cin >> n >> k;
    scanf("%s",s);
    for(int i = 1; i <= n; i++)
    {
        int cnt = k/i + (k%i!=0);
        for(int j = 0; j < cnt; j++)
        {
            for(int l = 0; l < i; l++)
                t[i*j+l] = s[l];
        }
        t[k] = '\0';
        if(i>1) 
        {
            if(cmp()) strcpy(ans, t);
        }
        else strcpy(ans, t);
        // printf("this t is %s\n",t);
    }
    printf("%s\n",ans);
    // system("pause");
}