Codeforces Round #818 (Div. 2) A - D题解

Codeforces Round #818 (Div. 2) A - D题解

A

题意

找出共有多少对数(a, b), 满足 $\frac{lcm(a,b)}{gcd(a,b)}\le 3$ ,其中$1\le a,b\le 3$

思路

显然 lcm(a, b) = x * gcd(a, b) <= 3 * gcd(a, b)，显然假如a >= b，当a为b的1、2、3倍时满足条件

代码

void solve()
{
    int n;
    cin >> n;
    cout << n + n / 2 * 2 + n / 3 * 2 << '\n';
}

B

题意

在nn的方格中要求任意1k或k*1的格子中存在至少一个’X’，和给出的第r行c列必须为’X’，题目保证给出的n是k的倍数。

思路

对于每行来说保证两个’X’之间最多间隔k - 1个格子，由于n是k的倍数，可以发现当‘X’上下交错安放时满足条件

代码

const int N = 505;
char a[N][N];
int n, k, r, c;
 
void solve()
{
    memset(a, '.', sizeof(a));
    cin >> n >> k >> r >> c;
    int d = n / k;
    --r, --c;
 
    for (int i = 0, p = r; i < n; ++i, c = (c + 1) % n, p = (p + 1) % n)
    {
        for (int j = 0, q = c; j < d; ++j, q = (q + k) % n)
            a[p][q] = 'X';        
    }
 
 
    for (int i = 0; i < n; ++i) a[i][n] = 0;
    for (int i = 0; i < n; ++i) cout << a[i]<< '\n';
}

C

题意

给出数组a和b，在一个操作中如果 $a_i\le a_{(i+1)\%n}$，则$a_i=a_i+1$判断是否能进行操作使得数组a等于b。

思路

首先a不能减小，因此需满足 $a_i\le b_i$，其次当 $a_i!=b_i$时需要$b_i\le b_{(i+1)\%n}+1$才能构造。接下来证明只需要满足这些条件即可构造出来：
在进行操作时假如说$a_i>a_{i+1}$我们可以想象出一条边从 $a_{i+1}$指向$a_i$，显然图中没有环，就可以按照拓扑序列进行相加，使得序列满足要求。

代码

const int N = 2e5 + 10;
int a[N], b[N], n;
 
void solve()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0; i < n; i++) cin >> b[i];
    for (int i = 0; i < n; i++) 
    {
        int j = (i + 1) % n;
        if (a[i] > b[i] || (a[i] != b[i] && b[i] > b[j] + 1)) return cout << "NO\n", void(0); 
    }
    cout << "YES\n";
}

D

题意

共有$2^n$个人进行比赛，按顺序两两pk胜者进入下一轮。Madoka可以任意安排开始时人员顺序，以及每轮中时是左边获胜还是右边获胜，而最终获胜的人序号越靠前，他赢得越多。而比赛方可以选择交换最多k对人，使得Madoka赢得少一些，问Madoka能保证自己安排到的最小编号是几。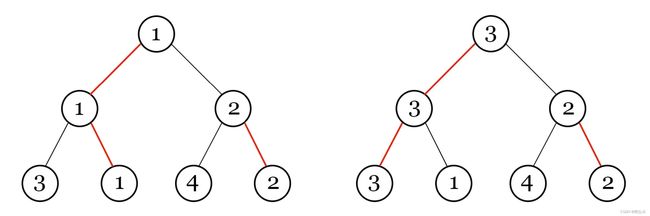

思路

因为一个点的左右子树交换不影响结果，为了方便观察，将所有选择转到左子树，从根结点沿着选择的边所到达的叶子结点即为获胜者，每次选择则是将路径转向右子树，因此在k次选择中${\sum }_{i=0}^k{\text{C}}_n^i$即为能选择到的点，因此Madoka将这些点的值设为较小值，即为答案

代码

const ll mod = 1e9 + 7;
const int N = 1e5 + 10;
ll ji[N];
 
ll C(const int& a, const int& b)
{
    return ji[a] * inv(ji[b], mod) % mod * inv(ji[a - b], mod) % mod;
}
 
void init()
{
    ji[0] = 1;
    for (ll i = 1; i < N; ++i) ji[i] = ji[i - 1] * i % mod;
}