排序算法之时间复杂度nlogn

上一篇博客讲解了时间复杂度为$O(n^2)$的三种算法。但是真正封装起来的排序算法是优化之后的快排等时间复杂度$O(nlo{g}_2^n)$。动画算法APP链接点解上一篇博客

快速排序

快速排序的基本思想是基于分治策略的，基本思想如下：

• 分解：先从序列中取出一个元素作为基准，以基准元素为标准将序列分解为两个子序列。其中小于或等于基准的子序列在左侧，大于基准的子序列在右侧。
• 治理：对拆分之后的子序列进行快速排序
• 合并：将排序好的子序列合并在一起，从而得到整个序列的排序。
  这像是我们常说的“大事化小，小事化了”，大的困难分解成一个个小的问题，逐个击破。
  分治法后面也会讲解
  常见的基准元素选取方式有：选择第一个元素，最后一个元素，中位数等等。

源代码

#include

using namespace std;
//获取基准元素所在的位置 
int GetMid(int arr[], int low, int high)
{
	int i = low, j = high, pivot = arr[low];
	while (i < j)//交换后继续扫描 
	{
		while (i<j&&arr[j]>pivot) j--;//右侧开始查找比基准元素更小的值 
		while (i < j&&arr[i] <= pivot) i++;//左侧查找比基准元素大于等于的值 
		if (i < j)
		{
			swap(arr[i++], arr[j--]);//先交换后赋值 
		}
	}
	if (arr[i] > pivot)
	{
		swap(arr[i - 1], arr[low]);//在代码中提供的示例中，在遇到第一次扫描时交换i和j都指向37。如果不加最后的判断会出现错误。 
		return i - 1;
	}
	swap(arr[i], arr[low]);
	return i;
}
//快速排序函数
void QuickSort(int arr[], int low, int high)
{
	int mid;
	if (low < high)
	{
		//递归快排
		mid = GetMid(arr, low, high);
		QuickSort(arr, mid + 1, high);//右区间快排
		QuickSort(arr, low, mid - 1);//左区间快排
	}
}

int main()
{
	int N = 9;
	int arr[9] = { 30,24,5,58,37,36,12,42,39 };
	for (int i = 0; i < N; i++)
	{
		cout << arr[i] << ",";
	}
	cout<<endl; 
	QuickSort(arr, 0, N-1);
	for (int i = 0; i < N; i++)
	{
		cout << arr[i] << ",";
	}
	cout << endl;
}

合并排序

合并排序采用的就是分治策略，讲一个大的问题分成很多的小问题。先解决小问题，然后通过小问题解决大问题。

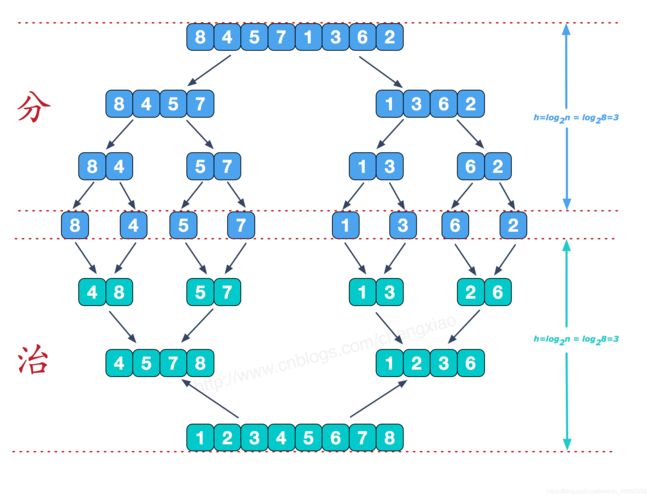
通过将每一个分解的子序列排序，然后不断的递归子序列合并。达到总序列的有序排列。合久必分，分久必合就是合并排序的策略。

源代码

#include

using namespace std;


//最小单元序列的合并
void Merge(int arr[],int low,int mid, int high)
{
	//1.申请与arr等长的数组B
	int *B = new int[high - low + 1];
	int i = low, j = mid + 1, k = 0;
	//2.将arr数组一分为二，按照升序的规则将元素依次放到B数组中
	while (i<=mid&&j<=high)
	{
		if (arr[i] <= arr[j])
		{
			B[k++] = arr[i++];
		}
		else
		{
			B[k++] = arr[j++];
		}
	}
	//3.将arr数组的升序未排序的部分复制到B，左侧和右侧
	while (i <= mid){ B[k++] = arr[i++]; }
	while (j <= high){ B[k++] = arr[j++]; }
	//4.将B数组复制到arr数组，释放B
	for (i = low, k = 0; i <= high; i++)
	{
		arr[i] = B[k++];
	}
	delete []B;
}

//合并排序
void MergeSort(int arr[],int low,int high)
{
	//递归合并排序
	if (low < high)
	{
		int mid = (low + high) / 2;
		MergeSort(arr, low, mid);
		MergeSort(arr, mid + 1, high);
		Merge(arr, low, mid, high);
	}
}


int main()
{
	int N = 8;
	int a[8] = { 42,15,20,6,8,38,50,12 };
	MergeSort(a, 0, N-1);
	for (size_t i = 0; i < N; i++)
	{
		cout << a[i] << ",";
	}
}

时间复杂度

其中快速排序的平均时间复杂度为$O(nlo{g}^n)$。合并排序的二叉树高度为$lo{g}_2^n$，每一层都是n个元素进行比较，所以总的时间复杂度为$O(nlo{g}^n)$