递推、迭代、递归入门
递推、迭代、递归入门
递推和递归是用计算机解决问题的两种基本方法,最能体现计算机程序解决问题的特点。两种方法并无本质区别,只不过思考问题的方向不同。递推是从小到大,递归是从大到小。打个比方:如果要建造一个10层的楼房,递推是先建好第1层,再建第2层,再建第三层,直到第10层为止。递归是这样思考的:我要建第10层,你给我一个9层的楼房,我在上面加一层就是10层了,如不没有9层的楼房,给我一个8层的,我先加一层就是9层了…,如此还是要建第一层。
递推符合人的思考习惯,一般效率较高。递归的效率一般不如递归,但递归是计算机编程的重要思想,我们解决问题不妨从递推和递归两方面都考虑。
递推使用循环,递归使用栈(隐含的循环)
迭代不断使用变量的旧值推导出新值的过程,这一点与递推是一样的,递推一般要用到数组,会占用一定的空间,但更直观;迭代反复使用变量,占用空间较少。
理解了递推和递归,编程可算是入门了。
下文从最简单问题开始,逐步过渡到较难的问题。
1、等差数列的递推和递归:输出等差数列1 3 5 7 9 的第n项。
递推:第一项是1,后一项是前一项加2,递推关系是:a[n]=a[n-1]+2
#include
using namespace std;
int a[100];
int main(){
int n;
cin>>n;
a[1]=1;
for(int i=2;i<=n;i++) {
a[i]=a[i-1]+2;
}
cout< 迭代
#include
using namespace std;
int main(){
int n;
cin>>n;
int a=1;
for(int i=2;i<=n;i++){
a=a+2;
}
cout< 递归:1.f(n)表示数列的第n项 2、后一项是前一项加2,递归关系是:f(n)=f(n-1)+2 3、边界条件,当n==1时,值是1。
#include
using namespace std;
int f(int n){
if (n==1) return 1;
return f(n-1)+2;
}
int main(){
cout< 2、等比数列的递推和递归:输出等比数列1 2 4 8…的第n项
递推:第一项是1,后一项是前一项乘2,递推关系是:a[n]=a[n-1]*2
#include
using namespace std;
int a[100];
int main(){
int n;
cin>>n;
a[1]=1;
for(int i=2;i<=n;i++) {
a[i]=a[i-1]*2;
}
cout< 迭代
#include
using namespace std;
int main(){
int n;
cin>>n;
int a=1;
for(int i=2;i<=n;i++){
a=a*2;
}
cout< 递归:1.f(n)表示数列的第n项
2、后一项是前一项乘2,递归关系是:f(n)=f(n-1)*2
3、边界条件,当n==1时,值是1。
#include
using namespace std;
int f(int n){
if (n==1) return 1;
return f(n-1)*2;
}
int main(){
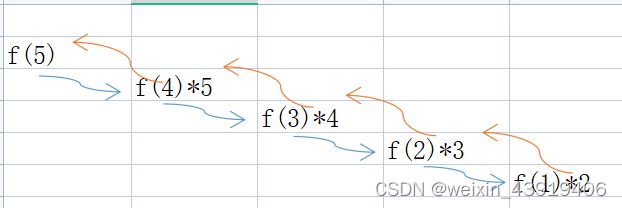
cout< 3、n的阶乘$n!=1 * 2 * 3…
递推:第一项是1,后一项是前一项乘n,递推关系是:a[n]=a[n-1]*n
#include
using namespace std;
int a[100];
int main(){
int n;
cin>>n;
a[1]=1;
for(int i=2;i<=n;i++) {
a[i]=a[i-1]*i;
}
cout< 迭代
#include
using namespace std;
int main(){
int n;
cin>>n;
int a=1;
for(int i=2;i<=n;i++){
a=a*i;
}
cout< 递归:1.f(n)表示1到n项的乘积
2、后一项是前一项乘n,递归关系是:f(n)=f(n-1)*n
3、边界条件,当n==1时,值是1。
#include
using namespace std;
int f(int n){
if (n==1) return 1;
return f(n-1)*n;
}
int main(){
cout< 4、辗转相除法求两数的最大公约数
递推:
#include
using namespace std;
int a[100];
int main(){
int m,n;
cin>>m,n;
a[1]=m;
a[2]=n;
int t=1;
while(a[t]%a[t+1]){
a[t+2]=a[t]%a[t+1];
t++;
}
cout< 迭代:t=a%b,b的值给a,t的值给b,再进行下一次迭代
#include
using namespace std;
int main(){
int a,b,t;
cin>>a>>b;
while (a%b!=0){
t=a%b;
a=b;
b=t;
}
cout< 递归:1、定义f(a,b)为a和b两数的最大公约数
2、边界 如果a%b==0 得到最大公约数b
3、如果a%b不等于0,求b和a%b的最大公约数
#include
using namespace std;
int f(int a,int b){
if (a%b==0) return b;
return f(b,a%b);
}
int main(){
int a,b;
cin>>a>>b;
cout< 5、上台阶1:楼梯有n(71>n>0)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,编程计算共有多少种不同的走法。
迭代:第1级楼梯有1中走法;第2级楼梯有2中走法,可以1步1步上去,也可以一下跨两步;第3级楼梯由第1级楼梯跨2步上来或第2级台阶跨1步上来,有1+2,3中走法,有人可能会问,第3级不可以由第1级一步一步上来吗?是的可以,1级楼梯上来1步,就到了第2级台阶,这种走法已经包含在第2级台阶的走法中了;n级台阶可以由n-1级跨2步上来或由n-2级跨一步上来,a[n]=a[n-1]+a[n-2]
递推
#include
using namespace std;
int a[100];
int main(){
int n;
cin>>n;
a[1]=1;
a[2]=2;
for(int i=3;i<=n;i++){
a[i]=a[i-1]+a[i-2];
}
cout< 迭代
#include
using namespace std;
int main(){
int n,a,b,t;
a=1;
b=2;
cin>>n;
if(n<3) {
cout< 递归:1、定义f(n)表示到n级台阶的走法
2、n级台阶可以由n-1级跨2步上来或由n-2级跨一步上来,f(n)=f(n-1)+f(n-2)
3、边界:n=1 有一种方法,n=2有2种方法
#include
using namespace std;
int f(int n){
if (n==1) return 1;
if (n==2) return 2;
return f(n-1)+f(n-2);
}
int main(){
int n;
cin>>n;
cout< 6、上台阶2:楼梯有n(71>n>0)阶台阶,上楼时可以一步上1阶,也可以一步上2阶,也可以一步上3阶,编程计算共有多少种不同的走法。
递推,就是前一题的扩展。分析方法类似。
#include
using namespace std;
int a[100];
int main(){
a[1]=1;
a[2]=2;
a[3]=4;
int n;
cin>>n;
for(int i=4;i<=n;i++){
a[i]=a[i-1]+a[i-2]+a[i-3];
}
cout< 迭代
#include
using namespace std;
long long tj(int n)
{
if (n<=2) return n;
if (n==3) return 4;
long long a=1,b=2,c=4;
long t;
for(int i=4;i<=n;i++)
{
t=a+b+c;//
a=b;//b的值给a
b=c;//c的值给b
c=t;//t的值给c
}
return c;
}
int main()
{
int x;
while(cin>>x && x)
{
cout< 递归
#include
using namespace std;
int f(int n){
if (n==1) return 1;
if (n==2) return 2;
if (n==3) return 4;
return f(n-1)+f(n-2)+f(n-3);
}
int main(){
int n;
cin>>n;
cout< 7、信息学奥赛一本通 1312:昆虫繁殖:科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过x个月产卵),问过z个月以后,共有成虫多少对?0≤x≤20,1≤y≤20,X≤z≤500。
递推:第1个月有一对成虫,过x月后产卵,卵要两个月长成成虫,则在x+2月内只有一对成虫。以后每月的成虫数包括两不分,一部分是一起不死的成虫,另一部分是x+2月前的卵长成的成虫。递推公式是:a[n]=a[n-1]+a[n-(x-2)]
复制代码到粘帖板
#include
using namespace std;
long c[100];
int main(){
long long x,y,z;
cin>>x>>y>>z;
for(int i=1;i<=x+2;i++){
c[i]=1;
}
for(int i=x+3;i<=z+1;i++){
c[i]=c[i-1]+c[i-(x+2)]*y;
}
cout< 递归:1、f(n,x,y) 表示n个月后有多少对成虫,x表示成熟后x月开始产卵,y表示每次产多少对卵
2、递推关系:f(n-1,x,y)+f(n-(x+2),x,y)*y
3、边界条件:x+2月前只有一对成虫
#include
using namespace std;
long long f(int n,int x,int y){
if (n<=x+2) return 1;
return f(n-1,x,y)+f(n-(x+2),x,y)*y;
}
int main(){
int n,x,y;
cin>>x>>y>>n;
cout< 8、信息学奥赛一本通:1196踩方格:
【题目描述】
有一个方格矩阵,矩阵边界在无穷远处。我们做如下假设:
a、每走一步时,只能从当前方格移动一格,走到某个相邻的方格上;
b、走过的格子立即塌陷无法再走第二次;
c、只能向北、东、西三个方向走;
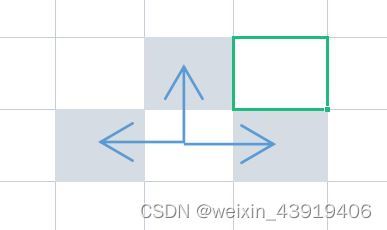
请问:如果允许在方格矩阵上走n步,共有多少种不同的方案。2种走法只要有一步不一样,即被认为是不同的方案。
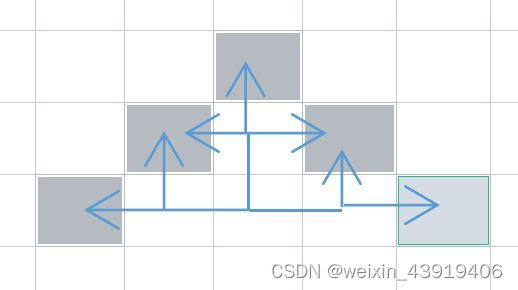

【方法1】递推:
如果走一步,有3种;如果走2步,有7种走法;如果走三步有17种。如果上一步是向上的,可以左右上;上一步是向左的,只能上左;上一步是向右的,只能上右。设up[i]表示向上,left[i]表示向左,right[i]表示向右,则up[i]=up[i-1]+left[i-1]+right[i-1],left[i]=left[i-1]+up[i-1],right[i]=right[i-1]+up[i-1]。
#include 方法2:递推
设a[i]为第走i步有几种走法,a[i]=left[i]+right[i]+up[i]=left[i-1]+up[i-1]+right[i-1]+up[i-1]+left[i-1]+up[i-1]+right[i-1]=2*(left[i-1]+up[i-1]+right[i-1)+up[i-1]=2a[i-1]+up[i-1]=2a[i-1]+(left[i-2]+right[i-2]+up[i-2])=2*a[i-1]+a[i-2]
#include 方法3:递归
#include