跟着Nature Medicine学作图--箱线图+散点图
从这个系列开始,师兄就带着大家从各大顶级期刊中的Figuer入手,从仿照别人的作图风格到最后实现自己游刃有余的套用在自己的分析数据上!这一系列绝对是高质量!还不赶紧点赞+在看,学起来!
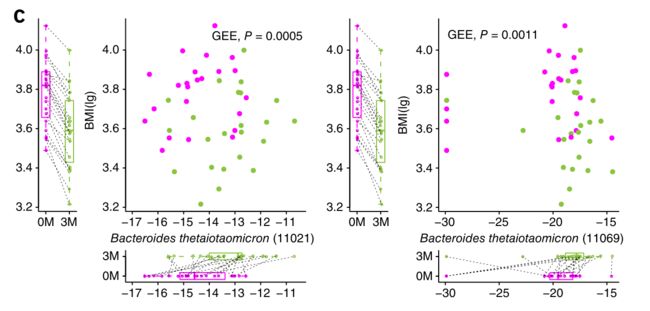
本期分享的是昨天更新的Nature Medicine上面那篇文章中的一个箱线图和散点图。
之所以讲这张图是因为这张图既通过散点图描绘了两组样本点的分布差异,同时在X和Y两个尺度上分别绘制箱线图,既反映了两组在X和Y两个尺度上的显著差异,也更好的阐述了X和Y的相关关系。此外箱线图还加上了连线,显示出了从术后1天,到术后3个月的变化趋势,非常好的呈现方式,值得大家学习!
话不多说,直接上图!
示例数据和代码获取
读图
这张图通过广义估计方程(GEE)分析,发现在袖状胃切除(SG)治疗后B. thetaiotaommicron丰度的增加与BMI的下降相关。
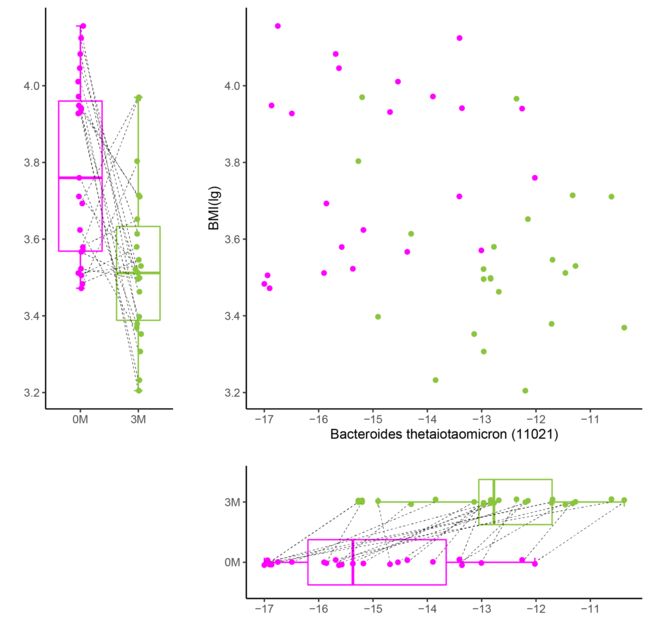
效果预览
示例数据和R包载入
# 加载包:
library(ggplot2)
# 读取数据:
new_data <- read.csv("data01.csv")
> new_data
Bacteroides_thetaiotaomicron BMI group group2
1 -13.36254 3.941414 group_0M sample1
2 -16.49327 3.927730 group_0M sample2
3 -15.85773 3.692952 group_0M sample3
4 -16.86678 3.948474 group_0M sample4
5 -15.57506 3.579352 group_0M sample5
6 -12.02062 3.759882 group_0M sample6
7 -16.75177 4.155833 group_0M sample7
8 -15.62603 4.045753 group_0M sample8
9 -13.00599 3.570529 group_0M sample9
10 -15.37026 3.522664 group_0M sample10
11 -14.68648 3.931393 group_0M sample11
12 -13.89668 3.971936 group_0M sample12
13 -16.94041 3.505565 group_0M sample13
14 -15.68604 4.082791 group_0M sample14
15 -13.40720 4.124388 group_0M sample15
绘制
- 首先绘制最中间的散点图:
# 绘制散点图:
ggplot(new_data)+
# 绘制基本散点图
geom_point(aes(Bacteroides_thetaiotaomicron, BMI,color=group))+
# 设置颜色
scale_color_manual(values = c(group_0M="#ff00ff", group_3M="#8ac53e"))+
# 设置主题
theme_classic()+
# 设置坐标轴范围
scale_x_continuous(breaks = c(-17:11))+
scale_y_continuous(breaks = seq(3.2,4.0,0.2))+
# 设置x轴和y轴标签
xlab("Bacteroides thetaiotaomicron (11021)")+
ylab("BMI(lg)")+
# 去掉图例:
theme(legend.position = 'none')
ggsave(filename = "scatter_plot.pdf",height=5,width = 5)
- 再绘制左边的箱线图
# 绘制左边的箱线图:
ggplot(new_data,aes(group, BMI))+
# 加上误差棒;由于自带的箱形图没有胡须末端没有短横线,使用误差条的方式补上
stat_boxplot(geom = "errorbar",width=0.15,aes(color=group))+
# 绘制基本箱线图
geom_boxplot(aes(color=group),fill="white")+
# 加上散点之间的连线
geom_line(aes(group=group2), color="black",linetype="dashed",size=0.2, alpha=0.8)+
# 箱线图加散点
geom_jitter(aes(color=group,fill=group),width =0.05,shape = 21)+ #设置为向水平方向抖动的散点图,width指定了向水平方向抖动,不改变纵轴的值
# 设置颜色
scale_color_manual(values = c(group_0M="#ff00ff", group_3M="#8ac53e"))+
scale_fill_manual(values = c(group_0M="#ff00ff", group_3M="#8ac53e"))+
# 设置主题
theme_classic()+
# 设置坐标轴范围
scale_x_discrete(labels=c("0M","3M"))+
scale_y_continuous(breaks = seq(3.2,4.0,0.2))+
# 设置x轴和y轴标签
xlab("")+
ylab("")+
# 去掉图例:
theme(legend.position = 'none')
ggsave(filename = "left_boxplot.pdf",height=5,width = 2)
- 最后绘制下方的箱线图
# 绘制下面的箱线图:
ggplot(new_data,aes(group, Bacteroides_thetaiotaomicron))+
# 加上误差棒;由于自带的箱形图没有胡须末端没有短横线,使用误差条的方式补上
stat_boxplot(geom = "errorbar",width=0.15,aes(color=group))+
# 绘制基本箱线图
geom_boxplot(aes(color=group),fill="white")+
# 加上散点之间的连线
geom_line(aes(group=group2), color="black", linetype="dashed", size=0.2, alpha=0.8)+
# 箱线图加散点
geom_jitter(aes(color=group,fill=group),width =0.05,shape = 21)+ #设置为向水平方向抖动的散点图,width指定了向水平方向抖动,不改变纵轴的值
# 设置颜色
scale_color_manual(values = c(group_0M="#ff00ff", group_3M="#8ac53e"))+
scale_fill_manual(values = c(group_0M="#ff00ff", group_3M="#8ac53e"))+
# 设置主题
theme_classic()+
# 设置坐标轴范围
scale_x_discrete(labels=c("0M","3M"))+
scale_y_continuous(breaks = c((-17):(-11)))+
# 设置x轴和y轴标签
xlab("")+
ylab("")+
# 去掉图例
theme(legend.position = 'none')+
# 旋转坐标轴
coord_flip()
ggsave(filename = "down_boxplot.pdf",height=2,width = 5)
- 最后,用AI将三个图拼接在一起就完事啦!
结果展示
示例数据和代码获取