【笔记3-6】CS224N课程笔记 - RNN和语言模型

【笔记3-1】CS224N课程笔记 - 深度自然语言处理
【笔记3-2】CS224N课程笔记 - 词向量表示 word2vec
【笔记3-3】CS224N课程笔记 - 高级词向量表示
【笔记3-4】CS224N课程笔记 - 分类与神经网络
【笔记3-5】CS224N课程笔记 - 依存分析
【笔记3-7】CS224N课程笔记 - 神经机器翻译seq2seq注意力机制
【笔记3-8】CS224N课程笔记 - 卷积神经网络

CS224n：深度学习的自然语言处理（2017年冬季）1080p https://www.bilibili.com/video/av28030942/

关键词：语言模型，RNN，双向RNN，deep RNN，GRU，LSTM

语言模型

语言模型介绍

语言模型用于计算序列当中一系列单词出现的概率。单词产生的概率与之前生成过的单词有关，并且是在一定窗口范围内有关，而不是与所有产生过的词语相关。因此序列生成概率可以表示为：$$P(w_1,...,w_m)=\prod _{i=1}^{m}P(w_i|w_1,...,w_{i-1})\approx \prod _{i=1}^{m}P(w_i|w_{i-n},...,w_{i-1})$$这一概率计算方法对于语音和翻译系统在确定单词序列是否为输入句子的准确翻译时特别有用。在现有翻译系统中，对于每个短语/句子，软件都会生成一系列可选的单词序列并对它们进行评分，以确定最可能的翻译序列。

在机器翻译中，模型为每个备选的输出词序列分配一个优等性评分来为输入短语选择最佳词序。它通过一个概率函数为每个候选项分配一个分数，得分最高的序列是翻译的输出。如，与“small the is cat”相比，“the cat is small”得分更高;与“walking house after school”相比，“walking home after school”得分更高。

n-gram

为了计算上述概率，可以将每个n-gram的计数与每个单词的频率进行比较，称为n-gram语言模型。例如，如果模型采用bi-gram，则通过将一个单词与其前一个单词结合计算得到的每个bi-gram的频率将除以相应的uni-gram的频率，用这种思路可以得到bigram和trigram计算方法：$$\begin{gathered} P(w_2|w_1)=\frac{count(w_1,w_2)}{count(w_1)} \\ P(w_3|w_1,w_2)=\frac{count(w_1,w_2,w_3)}{count(w_1,w_2)} \end{gathered}$$上述方程的计算思路是：基于一个固定的上下文窗口(前n个单词)预测下一个单词。但是某些情况下，n个单词的窗口可能不足以捕获上下文。例如“As the proctor started the clock, the students opened their…”。如果窗口为3，“students opened their”，那么基于语料库计算的概率可能提示下一个单词是“books”，然而如果n足够大，使得上下文包含“proctor”，则可能会选择“exam”。

这就引出了n-gram的两个问题：稀疏性和存储问题。

• 稀疏性问题
  模型的稀疏性问题源于两个方面。
  首先，如果$w_1,w_2,w_3$从未同时出现在语料库中，则$w_3$出现的概率为0。解决这个问题可以在词汇表中每个单词的计数中添加一个较小的$\sigma$，称为平滑。其次，如果$w_1,w_2$在语料库中没有一起出现过，就无法计算$w_3$的概率。解决这个问题可以只对$w_2$设定条件，称为后退。n的增加使稀疏性问题变得更糟。通常n = 5。
• 存储问题
  需要存储在语料库中看到的所有n-gram的计数。随着n的增加(或者语料库大小的增加)，模型的大小也随之增加。

基于窗口的神经语言模型

Bengio等人在神经概率语言模型中首次解决了上述问题，提出了大规模的自然语言处理深度学习模型。该模型学习单词的分布式表示，以及用这些表示来表示的单词序列的概率函数。下图显示了相应的神经网络架构。输入的词向量同时供隐藏层和输出层使用。

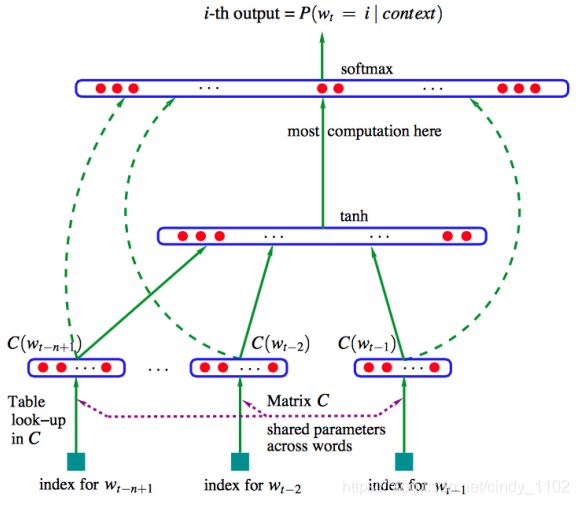
图中的softmax函数可以写成：（注意式子中各个权重矩阵的训练对象）$$\hat{y}=softmax(W^{(2)}tanh(W^{(1)}x+b^{(1)})+W^{(3)}x+b^{(3)})$$上述模型可以用下述模型图简要表示：

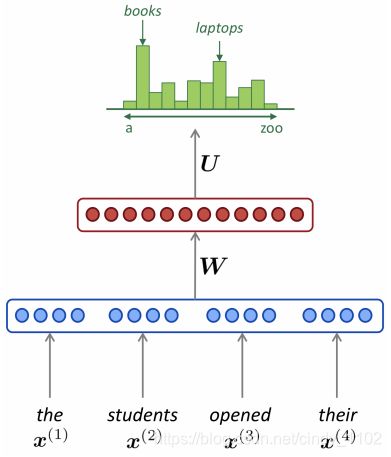
RNN

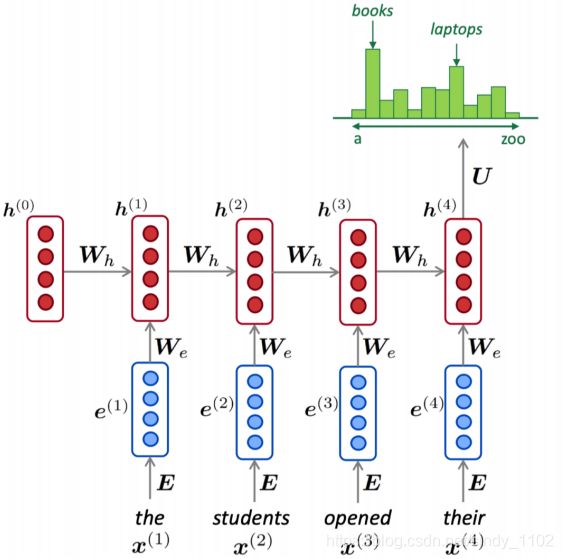
传统的翻译模型只考虑一定窗口内的先前词汇，而RNN能对语料库中所有的先前词汇进行处理。

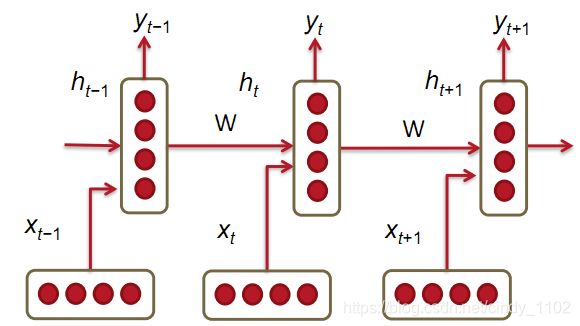
上图为RNN的结构，其中垂直矩形框是时间步长t处的隐藏层，每个隐藏层包含多个神经元，每个神经元对其输入进行线性矩阵运算，然后进行非线性运算(如tanh())。在每个时间步长中，隐藏层有两个输入：前一层的输出$h_{t-1}$和该时刻的输入$x_t$。通过softmax获得预测输出下一个单词：$$\begin{gathered} h_t=\sigma (W^{(hh)}{h}_{t-1}+W^{(hx)}{x}_{[t]}) \\ \hat{y}=softmax(W^{(S)}{h}_t) \end{gathered}$$计算过程用图形表示如下：

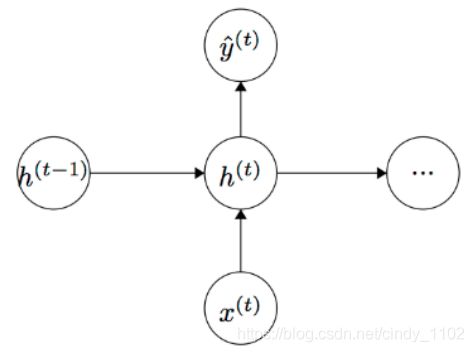
这里需要注意的是，在整个过程中学习的权重$W^{(hh)},W^{(hx)}$是一样的，因此减少了需要学习的参数数量，并且参数的数量与输入序列的长度无关，因此不会出现n-gram存在的问题。

前面描述过的例子用RNN 模型来处理，如下图所示：

RNN Loss and Perplexity

RNN一般采用交叉熵作为损失计算方式$$\begin{gathered} J^{(t)}(\theta )=-\sum _{j=1}^{|V|}{y}_{t,j}log({\hat{y}}_{t,j}) \\ J=\frac{1}{T}\sum _{t=1}^T{J}^{(t)}(\theta )=-\frac{1}{T}\sum _{t=1}^T\sum _{j=1}^{|V|}{y}_{t,j}log({\hat{y}}_{t,j}) \end{gathered}$$Perplexity是一种测量混淆程度的方法，较低的值意味着对预测序列中的下一个单词更有信心(与ground truth结果相比)，RNN对应的perplexity为$$perplexity=2^J$$也就是说损失函数值越小，perplexity的值越小，相应的结果的不确定性越低。

RNN的优缺点及应用

优点：

1. 可以处理任意长度的输入序列
2. 对于较长的输入序列长度，模型大小不会增加
3. 步骤t的计算(理论上)可以使用来自多个步骤的信息。
4. 对输入的每个时间步都应用相同的权重，因此在处理输入时具有对称性

缺点：

1. 计算很慢——因为它是顺序的，所以不能并行化
2. 在实践中，由于渐变消失和爆炸等问题，很难从许多步骤返回信息

运行一层RNN所需的内存与语料库中的单词数量成正比。把一个句子看成一个小批量，一个有k个单词的句子就有k个要存储在内存中的单词向量。同样，RNN必须保持两对W, b矩阵。如前所述，虽然W可能非常大，但它不随语料库的大小而伸缩(与传统的语言模型不同)。对于一个有1000个递归的RNN层，无论语料库大小，矩阵都是1000*1000。

RNN可用于许多任务，如标记(如词性标注、命名实体识别)、句子分类(如情绪分类)和编码模块(如问答、机器翻译)。

梯度消失和梯度爆炸问题

RNN将权重矩阵从一个时间步长传播到下一个时间步长。实现的目标是通过遥远的时间步长来传播上下文信息。例如，考虑以下两句话：
(1) “Jane walked into the room. John walked in too. Jane said hi to ___”

(2) “Jane walked into the room. John walked in too. It was late in the day, and everyone was walking home after a long day at work. Jane said hi to ___”

根据上下文，可以看出两个空白点的答案很可能是“John”。在实践中，RNN更有可能正确预测句子1中的空白点。这是因为在反向传播阶段，梯度值的贡献随着传播到更早的时间步长而逐渐消失。因此，对于长句，“John”被识别为下一个单词的可能性随上下文的增长而降低。下面讨论消失梯度问题背后的数学推导。

梯度消失/爆炸问题的解决方法

既然我们已经对消失梯度问题的本质和它在深度神经网络中的表现有了直观的认识，那么让我们关注一个简单而实用的启发式方法来解决这些问题。
为了解决梯度爆炸的问题，Thomas Mikolov首先引入了一个简单的启发式解决方案，当梯度爆炸时，将梯度裁剪为一个小数值。也就是说，当它们达到某个阈值时，就会被重新设置为一个小数值，如下述算法所示。

下图展示了这一算法的效果。图中给出了一个小型RNN的W矩阵决策面及其偏置项b。该模型由一个RNN单元通过少量的时间步长构成；实心箭头显示了每个梯度下降步骤的训练进度。当梯度下降模型遇到目标函数中的高误差壁时，梯度被推到决策面较远的位置。而裁剪模型生成虚线，在虚线中，它将错误梯度拉回到接近原始梯度的位置。

为了解决梯度消失问题，引入两种技术。
第一种技术从一个单位矩阵初始化W(hh)，而不是随机初始化W(hh)。
第二种方法是使用校正线性单元(ReLU)代替sigmoid函数。ReLU的导数不是0就是1。通过这种方式，梯度将流经导数为1的神经元，而不会在向后传播时衰减时间步长。

Deep Bidirectional RNN

前面关注的是基于过去单词来预测下一个单词的RNN。通过将RNN模型倒读语料库，可以根据将来的单词做出预测。双向深度神经网络在每个时间步t，有两个隐藏层，一个用于从左到右传播，另一个用于从右到左传播。为了保留两个隐藏层，网络的权值和偏置参数消耗的内存空间是原来的两倍。最终结合两个方向RNN隐藏层的结果生成最终的分类结果。下图为双向RNN网络结构：
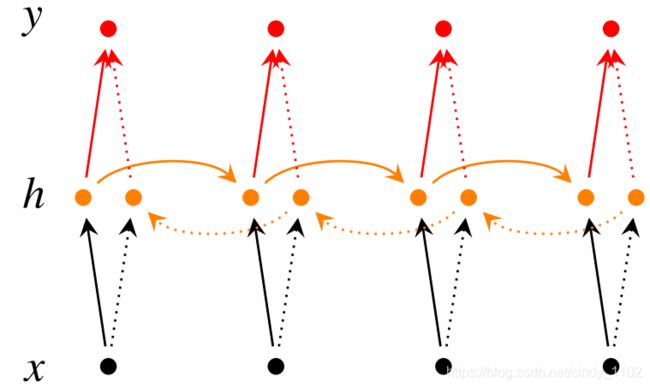建立双向RNN隐层及预测的数学公式如下：
$$\begin{gathered} {\underset{h}{\to }}_t=f(\underset{W}{\to }{x}_t+\underset{V}{\to }{\underset{h}{\to }}_{t-1}+\underset{b}{\to }) \\ {\underset{h}{\leftarrow }}_t=f(\underset{W}{\leftarrow }{x}_t+\underset{V}{\leftarrow }{\underset{h}{\leftarrow }}_{t+1}+\underset{b}{\leftarrow }) \\ \hat{y}=g(U{h}_t+c)=g(U[{\underset{h}{\to }}_t;{\underset{h}{\leftarrow }}_t]+c) \end{gathered}$$RNN也可以是多层的。如下图展示的多层双向RNN，其中每个较低的层向下一层提供信息。如图所示，在这个网络结构中，在时间步长t时，每个中间神经元接收到一组来自前一时刻的参数(在相同的RNN层中)，两组从前一层RNN隐藏层传递过来的参数；一组来自从左到右的RNN另一组来自从右到左的RNN。

包含L层的深度RNN模型可以用下列式子表示：$$\begin{gathered} {\underset{h}{\to }}_t^{(i)}=f({\underset{W}{\to }}^{(i)}{h}_t^{(i-1)}+{\underset{V}{\to }}^{(i)}{\underset{h}{\to }}_{t-1}^{(i)}+{\underset{b}{\to }}^{(i)}) \\ {\underset{h}{\leftarrow }}_t^{(i)}=f({\underset{W}{\leftarrow }}^{(i)}{h}_t^{(i-1)}+{\underset{V}{\leftarrow }}^{(i)}{\underset{h}{\leftarrow }}_{t+1}^{(i)}+{\underset{b}{\leftarrow }}^{(i)}) \\ \hat{y}=g(U{h}_t+c)=g(U[{\underset{h}{\to }}_t^{(L)};{\underset{h}{\leftarrow }}_t^{(L)}]+c) \end{gathered}$$

应用：RNN翻译模型

本节讨论RNN在翻译方面的应用，以下图所示RNN模型为例：

在这里，德语短语Echt dicke Kiste被翻译成Awesome sauce（图形打印有些纰漏）。前三个隐藏层时间步将德语单词编码为一些语言单词特性(h3)。最后两个时间步将h3解码为英文单词输出。下述式子分别表示了这一编码解码的过程（第一个式子为编码过程，后两个为解码过程）：$$\begin{gathered} h_t=\varphi (h_{t-1},x_t)=f(W^{(hh)}{h}_{t-1}+W^{(hx)}{x}_t) \\ {h}_t=\varphi (h_{t-1})=f(W^{(hh)}{h}_{t-1}) \\ \hat{y}=softmax(W^{(S)}{h}_t) \end{gathered}$$训练过程中使用交叉熵目标函数：$$ma{x}_{\theta }\frac{1}{N}\sum _{n=1}^{N}log{p}_{\theta }(y^{(n)}|x^{(n)})$$在实践中，为了提高模型的翻译精度，需要对模型进行一些扩展：

• 扩展一：训练不同的RNN权值进行编码和解码。这将两个单元解耦，并允许对两个RNN模块进行更精确的预测。意味着编码和解码过程中的 $\varphi ()$ 函数将有不同的$W^{(hh)}$矩阵。
• 扩展二：使用三个不同的输入来计算解码器中的每个隐藏状态（前一个隐藏状态(标准)；编码器的最后一个隐藏层；前一个预测的输出单词）则上述解码器隐藏层计算方法变为：$$h_t=\varphi (h_{t-1},c,y_{t-1})$$
• 扩展三：使用多个RNN层训练深度神经网络。较深的层通常由于其具有较高的学习能力而提高预测精度。同时意味着必须使用大型训练语料库来训练模型。
• 扩展四：训练双向编码器以提高精度。
• 扩展五：给定一个德语单词序列abc，其翻译为英语中的xy，而不是使用abc训练RNN !
  xy，用cb A训练它!
  这种技术背后的直觉是A更有可能被翻译成X。因此，考虑到前面讨论的消失梯度问题，颠倒输入单词的顺序可以帮助降低生成输出短语的错误率。

GRU

除了上述扩展之外，使用更复杂的单元来激活RNN会有更好的表现，比如门控激活函数。
虽然RNN理论上可以捕获长期依赖关系，但实际上很难做到。而门控递归单元具有更持久的内存，从而使RNN更容易捕获长期依赖关系。其数学表达式为：$$\begin{gathered} z_t=\sigma (W^{(z)}{x}_t+U^{(z)}{h}_{t-1}),更新门update \\ {r}_t=\sigma (W^{(r)}{x}_t+U^{(r)}{h}_{t-1}),重置门reset \\ \widetilde{h_t}=tanh(r_t\circ U{h}_{t-1}+W{x}_t),新记忆 \\ {h}_t=(1-z_t)\circ \widetilde{h_t}+z_t\circ h_{t-1}，隐藏单元 \end{gathered}$$上述方程可以认为是GRU的四个基本运算阶段，其中涉及到的参数都使用之前讲解过的反向传播进行学习。整个过程可以用下图进行直观解释：

LSTM

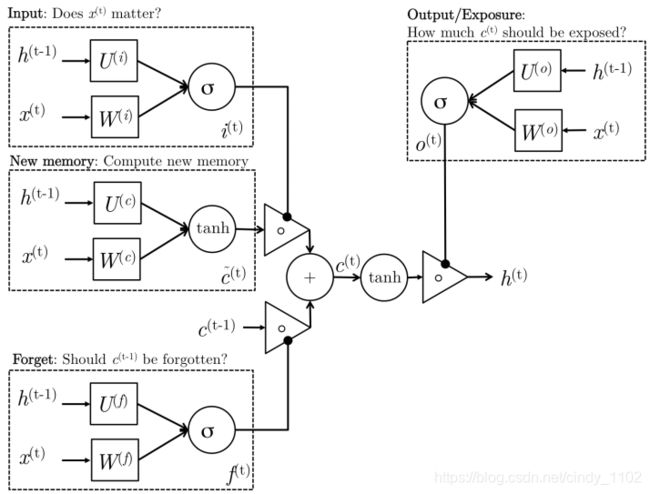
LSTM是另一种复杂的激活单元，与GRU稍有不同。使用这些单元的动机与GRU类似，但是这些单元的体系结构有所不同。同样的，先介绍LSTM单元相关的数学公式：$$\begin{gathered} i_t=\sigma (W^{(i)}{x}_t+U^{(i)}{h}_{t-1}),输入门input \\ {f}_t=\sigma (W^{(f)}{x}_t+U^{(f)}{h}_{t-1}),遗忘门forget \\ {o}_t=\sigma (W^{(o)}{x}_t+U^{(o)}{h}_{t-1}),输出门output \\ \widetilde{c_t}=tanh(W^{(c)}{x}_t+U^{(c)}{h}_{t-1}),新记忆 \\ {c}_t=f_t\circ c_{t-1}+i_t\circ {\tilde{c}}_t,最终记忆 \\ {h}_t=o_t\circ tanh(c_t) \end{gathered}$$整个过程的图形解释如下：