LeetCode 239. 滑动窗口最大值【c++/java详细题解】

1、题目

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例 1：

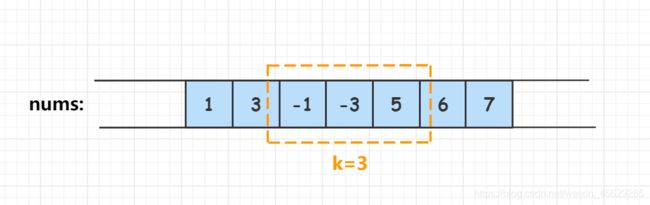
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值

---------------               -----

[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

示例 3：

输入：nums = [1,-1], k = 1
输出：[1,-1]

示例 4：

输入：nums = [9,11], k = 2
输出：[11]

示例 5：

输入：nums = [4,-2], k = 2
输出：[4]

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104
• 1 <= k <= nums.length

2、思路

(单调队列) $O(n)$

首先，我们知道最直接的做法是模拟滑动窗口的过程，每向右滑动一次都遍历一遍窗口内的数字找最大的输出，这样的复杂度是$O(kn)$。考虑优化一下，窗口向右滑动的过程实际上就是将处于窗口的第一个数字删除，同时在窗口的末尾添加一个新的数字，这就可以用双向队列来模拟，每次把尾部的数字弹出，再把新的数字压入到头部，然后找队列中最大的元素即可。

如何快速找出滑动窗口中的最大值？

我们可以在队列中只保留那些可能成为窗口最大元素的数字，去掉那些不可能成为窗口中最大元素的数字。考虑这样一个情况，如果队列中进来一个较大的数字，那么队列中比这个数更小的数字就不可能再成为窗口中最大的元素了，因为这个大的数字是后进来的，一定会比之前早进入窗口的小的数字要晚离开窗口，那么那些早进入且比较小的数字就“永无出头之日”，所以就可以弹出队列。

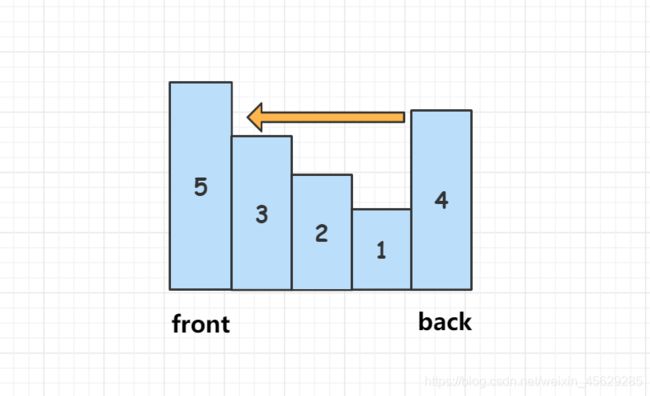
因此队列中的元素就会成保持一个单调递减的顺序，这样我们就维护了一个单调队列。

单调队列

单调队列是一个普通的双端队列，即队头和队尾都可以添加和弹出元素。单调队列顾名思义，队列中元素之间的关系具有单调性，此处的单调性分为单调递增与单调递减。

以单调递减队列为例：

(这里我们规定递减是指从队头到队尾是递减序列）

解题过程如下：

初始时单调队列为空。随着对数组的遍历过程中，每次插入元素前，需要考察两个事情：

• 1、合法性检查：队头下标如果距离i 超过了 k ，则应该出队。
• 2、 单调性维护：如果 nums[i] 大于或等于队尾元素下标所对应的值，则当前队尾再也不可能充当某个滑动窗口的最大值了，故需要队尾出队。始终保持队中元素从队头到队尾单调递减。
• 3、如次遍历一遍数组，队头就是每个滑动窗口的最大值所在下标。

时间复杂度分析： 每个元素最多入队出队一次，复杂度为$O(n)$

3、c++代码

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        deque<int>q; //双端队列
        vector<int>res;
        for(int i = 0; i < nums.size(); i++){
            while(q.size() &&  i - k + 1 > q.front())  q.pop_front(); //判断是否在滑动窗口范围内
            while(q.size() && nums[i] >= nums[q.back()]) q.pop_back();//维护单调递减队列
            q.push_back(i); //将当前元素插入队列
            if(i >= k - 1)  res.push_back(nums[q.front()]); //滑动窗口的元素达到了k个，才可以将其加入答案数组中
        }
        return res;
    }
};

4、java代码

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        Deque<Integer> queue = new ArrayDeque<>(); //双端队列
        int[] res = new int[n - k + 1];
        for (int i = 0 , j = 0; i < n; i++) {
            while (!queue.isEmpty() && i- k + 1 > queue.getFirst())   queue.pollFirst();
            while (!queue.isEmpty() && nums[i] > nums[queue.getLast()])  queue.pollLast();
            queue.offer(i);   
            if( i - k + 1 >= 0) res[j++] = nums[queue.getFirst()];           
        }
        return res;
    }
}

原题链接： 239. 滑动窗口最大值