java数据结构 基本查找,二分查找,分块查找
目录
- 算法查找
-
- 基本查找
- 二分查找
-
- 优化方式 插值查找了解即可
- 斐波那契查找 了解
-
- 以上总结
- 分块查找
算法查找
基本查找
又叫顺序查找 从0索引开始挨个往后查找
需求 定义一个方法利用基本查找 查找某个元素是否存在
{132,135,65,86,89,6}
public static void main(String[] args) {
int arr[]={132,135,65,86,89,6};
int searchNumber=65;
boolean b = basicSearch(arr, searchNumber);
System.out.println(b);
}
private static boolean basicSearch(int arr[], int searchNumber) {
for (int i = 0; i < arr.length; i++) {
if(arr[i]==searchNumber){
return true;
}
}
return false;
}
定义一个方法利用基本查找 查询某个元素在数组中的索引
烤炉数组中元素有重复的可能性
int arr[]={6,135,65,86,89,6} 我要查询6 返回索引为0和5
public static void main(String[] args) {
//定义一个方法利用基本查找 查询某个元素在数组中的索引
//烤炉数组中元素有重复的可能性
//int arr[]={6,135,65,86,89,6} 我要查询6 返回索引为0和5
int arr[]={6,135,65,86,89,6};
int searchNumber=6;
ArrayList<Integer> integers = basicSearch(arr, searchNumber);
for (int i = 0; i < integers.size(); i++) {
Integer integer = integers.get(i);
System.out.println(integer);
}
}
private static ArrayList<Integer> basicSearch(int arr[], int searchNumber) {
ArrayList<Integer>list=new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
if(arr[i]==searchNumber){
list.add(i);
}
}
return list;
二分查找
二分查找1的数组中数据必须是有序的
核心思想:每次排除一半的查找范围
public static void main(String[] args) {
int arr[]={4,23,67,14,126,33};
int number=67;
int i = binarySearch(arr, number);
System.out.println(i);
}
public static int binarySearch(int arr[], int number) {
//定义两个变量记录要查找到范围
int min=0;
int max=arr.length-1;
//2利用循环不断求要找到的数据
while (true){
if(min>max){//如果遇到这个条件相当于循环完了
return -1;
}
//找到 mid位置
int mid=(min+max)/2;
//拿着mid指向元素跟查找的元素比较
if(arr[mid]>number){
//number在mid左边 min不变 max等于mid-1
max=mid-1;
}else if(arr[mid]<number) {
//number在mid又边 max不变 min等于mid+1)
min = mid + 1;
}else{
//number和mid指向元素一样 找到了
return mid;
}
}
}
优化方式 插值查找了解即可
斐波那契查找 了解
以上总结
分块查找
把获得到的数据分成若干个小块
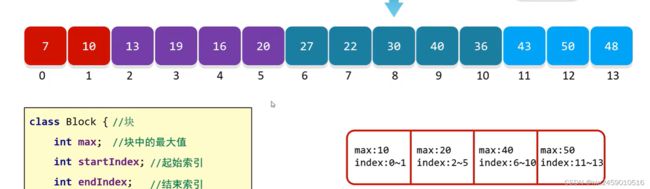
第一块是最小 第一块中最大数据值不会大于第二块所有数据,第二快中最大数据不会大于第三块所有数据…
思路:分成四块每块定义成一个类 类的内容记录了 该块的最大值起始索引和结束索引,然后把这四块对象存在数组内进行调用.如下图
public static void main(String[] args) {
int arr[]={16,5,9,12,21,18,
32,23,37,26,45,34,
50,48,61,52,73,66};
//分成了三块.分块思路总数开根号 这个是16个 开根号等于4.5左右
//定义一个类存储三个组
Block b1=new Block(21,0,5);
Block b2=new Block(45,6,11);
Block b3=new Block(73,12,17);
//定义一个数组存储管理上面三个组(索引表)
Block[]blockarr={b1,b2,b3};
int number=37;
//要查询的数
//调用方法传递索引表 要查询的数据 arr数组
int index = getIndex(blockarr, arr, number);
System.out.println(index);
}
private static int getIndex(Block[] blockarr, int[] arr, int number) {
//在这之前要知道要查询的数number在哪个组里
//定义一个方法
int numberIndex = getNumberIndex(blockarr, number);
//numberIndex就是找到的符合的组块索引
//获取这块索引得最大值 起始索引和结束
int endIndex = blockarr[numberIndex].getEndIndex();
int maxIndex = blockarr[numberIndex].getMaxIndex();
int startIndex = blockarr[numberIndex].getStartIndex();
//遍历该组
for (int i = startIndex; i < endIndex; i++) {
if(arr[i]==number){
return i;
}
}
return -1;
}
private static int getNumberIndex(Block[] blockarr, int number) {
for (int i = 0; i < blockarr.length; i++) {
//思路 获取每个组中最大数 找到比要查询的数小的哪个就是
if(blockarr[i].getMaxIndex()>number){
return i;
}
}
return -1;//找不到直接返会-1结束代码
}
}
class Block{
private int maxIndex;
private int startIndex;
private int endIndex;
public Block() {
}
public Block(int maxIndex, int startIndex, int endIndex) {
this.maxIndex = maxIndex;
this.startIndex = startIndex;
this.endIndex = endIndex;
}
/**
* 获取
* @return maxIndex
*/
public int getMaxIndex() {
return maxIndex;
}
/**
* 设置
* @param maxIndex
*/
public void setMaxIndex(int maxIndex) {
this.maxIndex = maxIndex;
}
/**
* 获取
* @return startIndex
*/
public int getStartIndex() {
return startIndex;
}
/**
* 设置
* @param startIndex
*/
public void setStartIndex(int startIndex) {
this.startIndex = startIndex;
}
/**
* 获取
* @return endIndex
*/
public int getEndIndex() {
return endIndex;
}
/**
* 设置
* @param endIndex
*/
public void setEndIndex(int endIndex) {
this.endIndex = endIndex;
}
public String toString() {
return "Block{maxIndex = " + maxIndex + ", startIndex = " + startIndex + ", endIndex = " + endIndex + "}";
}
}





