Gold序列

文章目录

前言

一、Gold序列产生原理

1.1 m序列

1.2 Gold序列

二、仿真实验

总结

---

前言

         本文主要介绍Gold序列的产生以及相关性仿真。

---

一、Gold序列产生原理

1.1 m序列

• m序列产生

       m序列是最大长度线性移位寄存器序列的简称，是由多级移位寄存器或其他延迟元件通过线性反馈产生的最长的码序列。若r为级数，所能产生的最大长度的码序列为n=2^r-1位。

       m序列的生成是由反馈电路以及初始状态决定，且由反馈逻辑电路决定的特征多项式必须是r级的本原多项式，初始状态不能全是0，此时初始状态将决定m序列的初始相位，本原多项式决定m序列的形状。

       若r级线性移位寄存器的初始状态为：，且满足线性反馈逻辑如下:

     则对应的特征多项式可表示为：，若记

进一步有：，由此可得特定本原多项式以及非全零初始状态下，移位寄存器生成的m序列。

m序列的自相关性

      m序列的自相关函数是双值函数，归一化自相关函数满足：

           

       m序列虽然有良好的自相关性以及互相关性，但m序列可供选择的地址码数量少，为解决这一问题，需要引入组合码，而Gold序列就是组合码中重要的一类。

1.2 Gold序列

m序列优选对

       两个m序列，例如a和b是同级但不同的本原多项式所产生的m序列对，则构成优选对的条件是，其互相关函数值满足下式：

       

下面是几种不同级数的m序列优选对允许的最大相关函数值

Gold序列产生

       Gold码序列是由m序列优选对模2相加构成的，并且每改变一个m序列的相对位移，就可以得到一个新的Gold序列。这样每组m序列优选对可以产生2^r+1个Gold序列。

Gold序列的相关特性

        Gold码组的互相关函数值不会超过原两m序列间的最大互相关函数值，若c,d为m序列优选对a,b构成的Gold序列，则：

二、仿真实验

      特征多项式，都是本原多项式，这两个本原多项式对应着两个不同的m序列，初始状态都为[1 0 0 ...0]证明这对m序列是优选对，画出他们以及由他们生成的Gold 序列的自相关图像和互相关图像。

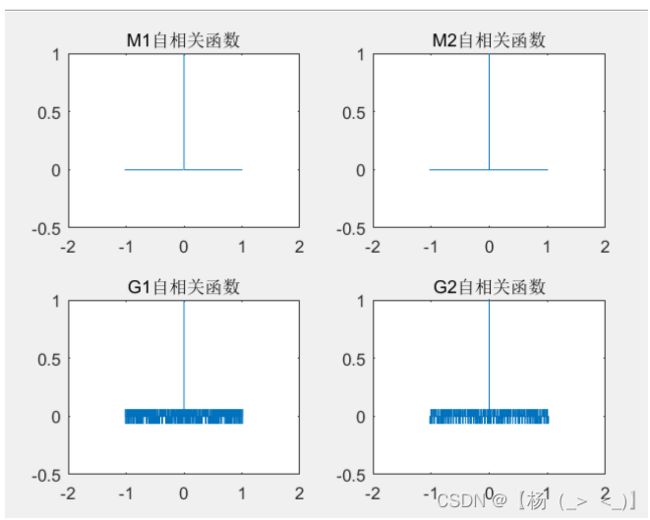
m序列，Gold序列的自相关函数

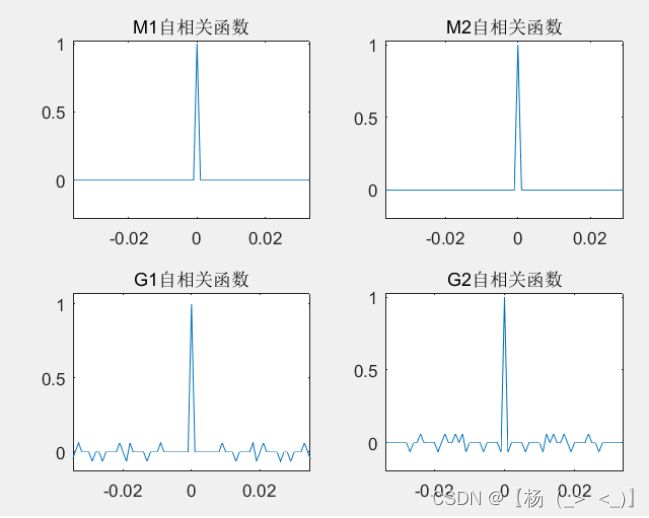
m序列，Gold序列的自相关函数局部放大图

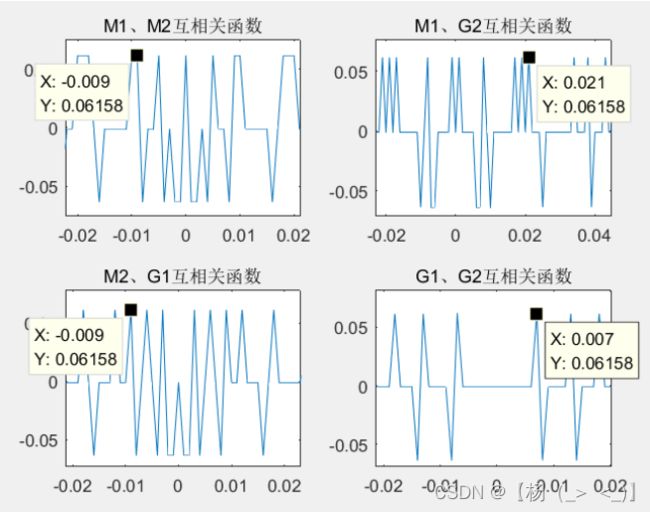
 m序列，Gold序列的互相关函数

m序列，Gold序列的互相关函数局部放大图

       由结果可知：由本原多项式，生成的m序列对之间的互相关函数最大值为0.06158小于65/1023（0.0635），所以该m序列对是优选对，且由m序列优选对产生的Gold序列的互相关函数最大值也小于65/1023。

        可以看出生成的m序列以及Gold序列具有良好的自相关特性以及互相关特性，且通过改变m序列的位移相位可以得到2^r+1个不同的Gold序列。

代码

%**************************************************
%m序列，Gold序列的自相关函数、互相关函数
%**************************************************
clear all;
%**************************************************
%寄存器参数
%**************************************************
T=1e-3;                           %码片宽度
r=10;                             %寄存器位数
n=2^r-1;                          %m序列长度
M1=zeros(1,n);
M2=zeros(1,n);
M1(1)=1;                          %初始状态10000000000
M2(1)=1;
f1=[1 0 0 0 0 0 0 1 0 0 1];       %特征多项式x^10+x^3+1对应的系数
f2=[1 0 1 0 0 0 0 1 1 0 1];       %特征多项式x^10+x^8+x^3+x^2+1对应的系数
%***************************************************
%产生m序列
%***************************************************
for i=r+1:n;                      %递推公式得到m序列
    M1(i)=mod(sum(M1(i-r:i-1).*f1(1:r)),2);
    M2(i)=mod(sum(M2(i-r:i-1).*f2(1:r)),2);
end
% ***************************************************
% 产生Gold序列
% ***************************************************
G1=mod(M1+M2,2);                  %0比特相位差
s=102;                              %s在0-n之间
G2=mod(M1+[M2(s+1:n) M2(1:s)],2); %s比特相位差
%***************************************************
%双极性序列
%***************************************************
M1=2*M1-1;                        %双极性m序列
M2=2*M2-1;                        %双极性m序列
G1=2*G1-1;                        %双极性m序列
G2=2*G2-1;                        %双极性m序列
%***************************************************
%自相关函数
%***************************************************
N=2*n-1;
t=(-n+1:n-1)*T;
Rm1=zeros(1,N);                  %M1的自相关函数
Rm2=zeros(1,N);                  %M2的自相关函数
Rg1=zeros(1,N);                  %G1的自相关函数
Rg2=zeros(1,N);                  %G2的自相关函数
 
for j=0:n-1
Rm1(n+j)= sum(M1.*[M1(j+1:n) M1(1:j)])/n;
Rm2(n+j)= sum(M2.*[M2(j+1:n) M2(1:j)])/n;
Rg1(n+j)= sum(G1.*[G1(j+1:n) G1(1:j)])/n;
Rg2(n+j)= sum(G2.*[G2(j+1:n) G2(1:j)])/n;
end
Rm1(1:n-1)= Rm1(N:-1:n+1);
Rm2(1:n-1)= Rm2(N:-1:n+1);
Rg1(1:n-1)= Rg1(N:-1:n+1);
Rg2(1:n-1)= Rg2(N:-1:n+1);
figure(1)
subplot(221);
plot(t,Rm1);
title('M1自相关函数');
subplot(222);
plot(t,Rm2);
title('M2自相关函数');
subplot(223);
plot(t,Rg1);
title('G1自相关函数');
subplot(224);
plot(t,Rg2);
title('G2自相关函数');
%********************************************************
%互相关函数
%********************************************************
Rm1m2=zeros(1,N);
Rm1g2=zeros(1,N);
Rm2g1=zeros(1,N);
Rg1g2=zeros(1,N);
 
for j=0:n-1
Rm1m2(n+j)= sum(M1.*[M2(j+1:n) M2(1:j)])/n;
Rm1g2(n+j)= sum(M1.*[G2(j+1:n) G2(1:j)])/n;
Rm2g1(n+j)= sum(M2.*[G1(j+1:n) G1(1:j)])/n;
Rg1g2(n+j)= sum(G1.*[G2(j+1:n) G2(1:j)])/n;
end
Rm1m2(1:n-1)= Rm1m2(N:-1:n+1);
Rm1g2(1:n-1)= Rm1g2(N:-1:n+1);
Rm2g1(1:n-1)= Rm2g1(N:-1:n+1);
Rg1g2(1:n-1)= Rg1g2(N:-1:n+1);
figure(2)
subplot(221);
plot(t,Rm1m2);
title('M1、M2互相关函数');
subplot(222);
plot(t,Rm1g2);
title('M1、G2互相关函数');
subplot(223);
plot(t,Rm2g1);
title('M2、G1互相关函数');
subplot(224);
plot(t,Rg1g2);
title('G1、G2互相关函数');

---

总结

       转载请附链接：【杨（_> <_)】的博客_CSDN博客-信号处理,代码实现,SAR领域博主