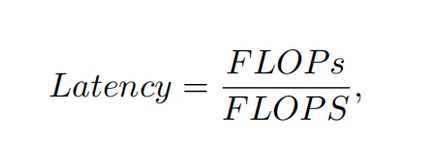FatesrNet：Run, Don‘t Walk: Chasing Higher FLOPS for Faster Neural Networks

        概述：为了实现更快的网络，作者重新回顾了FLOPs的运算符，并证明了如此低的FLOPS主要是由于运算符的频繁内存访问，尤其是深度卷积。因此，作者提出了一种新的partial convolution（PConv），通过同时减少冗余计算和内存访问可以更有效地提取空间特征，又基于PConv进一步提出FasterNet框架。

---

1.背景

        计算机视觉任务追求具有低延迟和高吞吐量的快速神经网络，研究人员设计具有成本效益的快速神经网络，降低计算复杂度，主要以浮点运算（FLOPs）的数量来衡量。

2.问题

        CNN:

        MobileNet、ShuffleNet和GhostNet等利用深度卷积（DWConv）和/或组卷积（GConv）来提取空间特征。然而，在减少FLOPs的过程中，算子经常会受到内存访问增加的副作用的影响。MicroNet进一步分解和稀疏网络，将其FLOPs推至极低水平。尽管这种方法在FLOPs方面有所改进，但其碎片计算效率很低。此外，上述网络通常伴随着额外的数据操作，如级联、Shuffle和池化，这些操作的运行时间对于小型模型来说往往很重要。

        VIT：

        除了上述纯卷积神经网络（CNNs）之外，人们对使视觉Transformer（ViTs）和多层感知器（MLP）架构更小更快也越来越感兴趣。例如，MobileViT和MobileFormer通过将DWConv与改进的注意力机制相结合，降低了计算复杂性。然而，它们仍然受到DWConv的上述问题的困扰，并且还需要修改的注意力机制的专用硬件支持。使用先进但耗时的标准化和激活层也可能限制其在设备上的速度。

        这些“快速”的神经网络真的很快吗？

        作者检查了延迟和FLOPs之间的关系：许多现有神经网络的FLOPS较低，其FLOPS通常低于流行的ResNet50。由于FLOPS如此之低，这些“快速”的神经网络实际上不够快。它们的FLOPs减少不能转化为延迟的确切减少量。

3方法

        作者重新审视了现有的操作符，特别是DWConv的计算速度——FLOPS。作者发现导致低FLOPS问题的主要原因是频繁的内存访问。然后，作者提出了PConv作为一种竞争性替代方案，它减少了计算冗余以及内存访问的数量。

4.步骤

PConv：

原理：

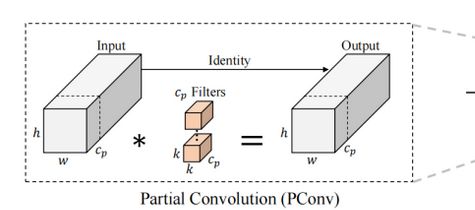
         PConv：它利用了特征图中的冗余，并系统地仅在一部分输入通道上应用规则卷积（Conv），而不影响其余通道。本质上，PConv的FLOPs低于常规Conv，而FLOPs高于DWConv/GConv

        常规卷积：

        DW卷积：

        减少了FLOPS，但精度严重下降，

工作原理

         它只需在输入通道的一部分上应用常规Conv进行空间特征提取，并保持其余通道不变。对于连续或规则的内存访问，将第一个或最后一个连续的通道cp视为整个特征图的代表进行计算。在不丧失一般性的情况下认为输入和输出特征图具有相同数量的通道。因此，PConv的FLOPs仅为：

PConv之后是PWConv      

        为了充分有效地利用来自所有通道的信息，进一步将逐点卷积（PWConv）附加到PConv。它们在输入特征图上的有效感受野看起来像一个T形Conv，与均匀处理补丁的常规Conv相比，它更专注于中心位置。

 FasterNet：

  

        每个层次级前面都有一个嵌入层（步长为4的常规4×4卷积）或一个合并层（步长为2的常规2×2卷积），用于空间下采样和通道数量扩展

        每个FasterNet块有一个PConv层，后跟2个PWConv（或Conv 1×1）层。它们一起显示为倒置残差块，其中中间层具有扩展的通道数量，并且放置了Shorcut以重用输入特征。（PConv+2个1*1的Conv或2个PWConv+BN+Relu激活函数）

        除了上述算子，标准化和激活层对于高性能神经网络也是不可或缺的。然而，许多先前的工作在整个网络中过度使用这些层，这可能会限制特征多样性，从而损害性能。它还可以降低整体计算速度。相比之下，只将它们放在每个中间PWConv之后，以保持特征多样性并实现较低的延迟。

1.         此外，使用批次归一化（BN）代替其他替代方法。BN的优点是，它可以合并到其相邻的Conv层中，以便更快地进行推断，同时与其他层一样有效。对于激活层，根据经验选择了GELU用于较小的FasterNet变体，而ReLU用于较大的FasterNet变体，同时考虑了运行时间和有效性。最后三个层，即全局平均池化、卷积1×1和全连接层，一起用于特征转换和分类。

---

知识点

        1.FLOPS(S大写)：floating-point operations per second的缩写，意指每秒浮点运算次数。用来衡量硬件的性能。

        2.FLOPs(S小写)：floating-point of operations的缩写，是浮点运算次数，可以用来衡量算法/模型复杂度

        3.GFLOPS：Giga Floating-point Operations Per Second,即每秒10亿次的浮点运算数,常作为GPU性能参数但不一定代表GPU的实际表现，因为还要考虑具体如何拆分多边形和像素、以及纹理填充，理论上该数值越高越好。1GFlops = 1,000MFlops

        4.Embedding(嵌入层，文中用于空间下采样)：在目标检测中，通常使用卷积神经网络（CNN）作为特征提取器。嵌入层可以在CNN的顶部添加，将CNN的输出特征图（通常是一个高维张量）转换为一个向量。它的作用是将高维离散输入转换为低维连续向量表示。具体来说，嵌入层将每个输入元素表示为一个向量，这个向量的维度通常要比输入元素的个数小得多。这样做的好处是可以减少网络中的参数量，提高训练效率，并且可以让网络更好地表达输入元素之间的相似性关系。

        5.Merging（合并层，文中用于通道数量扩展）：主要作用是将多个输入层或多个中间层的数据合并在一起。这个过程通常是通过对输入层或中间层的数据进行某种形式的操作来实现的，例如连接、叠加、求和等。

        6.常见激活函数优缺点

        6.1 sigmoid函数

        优点：输出值在0到1之间，可以将输出解释为概率。

        缺点：当输入值趋近于正无穷或负无穷时，梯度值会趋近于0，导致梯度消失问题，使得深度神经网络的训练变得困难。

        6.2 tanh函数

        优点：它的输出值在-1到1之间，比sigmoid函数的输出范围更大，可以提供更多的非线性   

        缺点：与sigmoid函数相同，当输入值趋近于正无穷或负无穷时，梯度消失问题仍然存在

        6.3 ReLU函数

        优点：它可以有效地避免梯度消失问题，加速神经网络的训练

        缺点：它在输入为负数时，梯度为0，会使得一部分神经元永久失活，称为“ReLU死亡问题”。

        6.4 Leaky ReLU函数：Leaky ReLU函数是对ReLU函数的改进

        优点：可以避免ReLU死亡问题，同时仍然保持了ReLU函数的优点

        缺点：它在输入为负数时，仍然存在梯度消失问题

        6.5 ELU函数：ELU函数是另一种改进ReLU函数的激活函数

        优点：它可以避免ReLU死亡问题和梯度消失问题，同时仍然保持了ReLU函数的优点。

        缺点：它比其他激活函数计算量大，训练时间长。

        6.6 Gelu函数

        优点：激活函数的值域在整个实数范围内，避免了sigmoid函数在极端值处的梯度消失问题； 激活函数的导数在大部分区间内都为非零值，避免了ReLU函数在负数区间内的梯度为0问题；Gelu函数在接近0时的导数接近1，能够保留更多的信息。

         缺点：Gelu函数的计算比ReLU函数复杂，计算速度较慢；Gelu函数在负数区间内仍然存在梯度消失问题。 

        6.7 Silu函数

        优点：计算速度比ReLU函数更快，因为它只涉及一个sigmoid函数的计算；Silu函数在接近0时的导数接近1，能够保留更多的信息。

        Silu的缺点：Silu函数在接近正无穷和负无穷时的导数接近0，可能导致梯度消失问题；Silu函数的值域在(0,1)之间，可能会导致信息的损失。

        7.

---

参考：

CVPR2023最新Backbone |FasterNet远超ShuffleNet、MobileNet、MobileViT等模型