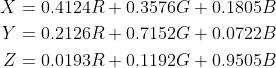Gamma-Correct Rendering(翻译)
随着消费类硬件能够渲染渲染高动态范围图像数据，(进入)8位sRGB帧缓冲区的时代越来越近了。下一代图形设备的编程人员能够对照明系统进行高精度建模，然后将这些值映射到常规8位sRGB设备（例如PC显示器）的可显示范围内。[注：原文写于2004年，年代久远，开场白看看就好。]
从源图像到最终输出图形的转换过程非常复杂，并且需要程序员在不同的颜色空间中处理。在这篇文章中，我将会简要介绍颜色空间，然后详细介绍转换过程中一个通常被忽略但依然很重要的地方，那就是gamma函数。
sRGB标准
sRGB的色彩空间是根据昏暗环境工作条件下办公室的显示器特性而设计的，并已由IEC (IEC 61966-1-2)标准化。该色彩空间已被业界广泛采用，广泛应用于CRT、LCD、投影仪等领域。现代8位图像文件格式(如jpeg2000或PNG)默认为sRGB颜色空间。
sRGB颜色空间中的值是一个浮点三元数组，每个值在0.0到1.0之间。 超出此范围的值将被裁剪。这些sRGB颜色值通常会被编码为0到255之间的8位无符号整数。
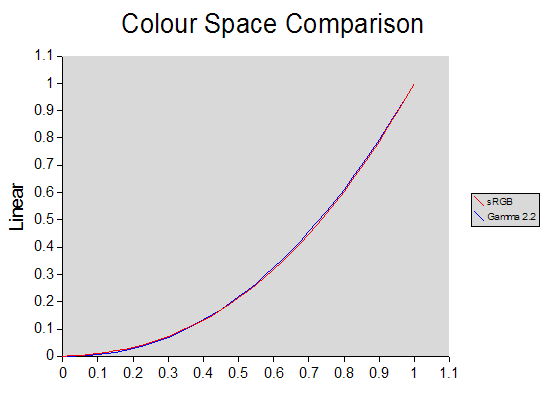
关于sRGB，关键要记住它是非线性的。 它大致遵循曲线 y = x ^2.2 ，实际的标准曲线稍微复杂一些。 sRGB与gamma 2.2的关系图如下所示：
颜色空间对比
此映射具有很好的特性，低亮度RGB值具有更高的分辨率，非常适合人类的视觉模型。
Gamma函数作为近似值
从上图可以看出，sRGB标准非常接近Gamma2.2曲线。 因此，完整的sRGB转换功能通常用更简单的Gamma函数来近似。
请注意，与单词Gamma关联的值是函数y = x ^ p 中使用的幂值。 不幸的是，Gamma通常与亮度有关，而Gamma与亮度并不完全相同。完整的0-1区间始终映射回完整的0-1区间 [注：这里的意思可能是把[0,255]映射回[0,1]]。
这个颜色空间用到了什么样的数学?
通常，你的照明处理过程应在线性空间中进行，以便所有照明都是线性累积的。这是许多下一代引擎中采用的方法，也是确保你的物理正确性的唯一方法。
但是，假设Gamma函数近似值足够好，你仍然可以执行调整操作。 在这种情况下，我们有一些常数A，希望使用它来调整sRGB源数据x，并将结果存储在sRGB中作为y。 在线性空间中，可以这样写：
![y ^{2.2}=Ax^{2.2}=\left [ A^{\frac{1}{2.2}}x \right ]^{2.2}](http://img.e-com-net.com/image/info8/fab0a7fb30e343fc930c6372a5d61db8.gif){kind=small}
由于我们只在0-1区间内工作，所以我们可以在sRGB工作空间内把两边的指数约掉。得到:
因此，如果我们将常量转换进sRGB，调整运算依然可行。 但是，只有极少数的运算可以用这种方式进行。加法运算（用于加法照明模型或用于alpha混合）不能为工作在gamma 2.2空间而重新制定，因为这个空间是非线性的。如果你希望有一个正确的可加照明模型，则必须在线性空间中工作，这意味着你需要一个高精度的帧缓冲区以至少匹配sRGB的低亮度粒度。
一个sRGB示例:Mip映射
如果在sRGB颜色空间中对图像进行双线性过滤，则最终总是会得到比正确结果更暗的过滤颜色。错误量随着输入颜色范围的增加而增加。这是黑白网格经过过滤且不进行颜色空间转换的最坏情况的示例：
中心图像包含交替的黑白线。 左图像和右图像是通过对图像进行降采样，然后按比例放大回原始大小而生成的。 左图是在线性空间中进行降采样，右图是直接在sRGB中进行降采样。
在标准照明条件下经过正确校准的监视器上，左侧图像和中央图像应显示相同的整体亮度。 这是因为线性空间平均值为50％灰色，它在sRGB中被映射为186的值。 右侧图像的sRGB值为128，但是在线性空间中只有21.4％的灰色，因此应显得更暗。
大多数游戏材质的亮度变化都没有那么高，因此直接过滤sRGB颜色引入的错误远没有本示例中那么严重。 但是，在将每个Mip级别保存到sRGB中之前，应将任何高变化数据（例如预先计算的光照贴图）过滤为线性光照值。
总结
当代的图形硬件可以在材质读取指令期间将数据从sRGB移动到线性空间，并且假设你使用了高精度的帧缓冲区，那么将最终的渲染转换回sRGB以在显示设备上使用的成本很低。 在工具中，我们将更多的精力放在正确性上，因此可以忽略在色彩空间之间移动所需的额外转换时间。
期望下一代渲染引擎能够正确模拟复杂照明方程式的所有微妙之处，因此在整个艺术流程和渲染系统中必须对色彩空间有所了解是至关重要的。 希望本文让大家了解了色彩空间非常重要的区域。下一部分包含了我在美术工具和渲染代码中都使用过的一些转换方程式。
相关公式
sRGB to linear RGB: rgb (sRGB), RGB (linear RGB)
一般而言，上式近似地作为计算
linear RGB to sRGB: RGB (linear RGB), rgb (sRGB)
一般而言，上式近似地作为计算
XYZ to linear RGB: (D65 white point)
linear RGB to XYZ: (D65 white point)
[注：这里的D65是指CIE标准光源]