【C++】二叉树题目总结
文章目录
- 一. 前序遍历类
-
- 1、二叉树的前序遍历(非递归)
- 2、根据二叉树创建字符串
- 3、树的子结构
- 4、二叉树的镜像
- 二. 中序遍历类
-
- 1、二叉树的中序遍历(非递归)
- 三. 后序遍历类
-
- 1、二叉树的后序遍历(非递归)
- 2、平衡二叉树
- 四. 层序遍历类
-
- 1、二叉树的层序遍历
- 五. 搜索树类题目
-
- 1、二叉搜索树与双向链表
- 2、将有序数组转换为二叉搜索树
- 3、二叉搜索树的第k大节点
- 六. 其他类型题目
-
- 1、Pre-Post
- 2、二叉树的最近公共祖先
一. 前序遍历类
1、二叉树的前序遍历(非递归)
题目连接
题目描述:
给你二叉树的根节点 root ,返回它节点值的前序遍历。
解题思路:
前序遍历的访问顺序是:根节点 -> 左子树 -> 右子树。
具体操作方法:从根节点开始用一个栈存储根和它的左路节点,并依次把节点的val放入结果数组中。放完后我们取出栈顶元素,对于该节而言它本身和它的左路节点都已经访问过了,接下来循环回去访问它的右子树,重复这个过程完成整棵树的前序遍历。
完整代码:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
// 遍历以cur为根的树
while(cur || !st.empty())
{
// 1、先把根及其左路节点访问了并且放入栈中
while(cur)
{
ret.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
// 2、拿出栈顶的节点,该节点及其它的左子树都已经被访问过
// 接下来只需访问它的右子树即可
cur = st.top()->right;
st.pop();
}
return ret;
}
};
性能分析:
- 时间复杂度:O(n)。每个节点都要入栈、出栈一次。
- 空间复杂度:O(n)。单支树时,所有节点同时都要入栈。
2、根据二叉树创建字符串
题目连接
题目描述:
你需要采用前序遍历的方式,将一个二叉树转换成一个由括号和整数组成的字符串。
空节点则用一对空括号 “()” 表示。而且你需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

解题思路:
对照示例的输入输出来理解题目,按照前序遍历的顺序先处理根节点,如果存在左子树就处理左子树,然后右子树;如果不存在左子树但有右子树,在处理右子树之前要先加上一个空括号对来标志仅存在右子树。
可以使用 to_string 来把节点的val转化成字符串。
完整代码:
class Solution {
public:
string tree2str(TreeNode* root)
{
string s;
// 根节点为空的话返回空字符串
if(!root)
{
return s;
}
// 1、先处理根节点
s += to_string(root->val);
// 2、再处理左子树
if(root->left)
{
s += '(';
s += tree2str(root->left);
s += ')';
}
// 3、最后处理右子树
if(root->right)
{
// 注意:如果左子树为空的话,处理前要在前面加上一对空括号来标志后面的是右子树
if(root->left == nullptr)
{
s += "()";
}
s += '(';
s += tree2str(root->right);
s += ')';
}
// 4、返回最终结果
return s;
}
};
性能分析:
- 时间复杂度:O(n)。其中n是二叉树中的节点数目。
- 空间复杂度:O(n)。每个节点的处理都需要开辟一个栈帧。
3、树的子结构
题目连接
题目描述:
输入两棵二叉树A,B,判断B是不是A的子结构。(我们约定空树不是任意一个树的子结构)
解题思路:
前序方式遍历A树的每一个节点,让以这些节点为根的子树去跟B树比较,判断B树是否是它们的子树。
完整代码:
class Solution
{
public:
bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
{
// 空树不是任何一棵树的子树
if(!pRoot1 || !pRoot2)
{
return false;
}
// 当前节点的子树? || 左子树的子树? || 右子树的子树?
return _HasSubtree(pRoot1, pRoot2) || HasSubtree(pRoot1->left, pRoot2) || HasSubtree(pRoot1->right, pRoot2);
}
private:
bool _HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
{
// 当pRoot2等于空时,确定是它是子树
if(pRoot2 == nullptr)
{
return true;
}
// 至此pRoot2肯定不为空:当pRoot1不存在或两个节点的val不同,说明pRoot2肯定不是子树
if(pRoot1 == nullptr || pRoot1->val != pRoot2->val)
{
return false;
}
// 继续看其余的节点是否相同
return _HasSubtree(pRoot1->left, pRoot2->left) && _HasSubtree(pRoot1->right, pRoot2->right);
}
};
性能分析:
- 时间复杂度:O(n)。当两棵树一模一样时,需要遍历它们的所有节点。
- 空间复杂度:O(n)。
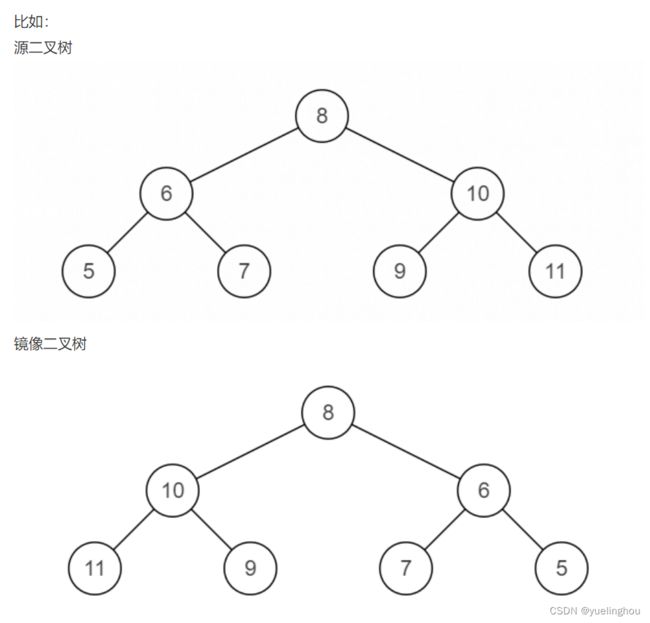
4、二叉树的镜像
题目连接
题目描述:
操作给定的二叉树,将其变换为源二叉树的镜像。
数据范围:二叉树的节点数 0 <= n <= 1000, 二叉树每个节点的值 0 <= val <= 1000
解题思路:
二叉树的镜像就是每一个节点的左右孩子对调,我们利用前序遍历拿到原二叉树的每一个节点,利用std::swap(...)去交换节点的左右孩子即可完成镜像。
完整代码:
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pRoot TreeNode类
* @return TreeNode类
*/
TreeNode* Mirror(TreeNode* pRoot)
{
// 根节点为空没必要镜像了
if(pRoot == nullptr)
{
return pRoot;
}
// 1、根节点的左右孩子
std::swap(pRoot->left, pRoot->right);
// 2、让左子树镜像
Mirror(pRoot->left);
// 3、让右子树镜像
Mirror(pRoot->right);
// 4、返回根节点
return pRoot;
}
};
性能分析:
- 时间复杂度:O(n)。
- 空间复杂度:O(n).
二. 中序遍历类
1、二叉树的中序遍历(非递归)
题目描述:
给定一个二叉树的根节点 root ,返回它的中序遍历。

解题思路:
中序遍历顺序:左子树 -> 根节点 -> 右子树。
先把根节点及其它的左路节点都入栈,接下来取栈顶节点,该节点的特征是:左子树已经遍历完成,把该节点的val加入结果数组中,然后右子树重复上面的过程,最后中序遍历完整棵树。
完整代码:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root)
{
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
// cur是谁就遍历那棵树
while(cur || !st.empty())
{
// 1、先把根节点及其它的左路节点入栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
// 2、拿出的栈顶节点左子树已经访问完成,接下来访问它自己及其它的右子树
TreeNode* top = st.top();
st.pop();
ret.push_back(top->val);
cur = top->right;
}
return ret;
}
};
性能分析:
- 时间复杂度:O(n)。每个节点都要入栈、出栈一次。
- 空间复杂度:O(n)。单支树时,所有节点同时都要入栈。
三. 后序遍历类
1、二叉树的后序遍历(非递归)
题目连接
题目描述:
给定一个二叉树,返回它的后序遍历。

解题思路:
先把根节点及其它的左路节点都入栈,接下来取栈顶节点,该节点的特征是:左子树已经遍历完成。这个节点能否加入结果数组取决于它的右子树是否遍历完成,如果没有的话,需要先遍历它的右子树。
完整代码:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root)
{
vector<int> ret;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* prev = nullptr;
while(cur || !st.empty())
{
// 1、先把根节点及其左路节点入栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
// 2、拿出栈顶节点,该节点的左子树已经处理完成
// 如果该节点的右孩子为空或者右子树已经访问完成,该节点才能访问
TreeNode* top = st.top();
if(top->right == nullptr || top->right == prev)
{
// 经过第一步的处理cur一定为空
// 所以这里面不用管cur
st.pop();
ret.push_back(top->val);
prev = top;
}
else
{
cur = top->right;
}
}
return ret;
}
};
性能分析:
- 时间复杂度:O(n)。每个节点都要入栈、出栈一次。
- 空间复杂度:O(n)。单叉树时,所以节点都要同时入栈。
2、平衡二叉树
题目连接
解题思路:后序遍历二叉树,并把当前树的高度反馈给它的父亲节点。
完整代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution
{
private:
bool _isBalanced(TreeNode* root, int& high)
{
if(root == nullptr)
{
return true;
}
int leftHigh=0;
int rightHigh=0;
bool bLeft=_isBalanced(root->left, leftHigh);
bool bRight=_isBalanced(root->right, rightHigh);
high=max(leftHigh, rightHigh)+1;// 更新给父亲节点该树的高度
return bLeft && bRight && abs(leftHigh - rightHigh)<2;// 返回给父亲节点,该树是否是平衡树
}
public:
bool isBalanced(TreeNode* root)
{
// 1、根节点为空也算平衡树
if(root == nullptr)
{
return true;
}
// 2、根节点不为空,后序遍历二叉树,并记录左右子树的高度
int leftHigh=0;
int rightHigh=0;
return _isBalanced(root->left, leftHigh)
&& _isBalanced(root->right, rightHigh)
&& abs(leftHigh - rightHigh)<2;
}
};
性能分析:
- 时间复杂度:O(N)。
- 空间复杂度:O(N)。
四. 层序遍历类
1、二叉树的层序遍历
题目连接
题目描述:
给你一个二叉树,请你返回其按层序遍历得到的节点值。(即逐层地,从左到右访问所有节点)。

解题思路:
借助队列拿出每一层节点的同时按照从左到右的顺序存入下一层的所有节点,其核心代码下面这条,确保拿出当前层的节点:
for(size_t i = q.size(); i > 0; --i)
完整代码:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
// 1、如果根节点为空的话,返回一个空的二维数组
if(!root)
{
return vector<vector<int>>();
}
// 2、创建相关数据结构
queue<TreeNode*> q;
vector<vector<int>> vv;
// 3、借助队列搜索二叉树的每一层节点
q.push(root);
while(!q.empty())
{
vector<int> v;
for(size_t i = q.size(); i > 0; --i)
{
TreeNode* front = q.front();
q.pop();
v.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
}
return vv;
}
};
性能分析:
- 时间复杂度:O(n)。需要遍历每一个节点。
- 空间复杂度:O(n)。队列的开销。总节点个数2^h - 1,最后一层节点个数为2^(h-1),最后一层节点个数相当于总节点个数的一半,即n/2,所以空间复杂度渐进表示为O(n)。
五. 搜索树类题目
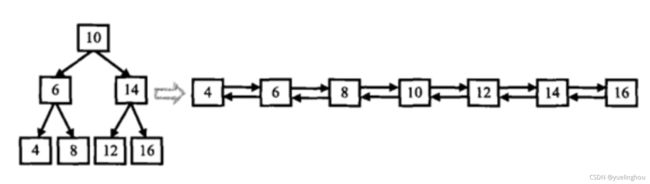
1、二叉搜索树与双向链表
题目连接
题目描述:
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示:
数据范围:输入二叉树的节点数 0 \le n \le 10000≤n≤1000,二叉树中每个节点的值 0\le val \le 10000≤val≤1000
要求:空间复杂度O(1)O(1)(即在原树上操作),时间复杂度 O(n)O(n)
注意:
- 要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
- 返回链表中的第一个节点的指针
- 函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构
- 你不用输出双向链表,程序会根据你的返回值自动打印输出
输入描述:
二叉树的根节点
返回值描述:
双向链表的其中一个头节点。
示例1:
输入:
{10,6,14,4,8,12,16}
返回值:
From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;
说明:
输入题面图中二叉树,输出的时候将双向链表的头节点返回即可。
示例2:
输入:
{5,4,#,3,#,2,#,1}
返回值:
From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;
说明:
5
/
4
/
3
/
2
/
1
树的形状如上图 (单叉树,只有左分支)
解题思路:
题目要求将二叉搜索树转化成一个排序的双向链表,对于搜索树而言它的中序遍历是有序序列,我们考虑在中序遍历的过程中完成树到双向链表的转化。
传统的中序遍历过程中每次只能拿到一个节点。

想要转化成双向链表必须两两建立联系,考虑每次还能够传入当前节点的前一个节点prev,这样在每一次递归调用中:
完整代码:
class Solution
{
private:
void InOrder(TreeNode* cur, TreeNode*& prev)
{
// 如果当前节点为空,不用处理
if(!cur)
{
return;
}
// 1、先处理左子树
InOrder(cur->left, prev);
// 2、处理上一个节点的后继和当前节点的前驱
// 此时当前节点的right还没处理,可以递归到右子树,到右子树中把当前节点作为prev完成后继的处理
if(prev)
{
prev->right = cur;
}
cur->left = prev;
prev = cur;
// 3、最后处理右子树
InOrder(cur->right, prev);
}
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
// 1、空树的话返回空指针回去就行
if(!pRootOfTree)
{
return nullptr;
}
// 2、在InOrder内完成双向链表的转化
TreeNode* prev = nullptr;
InOrder(pRootOfTree, prev);
// 3、通过传入的整棵树的根节点,往回找到双向链表的头结点
while(pRootOfTree->left)
{
pRootOfTree = pRootOfTree->left;
}
return pRootOfTree;
}
};
性能分析:
- 时间复杂度:O(n)。中序遍历了每一个节点。
- 空间复杂度:O(n)。每个节点都要开辟一个栈帧。
2、将有序数组转换为二叉搜索树
题目连接
解题思路:
- 首先需要了解搜索树的特点:左子树节点的值都小于根节点的值,右子树节点的值都大于根节点的值。
- 高度平衡是指左右子树高度差小于等于1。
- 又因为题目给出了有序数组,根据这个特点我们可以用中间位置的节点作为根节点,然后左区间的数组作为左子树;右区间的数组作为右子树。
完整代码:
class Solution
{
private:
TreeNode* _sortedArrayToBST(int left, int right, const vector<int>& nums)
{
if(left > right)
{
return nullptr;
}
int mid = left + (right-left)/2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = _sortedArrayToBST(left, mid-1, nums);
root->right = _sortedArrayToBST(mid+1, right, nums);
return root;
}
public:
TreeNode* sortedArrayToBST(vector<int>& nums)
{
return _sortedArrayToBST(0, nums.size()-1, nums);
}
};
性能分析:
- 时间复杂度:O(N)。
- 空间复杂度:O(N)。
3、二叉搜索树的第k大节点
题目连接
六. 其他类型题目
1、Pre-Post
题目连接
题目描述:
给出n叉树的前序和后序遍历,问该n叉树有多少种。有多组输入。
样例输入:
2 abc cba
2 abc bca
10 abc bca
13 abejkcfghid jkebfghicda
样例输出:
4
1
45
207352860
解题思路:
有人已经做过分析了,而且很详细,贴过来过来。如果一遍没看懂,建议多看几遍。
由先序和后序遍历求解符合条件的n叉树个数的方法及程序实现(福建省晋江市养正中学 张昱峥)
我们都了解二叉树的先序遍历、中序遍历和后序遍历,当知道先序遍历和中序遍历的结果时,可以唯一的确定二叉树;同样的,当知道后序遍历和中序的结果时,也可以唯一的确定二叉树。但是如果只知道先序遍历和后序遍历的结果时,二叉树就不是唯一的了,但是我们可以计算满足条件的不同二叉树的个数。同样,我们可以将问题推广到N叉树。下面我们以例题进行分析。
例一:已知二叉树的先序遍历为:abc,后序遍历为:cba,求满足条件的二叉树的个数。
分析:首先容易得出二叉树的根结点一定是a,再由剩下的先序遍历结点序列bc(第一个结点为b)和后序遍历结点序列cb(最后一个结点为b),可知结点bc共同组成根结点a的一个子树,且其中结点b一定是该子树的根结点。这个子树可以是根结点a的左子树,也可以是右子树。如下图所示:
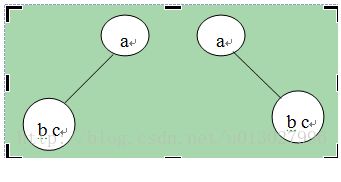
所以,满足条件的二叉树的个数sum至少为2(sum=2)。又因为对于结点bc来说,c不管是其左结点还是右结点,都满足先序和后序遍历的要求。因此满足条件的二叉树的个数sum=sum2=22=4。其形状如下图所示:
例二:已知10叉树的先序遍历为:abc,后序遍历为:bca,求满足条件的10叉树的个数。
分析:首先容易得出10叉树的根结点一定是a,再由剩下的先序遍历结点序列bc和后序遍历结点序列bc完全相同,可知结点bc不能组成根结点a的一个子树,结点b和c只能是根结点a的叶结点,并且结点b一定处于结点c的左边。因为是10叉树,所以根结点a可以有10个子结点,设编号为1~10,则结点b和c的编号可以是:(1,2)、(1,3)、(1,4)、(1,5)、(1,6)、(1,7)、(1,8)、(1,9)、(1,10)、(2,3)、(2,4)、……,由组合数知识可知符合条件的共有C2,10 = 45种。
例三:已知13叉树的先序遍历为:abejkcfghid,后序遍历为:jkebfghicda,求满足条件的13叉树的个数。
分析:首先容易得出13叉树的根结点一定是a,再由剩下的先序遍历结点序列bejkcfghid(第一个结点为b)和后序遍历结点序列jkebfghicd(最后一个结点为d),其首尾结点不一样,可知结点集合{bejkcfghid}不可能构成根结点的一个子树,也就是说,根结点a的子树至少为2个,且第1个子树的根结点必为b(由剩下的先序遍历结点序列bejkcfghid可得),再由剩下的后序遍历结点序列jkebfghicd可知,第一个子树由结点集合{jkeb}组成;而在先序遍历结点序列bejkcfghid中位于第一个子树结点集合{bejk}后的第一个结点是c,因此可推导出第二个子树的根结点必为c,再由后序遍历结点序列jkebfghicd可知其结点集合为{cfghi};同理可得第三个子树的结点集合为{d},因此,根结点a的有3个子树,因为是13叉树,所以这3个子树的形态有 C3,13种组合方式。
- 第一个子树由先序遍历结点序列bejk和后序遍历结点序列jkeb组成,设符合条件的子树数为m1;
- 第二个子树由先序遍历结点序列cfghi和后序遍历结点序列fghic组成,设符合条件的子树数为m2;
- 第三个子树由先序遍历结点序列d和后序遍历结点序列d组成,因此d为叶结点,设符合条件的子树数为1;
M1和m2的值求解同样也是由先序和后序遍历求符合条件的13叉树个数的问题,按照上述思路可递归实现,得:
![]()
因此本题满足条件的13叉树的个数为:
![]()
总结:已知n叉树的先序和后序遍历,求符合条件的n叉树的个数,解题策略为:
-
设符合条件的n叉树的个数为sum,初值为1;
-
根据n叉树的先序遍历求出根结点,根结点的子树数为k(初值为0),n叉树结点个数为m;
-
找出先序遍历中根结点后一个结点和后序遍历中根结点前一个结点,如果这两个结点相同,则n叉树只有一个子树(k=1),从树的形态上讲,这个子树可以是根结点的第1个子树或第2个子树……或第n个子树,则:
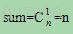
-
如果这两个结点不相同,则说明根结点存在多个子树;从后序遍历的第一个结点开始找与先序遍历中根结点后一个结点相同的结点,并记下位置t1,则后序遍历1~ t1之间的结点和先序遍历2~ t1+1之间的结点构成了根结点的第一个子树(k=1);接着从后序遍历的第t1+1个结点开始找与先序遍历中第t1+2结点相同的结点,并记下位置t2,则后序遍历t1+1~ t2之间的结点和先序遍历t1+2~ t2+1之间的结点构成了根结点的第二个子树(k=2);若t2+1
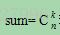
-
若根结点的k个子树只有一个结点,则结束求解,否则对根结点的k个子树按本解题策略分别进行递归求解,求解其符合条件的子树的个数sum1、sum2、sum3……、sumk;则 :
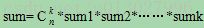
完整代码:
#include 2、二叉树的最近公共祖先
题目连接
题目描述:
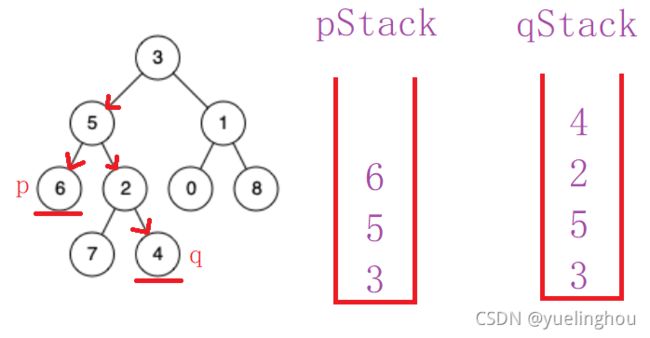
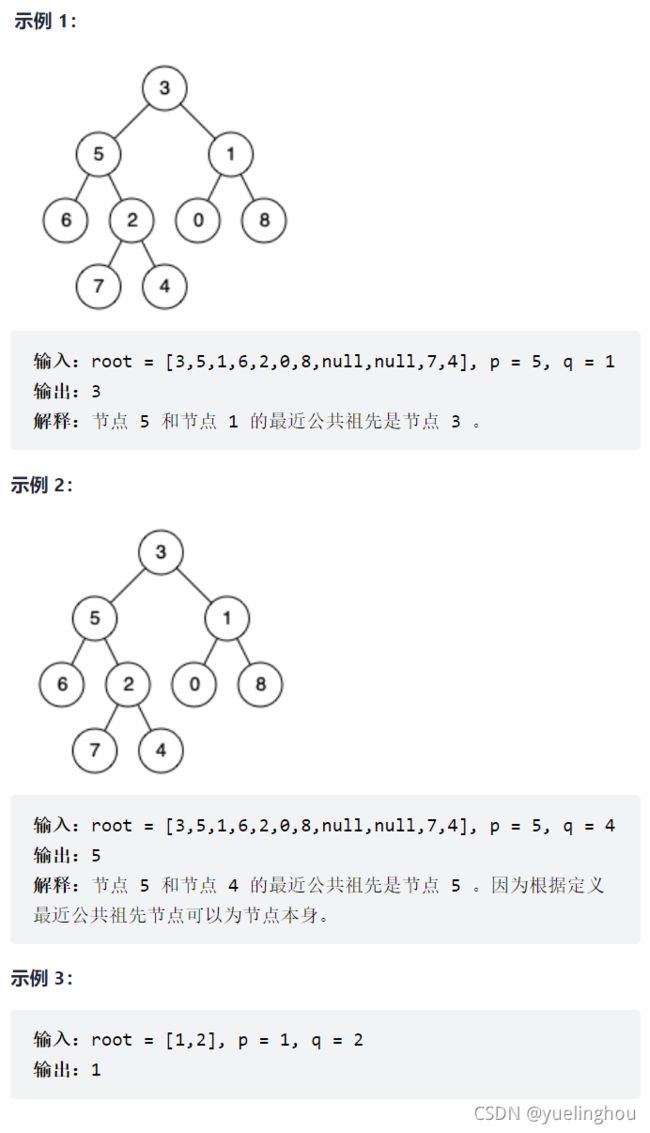
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”

解题思路:
用两个栈分别记录两个节点的路径,接下来的思路可以转化为求相交链表的第一个相交节点。
完整代码:
class Solution
{
private:
// 记录节点的路径
bool FindPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& s)
{
if(!root)
{
return false;
}
s.push(root);
if(root == x)
return true;
else if(FindPath(root->left, x, s) || FindPath(root->right, x, s))
return true;
else
s.pop();
return false;
}
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
stack<TreeNode*> pStack, qStack;
// 1、找到节点所在路径
FindPath(root, p, pStack);
FindPath(root, q, qStack);
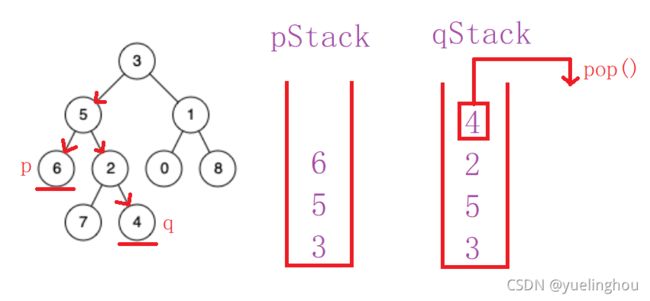
// 2、长的那个路径先走距离步
stack<TreeNode*>* longStack = &pStack;
stack<TreeNode*>* shortStack = &qStack;
if(qStack.size() > pStack.size())
{
swap(longStack, shortStack);
}
while(longStack->size() > shortStack->size())
{
longStack->pop();
}
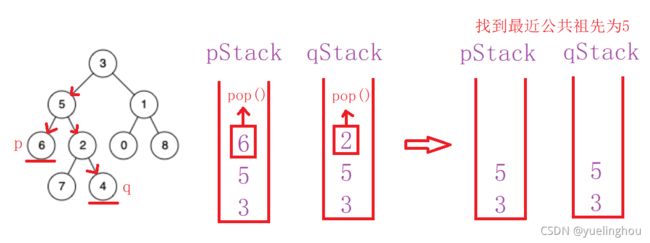
// 3、两个栈一起走,找到第一个相同的节点就是最近公共祖先
while(longStack->top() != shortStack->top())
{
longStack->pop();
shortStack->pop();
}
return longStack->top();
}
};
性能分析:
- 时间复杂度:O(n)。主要消耗在两次找找路径上。
- 空间复杂度:O(n)。查找路径时递归的栈帧消耗。