A summary on the FRI low degree test前2页导读

1. 引言

Polygon Labs Ulrich Hab¨ock 2022年论文《A summary on the FRI low degree test》，其所参考的关键论文有：

• STARK论文：Eli Ben-Sasson等人2018年论文 Scalable, transparent, and post-quantum secure computational integrity
• FRI论文：Eli Ben-Sasson等人2017年论文Fast Reed-Solomon Interactive Oracle Proofs of Proximity，即[BSBHR18a]。
• DEEP-FRI论文：Eli Ben-Sasson等人2019年论文DEEP-FRI: Sampling outside the box improves soundness，即[BSGKS20]。
• Proximity Gaps论文：Eli Ben-Sasson等人2020年论文Proximity Gaps for Reed–Solomon Codes，即[BSCI+20]。

2. A summary on the FRI low degree test论文摘要第一句

《A summary on the FRI low degree test》论文摘要中的第一句话为：

This document is an informal summary on the FRI low degree test [BSBHR18a], [BSCI+20], and DEEP algebraic linking from [BSGKS20].
即本文为对FRI、Proximity Gaps的FRI low degree test非正式总结，也为对DEEP-FRI的DEEP algebraic linking非正式总结。

相关论文有：

• 1）STARK论文提出了证明计算完整性的新方法。
  A STARK中包含了2部分：【每个都有2个版本：常规版本和DEEP版本。其中DEEP是Domain Extending for Eliminating Pretenders的简称。】
  • 1.1）an algebraic linking protocol（ALI或DEEP-ALI）：
    • 用于将计算完整性assertion，reduce为，Reed-Solomon proximity assertion。
    • 更技术的角度来说，首先将计算完整性assertion，reduce为，an “Algebraic Intermediate Representation（AIR）”，即，在algebraic linking protocol之前，需将logic checks，转换为，arithmetic checks。
  • 1.2）a Reed-Solomon proximity testing protocol（FRI或DEEP-FRI）：
    • 用于证明Reed-Solomon proximity。
• 2）FRI论文出了对“Reed-Solomon Proximity Testing problem”的新解决方案。
• 3）DEEP-FRI论文同时对ALI和FRI进行了改进。
• 4）Proximity Gaps论文展示了FRI实际优于DEEP-FRI。

当前的State-of-the-art STARK协议为：

• DEEP-ALI ＋ FRI

3. A summary on the FRI low degree test论文摘要第二句

《A summary on the FRI low degree test》论文摘要中的第二句话为：

Based on its most recent soundness analysis [BSCI+20], we discuss parameter settings for practical security levels, how FRI is turned into a polynomial commitment scheme, and the soundness of DEEP sampling in the list decoding regime.
即，基于最近的Proximity Gaps论文的soundness分析，本文讨论了：
1）实用安全级别的参数设置；
2）如何将FRI转换为多项式承诺方案；
3）在list decoding体制下，DEEP sampling的soundness。

其中包含的关键词有：

• 1）soundness分析？：
  • 即，How small is $ϵ$？（$ϵ$有多小？）
• 2）实用安全级别的参数设置？：
  • 即，如何让 $ϵ$ small？
• 3）多项式承诺方案？：
  • 即，如何在RISC Zero的interactive proof protocol中进行数据“commit”和“reveal”？
• 4）list decoding体制下的DEEP sampling soundness？：
  • 即，How secure is DEEP-ALI？

3.1 何为soundness分析？

假设你收到一个源自untrusted第三方（运行RISC Zero zkVM）的receipt，你运行该verifier并验证通过。

从中可学到什么呢？
无法保证生成receipt的不可信第三方是百分百诚实的。在ZKP以及密码学argument中，无法做到100%保证，而是获得某种概率上限$ϵ$。

• except with probability $ϵ$，该prover知道某明确满足如下约束的execution trace：
  • RISC-V ISA
  • 以及 由method_id标记的二进制文件

所谓soundness分析，其分析的就是“except with probability $ϵ$，该prover知道某明确满足如下约束的execution trace”中所关联的概率$ϵ$:

• 将$ϵ$称为soundness error。
• 通过让$ϵ$ small，可实现高级别的安全等级。

3.2 实用安全级别的参数设置？

实用安全级别的参数设置，关注的是如何让$ϵ$ small。

3.3 多项式承诺方案？

所谓承诺方案，是指：

• 一种不允许某人应答之后修改答案的方式。
• 所有的承诺方案都应具有binding属性，
• 有的承诺方案还具有hiding属性。

承诺方案中包括：

• 1）commit方法：对something进行承诺。
• 2）reveal方法：对承诺值（commitment）中的片段进行reveal。
• 3）check方法：检查所revealed片段，是否与原始承诺值匹配。

本文关注的承诺方案是基于Merkle trees的：

• 1）commit方法：通过构建Merkle tree来进行承诺，并将该Merkle tree root作为承诺值。
• 2）reveal方法：展示该Merkle tree中某叶子节点。
• 3）check方法：检查所展示Merkle叶子节点的Merkle branch。

若所承诺的数据源自evaluating a polynomial，则将相应的承诺方案称为“多项式承诺方案”。

在基于Merkle的多项式承诺方案中，该Merkle tree的每个叶子节点，对应某“evaluation domain”内的一个point。

3.4 list decoding体制下的DEEP sampling soundness？

首先，要理解“何为list decoding体制”？

Reed-Solomon Proximity Testing关注的是：

• How close is the closest Reed-Solomon codeword?
  • 有时，存在单个closest RS codeword：则在unique decoding体制。unique decoding体制下，事情都很简单。
  • 有时，存在多于一个可称为“closest”的RS codeword：则在list decoding体制。list decoding体制下，事情就更复杂刺激了。【本文关注的是list decoding体制】

4. A summary on the FRI low degree test论文摘要第三句

《A summary on the FRI low degree test》论文摘要中的第三句话为：

In particular, we illustrate the DEEP method applied to proving satisfiability of algebraic intermediate representations and prove a soundness error bound which slightly improves the one in [Sta21].
即，特别地，本文展示了用于证明algebraic intermediate representations（AIR）的DEEP方法，并证明了某soundness error bound，该soundness error bound是对StarkWare的ethSTARK论文中的小幅改进。

即，展示了使用由DEEP-ALI和FRI组成的STARK来证明某计算完整性assertion，同时，其Orbis security 要略微超过 ethSTARK security。

何为algebraic intermediate representations（AIR）？

对计算完整性的某check进行算术化，即可生成an algebraic intermediate representations（AIR）。

5. A summary on the FRI low degree test论文引言

《A summary on the FRI low degree test》论文引言中有内容：

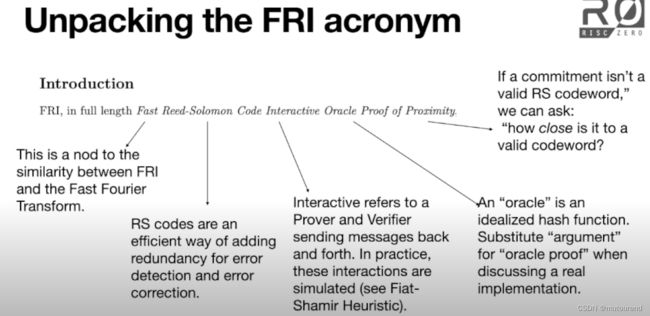
FRI，全称为Fast Reed-Solomon Code Interactive Oracle Proof of Proximity，为对函数在某FFT domain的low-degree test。所谓FFT domain，是指有限域$F$的某smooth乘法子群$D$。已知某函数$f:D\to F$，FRI证明$f$对应某low degree多项式，其degree与$D$ size相关。

即：

• Fast：类似于普遍存在的快速傅立叶变换FFT。
• Reed-Solomon Code：为错误探测和纠错添加冗余的一种高效方式。【可查看博客 Reed-Solomon Codes——RS纠错码】
• Interactive：是指Prover和Verifier相互发送消息。实际上，这些交互可模拟（具体见Fiat-Shamir Heuristic）。
• Oracle Proof："oracle"是一种理想的哈希函数。当讨论实际实现时，会将“argument”替换为“oracle proof”。
• Proximity：当某承诺值不是一个有效的RS codeword，则可问“how close is it to a valid codeword？”。

何为Code？这是Coding Theory的基础问题。


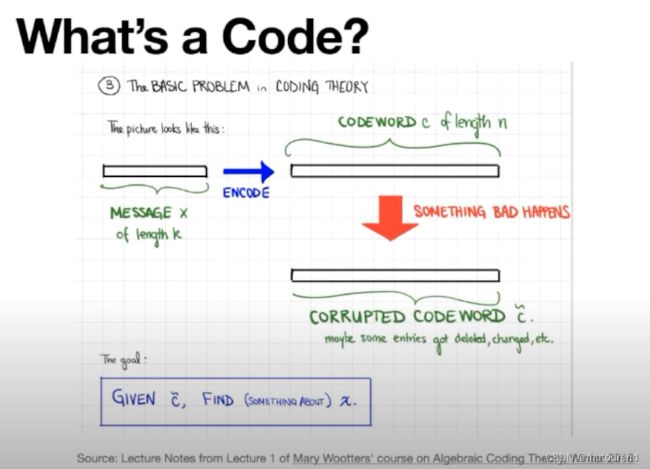
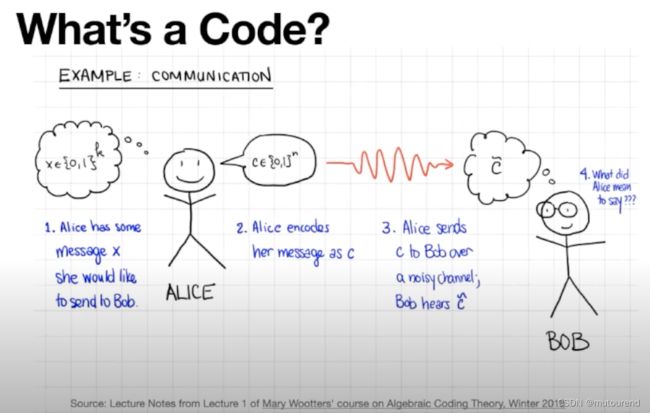
Code的正式定义为：

code理论中的distance和decoding是指：


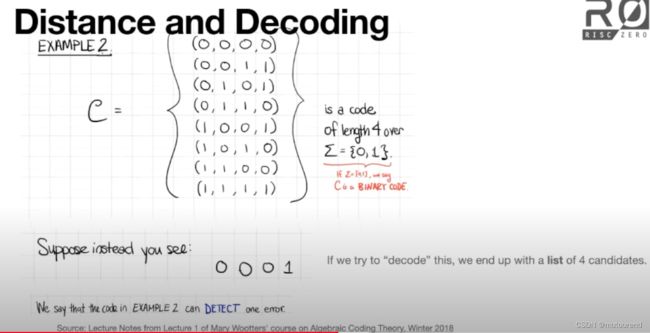
所谓distance，是指：

• 2个block之间Hamming distance，是指二者不同的元素数。

函数$f:D\to F$是指：

• 对于每个point $x\in D$，可evaluate $f(x)$。所获得的结果$f(x)\in F$。
• $D$：为“initial FRI commitment domain”，可基于$D$中的每个元素来构建一个Merkle tree叶子节点。
• $F$：为所做算术化的域。
  • 在老电路中，其为Baby Bear域。
  • 在新电路中，其为Goldilocks域。

所谓"FFT domain, i.e. a smooth multiplicative subgroup $D$ of a finite field $F$"，是指：

• FFT domain：为有利于有限域傅里叶变换的domain。
• smooth：是指可递归切分为越来越小的片段。
• a smooth multiplicative subgroup of a finite field：本文不展开讲。

《A summary on the FRI low degree test》论文引言中还提到：

由FRI Porver提供的oracles，也是基于$D$（或$D$的subdomain）的函数，FRI会仅从这些domain来选points进行query相应的values。由于$D$的size是small的（相对于polynomial IOPs的密码学large sampling space来说），区分2个多项式$f,g$的关键在于statistical sampling（统计学采样）。但是，statistical test（统计学测试）仅能保证proximity，所谓proximity，可通过做如下fractional Hamming distance来衡量：
$\delta (f,g)=\frac{1}{|D|}\cdot |x\in D:f(x)\ne g(x)|$。

所谓Testing Proximity：

• 简短来说，FRI支持test：
  • “Is the codeword I received “close enough” for me to decode?”
  • 通过几十次“queries”，可确定该codeword是否在list decoding半径范围内。
    
  • 通过更多次query，可确定该codeword是否在unique decoding半径范围内。

参考资料

[1] 2022年10月RISC Zero培训视频 Intro to FRI: RISC Zero Study Club（Slide见Study Club-FRI Summary）

RISC Zero系列博客

• RISC0：Towards a Unified Compilation Framework for Zero Knowledge
• Risc Zero ZKVM：zk-STARKs + RISC-V
• 2023年 ZK Hack以及ZK Summit 亮点记
• RISC Zero zkVM 白皮书
• Risc0：使用Continunations来证明任意EVM交易
• Zeth：首个Type 0 zkEVM
• RISC Zero项目简介
• RISC Zero zkVM性能指标
• Continuations：扩展RISC Zero zkVM支持（无限）大计算