详解LeetCode 137. Single Number II

Given an array of integers, every element appears three times except for one, which appears exactly once. Find that single one.

题意： 在一个整型数组里，只有一个数字出现一次，其他数字都出现了3次，求这个只出现一次的数字(single number)。

这真是非常非常有意思的一道题目。如果直接统计各数字出现的次数当然也能达到目的，不过空间复杂度为O(N)。能否用O(1)空间解决此问题呢？

 

首先注意到，对于某个二进制位，如果single number的该位为1，那么所有数字在该二进制位上1出现的总次数不能被3 整除，且余数为1。比如数组{3, 3, 3, 2}，转化为二进制表示： {11, 11, 11, 10}，二进制位01出现的次数为3次，二进制位10出现的次数为4次。

因此我们只需要计算出每个二进制位1出现次数除以3的余数，就可以轻松得到该single number。

模3的余数有3个： 0， 1， 2，对应二进制表示: 00, 01, 10，需要两个二进制位来表示。

我们可以用两个整数one和two来分别表示各二进制位1出现的次数模3的余数。

显然直接累加统计次数然后取模是不现实的，这时候就要用到位运算了，这也是本题解法最有技巧的一部分。

如何设计位运算模拟累加模3的结果呢？

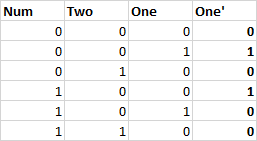
假设当前累加到数组中的数字num，考察one，two和num在二进制位取不同值下，累加1的出现次数模3的结果:

 

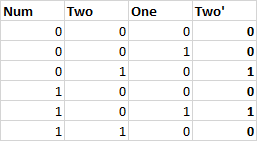
One'和Two'分别表示累加后模3的新余数的第一位和第二位。

举例

假设当前二进制位1出现的次数模3为1，数字num在该二进制位为0，那么1的出现次数不变，模3依然为1，对应两个真值表的第二行: One' = 1, Two' = 0。

假设当前二进制位1出现的次数模3为2，数字num在该二进制位为1，那么1的出现次数+1，模3结果变为0，对应两个真值表的第四行: One' = 0, Two' = 0。

因此，以上真值表就包含了所有情况下累加模3的结果。

如何将真值表转化为位运算的逻辑表达式呢？这时候就要用到一个大杀器：卡诺图 (Karnaugh map)。

以下是两个真值表转化来的卡诺图：

One'

Two'

 

解释：

列头表示num在该位为0或1的情况，行头表示当前余数的值。

两张表表内的0和1分别表示给定num和余数，进行累加模3操作后，One' 和 Two'的值，大家可以对比之前的真值表体会一下。

注意余数为11的情况是不存在的，因此结果标记为x，这列其实可以删掉。之所以写出来是为了体现卡诺图的逻辑条件是按格雷码排列的，简单说就是相邻的二进制条件只有1位是不一样的。这样方便转化为逻辑表达式的时候进行化简，简单说就是卡诺图里相邻并且构成矩形的1的情况可以简化为用一个逻辑表达式来表示。具体可以参考卡诺图Wiki页面的例子。这个问题的卡诺图比较简单，不存在化简的情况。

接下来将卡诺图转换为逻辑表达式。

以One'为例。图中只有两个格子为1，也即num = 0, two = 0, one =1 和 num = 1, two = 0, one = 0的情况。因此我们有:

one = (~num & ~two & one) + (num & ~one & ~two);

只有以上两种情况之一，one可以取值1，其他情况皆为0。注意C++里位操作符&, ^, |等的优先级低于加法操作符，因此需要括号括起来。

Two的逻辑表达式可以类推。

以下为完整代码。因为single number的1只出现一次，模3余数肯定为1，因此直接返回one即可。

int singleNumber(vector<int>& nums) {
    int one = 0, two = 0;
    for (int i = 0; i < nums.size(); i++) {
        int num = nums[i];
        int newOne = (~num & ~two & one) + (num & ~one & ~two);
        two = (~num & two & ~one) + (num & ~two & one);
        one = newOne;
    }

    return one;
}

 

转载于:https://www.cnblogs.com/k330/p/LeetCode_137_Single_Number_II.html