最小生成树算法之Prim(普里姆)算法

最小生成树的可以通过Kruskal(克鲁斯卡尔)算法或Prim(普里姆)算法求出。

Prim算法基本介绍：

Prim算法又称为"加点法"，每次找出距离(此处的距离指的是距离最小生成树的距离，若此处无法理解，可直接跳过，看完下面例子就能理解)最小的边对应的点。算法逐渐从某一个顶点s开始，逐渐将n个点纳入最小生成树中。

Prim算法基本步骤：

第一步：设图中所有顶点的集合为V，u代表已经加入最小生成树的顶点的集合，v代表未加入最小生成树的顶点的集合，最由于从某点s开始，因此u={s}，v={V-u}

第二步：在两个集合u,v中选择一条代价最小的边，将在v中连接这条边的那个顶点x加入到最小生成树顶点集合u中，并且更新与x相连的所有邻接点

第三步：重复上述步骤，直到最小生成树顶点集合u中有n个顶点为止

---

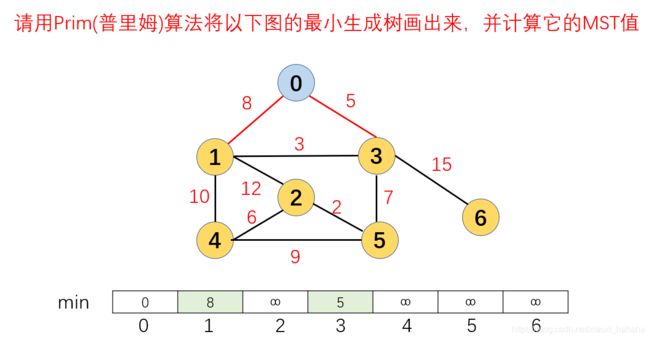
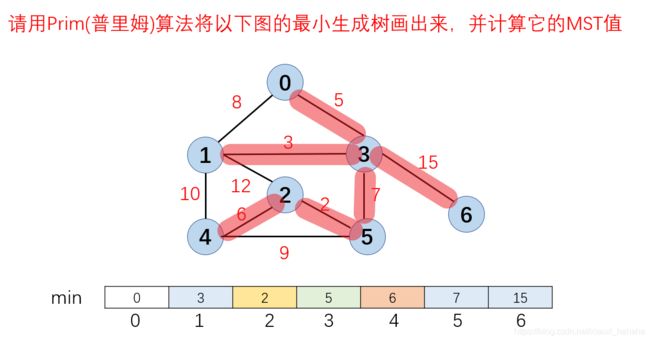
 Prim算法步骤演示，以下图为例：min数组代表，每个顶点到最小生成树的距离，以0为起点，0到最小生成树的距离就为0

  1.初始化：u={0}，v={1,2,3,4,5,6}，0加入到最小生成树集合u中，将0设置为蓝点，紧接着更新与0连接的邻接点1和3，此时0是最小生成树的一部分，1到最小生成树的距离为8，3到最小生成树的距离为5。

  2.此时u={0}，v={1,2,3,4,5,6}，在u,v两个集合中选择一条代价最小的边，下图为例就是5，根据算法步骤，将在v中连接这条边的顶点3加入到最小生成树集合u中，此时u={0,3}，v={1,2,4,5,6}。然后更新与3连接的所有顶点到最小生成树的距离，1到最小生成树的距离更新为3，5到最小生成树的距离更新为7，6到最小生成树的距离更新为15

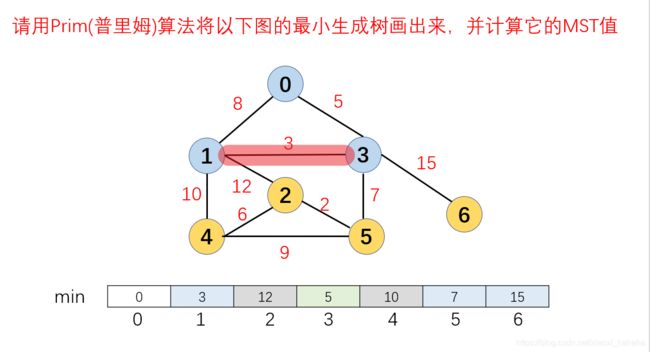
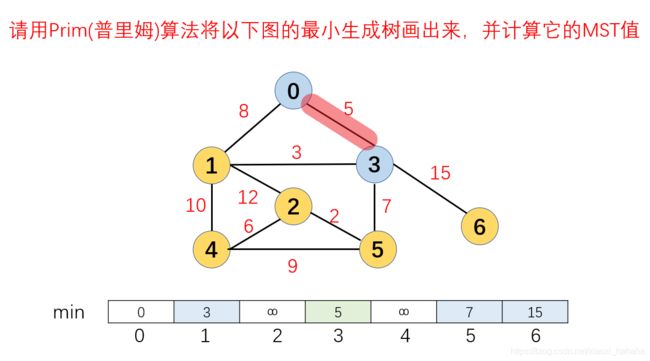  3.此时u={0,3}，v={1,2,4,5,6}，在u,v两个集合中选择一条代价最小的边，下图为例就是3，根据算法步骤，将在v中连接这条边的顶点1加入到最小生成树集合u中，此时u={0,3,1}，v={2,4,5,6}。然后更新与1连接的所有顶点到最小生成树的距离，2到最小生成树的距离更新为12，4到最小生成树的距离更新为10

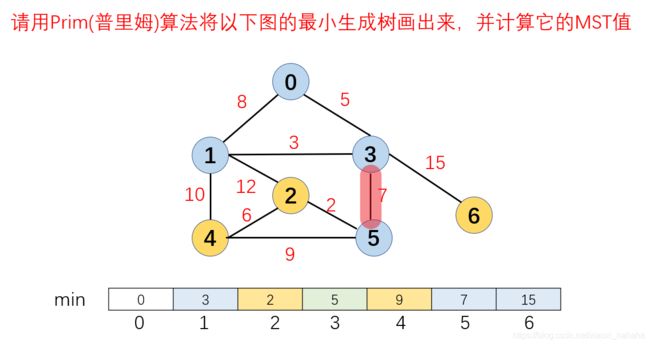
  4.此时u={0,3,1}，v={2,4,5,6}，在u,v两个集合中选择一条代价最小的边，下图为例就是7，根据算法步骤，将在v中连接这条边的顶点5加入到最小生成树集合u中，此时u={0,3,1,5}，v={2,4,6}。然后更新与5连接的所有顶点到最小生成树的距离，2到最小生成树的距离更新为2，4到最小生成树的距离更新为9

  5.此时u={0,3,1,5}，v={2,4,6}，在u,v两个集合中选择一条代价最小的边，下图为例就是2，根据算法步骤，将在v中连接这条边的顶点2加入到最小生成树集合u中，此时u={0,3,1,5,2}，v={4,6}。然后更新与2连接的所有顶点到最小生成树的距离，4到最小生成树的距离更新为6

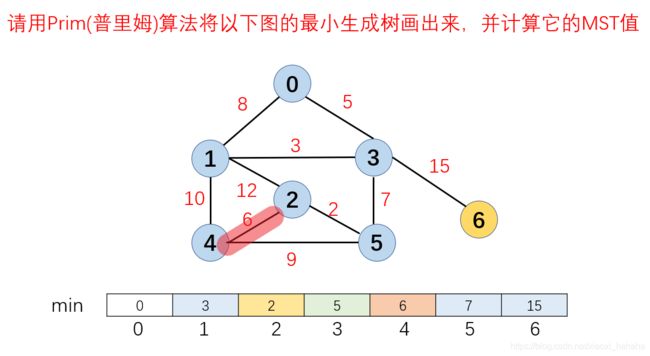
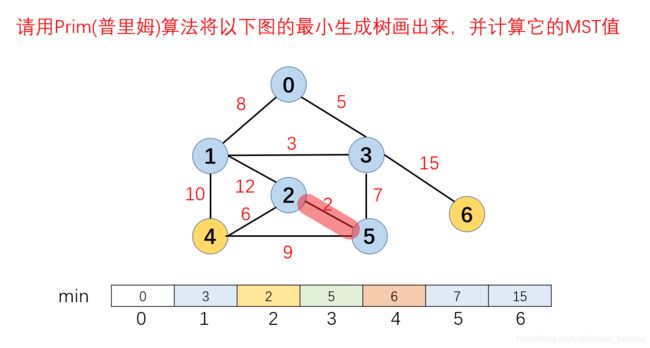  6.此时u={0,3,1,5,2}，v={4,6}，在u,v两个集合中选择一条代价最小的边，下图为例就是6，根据算法步骤，将在v中连接这条边的顶点4加入到最小生成树集合u中，此时u={0,3,1,5,2,4}，v={6}。然后更新与4连接的所有顶点到最小生成树的距离，发现4没有邻接点可以更新

  6.此时u={0,3,1,5,2,4}，v={6}，在u,v两个集合中选择一条代价最小的边，下图为例就是15，根据算法步骤，将在v中连接这条边的顶点6加入到最小生成树集合u中，此时u={0,3,1,5,2,4,6}，v={}。然后更新与6连接的所有顶点到最小生成树的距离，发现6没有邻接点可以更新

 

Prim算法执行完成后得到的最小生成树为：

最终，将min中的值进行求和，结果为0+3+2+5+6+7+15=38，因此MST的值为38。有兴趣的朋友可以以此题为例，利用Kruskal算法求出最小生成树。

你若盛开,蝴蝶自来;你若精彩,天自安排！算法学习贵在坚持，各位小伙伴们要坚持噢！如果对于以上博文有任何疑问，可以联系本人。wechat：Q1313135