关于深度学习高维矩阵的形象化理解
对于初次接触深度学习的小白来说,高维张量总是很难理解,在我理解高维张量的本质后,也理解了之前阻拦我理解的问题点,所以写下这篇博客,用常用的三个对张量操作的函数进行解释,希望对后面学习的人有所帮助。
目录
重新理解permute
重新理解flatten
重新理解sum
首先先给出最重要的两点,后面会做出解释:
- 搞清楚该张量的最小组成单元是什么
- 不要尝试用几何解释高维张量
对于任何一个高维张量,它们都会只有一个最小单元。而这个张量的每一个维度就是对该单元的分类,例如在简单的分类中最后输出的二维矩阵(num_inputs, num_class)。num_inputs是每次输入的x个数,num_class是分出的种类。如果是猫狗识别,我们一次输入5张图片,而种类有猫狗两种,num_inputs就为5,num_class就为2,这里的最小单元就是概率。当然,没接触过分类的朋友可能不是很明白,后面我会用更加具体的例子。
有一个场景需要我们来预测苹果的价格,这个价格由三个要素决定,即种类,产地,品质
如果以上面三个要素产生一个shape为(3,2,2)的张量X,这个张量的最小单位是价格,那么X[0][0][0]就是 好的 南部 黑苹果 的价格。
这看起来似乎很容易理解,那么我现在给X带上具体数值:
x = torch.arange(12,dtype=torch.float32)
x = x.reshape(3,2,2)
print(x)
重新理解permute
如果我现在使用 x = torch.permute(x,(1,0,2)) 来调换x的0和1维度,你能准确说出转换后每个位置的数值吗?我想有些人一下就懵了,其中有些人就没做到第二点:不要尝试用几何解释三维。几何做法就是用一个3*2*2的矩阵旋转一下,我们先不说这个方法没法解决三维以上的问题,就算真的这样做也很难迅速报出答案。
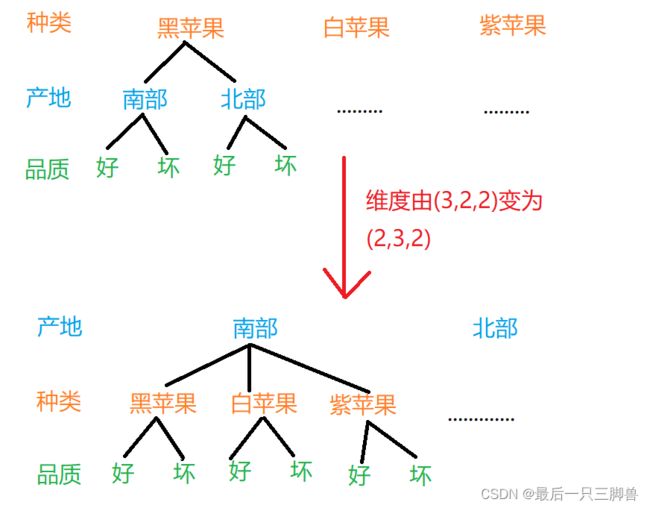
想要快速知道结果,只要搞清维度调换的本质就可以了。维度的变化可以用下图来表示:
原来的(0,0,0)是黑南好,现在是南好黑,所以维度转化后是不变的, 但原来的(1,0,0)是白南好,现在是北黑好,所以只要找到之前北黑好的价格就知道该点变化后的数值了。
转化后的张量:
可以看出,维度的变化只是在分类的顺序上变化了,如果维度是(a,b,c),就是先将数据在a上分类,然后是b和c,转换了维度,就是转换了分类顺序。知道这一点对后面的理解至关重要!
重新理解flatten
flatten(tensor, start_dim=0)是将一个张量从start_dim维度展平为1维向量,默认是从0维展平。
x = torch.arange(12,dtype=torch.float32)
x = x.reshape(3,2,2)
x = torch.permute(x,(1,0,2)) #转换维度(3,2,2)->(2,3,2)
print(x)
x = torch.flatten(x)
print(x)你能看出最后输出的一维向量的意义吗?其实我只要把每个数字对应的含义标出来你就能立马明白。0,1,4,5,8,9都是南部的苹果;0,1是黑苹果,4,5是白苹果,8,9是紫苹果;0是好苹果,1是坏苹果...这样你应该就能看出flatten的作用了吧。其实就是在一维向量里把苹果依次分类,即按照产地、种类、品质进行分类,产地就为”最外类“。
重新理解sum
x = torch.arange(12,dtype=torch.float32)
x = x.reshape(3,2,2)
print(x)
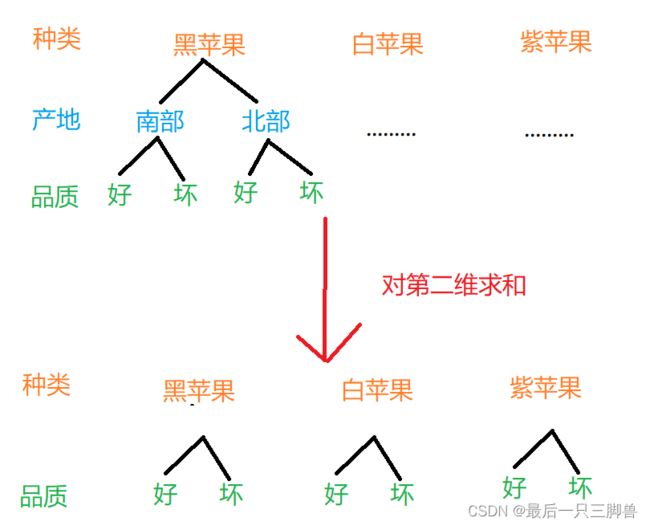
print(x.sum(1))这里的结果直接去想很难想出来,必须要结合意义去理解。这里把第二维求和,也就是把产地维度进行求和了,可用下图表示:
原来有黑南好、黑南坏、黑北好、黑北坏,现在只有黑好和黑坏了,即黑好 = 黑南好 + 黑北好,黑南好为(0,0,0)的0,黑北好为(0,1,0)的2,0+2=2就是求和后的黑好(0,0)的结果。这样你是否能更加直观的理解了呢?
切记:这里代入数值只是为了验证这样的理解没有问题,在实际学习中我们需要做的是理解这样做的意义,不要代入数值去思考!
有问题请评论提出,感谢支持!!!