LeetCode热题 100整理
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的 升序 排列数组
-104 <= target <= 104
思考:
找到第一个大于等于target的位置即可。
class Solution {
public:
int searchInsert(vector& nums, int target) {
int len = nums.size();
int res;
for (int i = 0; i < len; i++) {
if (nums[i] >= target) {
res=i;
break;
}
}
return res;
}
}; 53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
题目分析:
思考1:从第一个数开始累加,找到累加最大的数和最小的数,然后用最大的减去最小的。其中最大的数要在最小的数右边。结果失败,忽略了一个数字的时候以及整个数列都是负数时,会运行错误。
代码如下:
class Solution {
public:
int maxSubArray(vector& nums) {
int len = nums.size();
int sum = 0;
int a[100002];
a[0] = 0;
int max = a[0];
int min = a[0];
if (len <= 1) {
return nums[0];
}
else
{
for (int i = 0; i < len; i++) {
sum += nums[i];
a[i + 1] = sum;
}
int maxi;
for (int i = 0; i < len + 1; i++) {
if (a[i] >= max) {
max = a[i];
maxi = i;
}
}
for (int j = 0; j < maxi; j++) {
if (a[j] <= min) {
min = a[j];
}
}
int res = max - min;
return res;
}
}
}; 思考2:通过动态规划的思想,依旧是从前往后加,但是如果前一个是负数,就不要累加,重新加当前的值。最后找最大的累加值即可。
代码如下:
class Solution {
public:
int maxSubArray(vector& nums) {
int n = nums.size();
int maxnum = nums[0];
for (int i = 1; i < n; i++) {
if (nums[i - 1] > 0) {
nums[i] += nums[i - 1];
}
maxnum = max(maxnum, nums[i]);
}
return maxnum;
}
}; 73. 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用原地算法。
示例 1:
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
思考:
原地算法即为改原本的数组,但是改了原本的数组在后面判断时就不知道是原本的0还是修改后新的0,因此需要再复制一个数组,然后在新的数组里进行查找0,然后修改原本的数组。
代码如下:
class Solution {
public:
void setZeroes(vector>& matrix) {
vector> cop(matrix);
int m = matrix.size();
int n = matrix[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (cop[i][j] == 0) {
for (int k = 0; k < n; k++) {
matrix[i][k] = 0;
}
for (int h = 0; h < m; h++) {
matrix[h][j] = 0;
}
}
}
}
}
}; 118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30
代码如下:
class Solution {
public:
vector> generate(int numRows) {
vector> a(numRows);
// a[0][0]=1;
// a[1][0]=1;
// a[1][1]=1;
for (int i = 0; i < numRows; i++) {
a[i].resize(i + 1);
for (int j = 0; j <= i; j++) {
if (i == 0 || i == 1 || j == 0 || j == i) {
a[i][j] = 1;
}else{
a[i][j] = a[i - 1][j] + a[i - 1][j - 1];
}
}
}
return a;
}
}; 160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
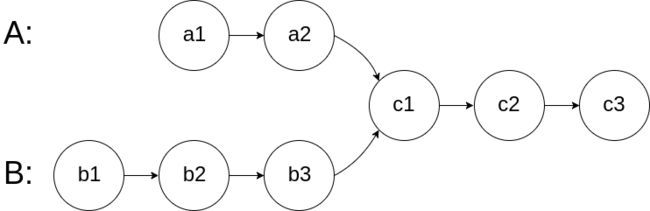
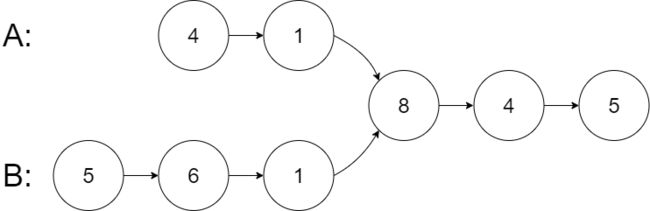
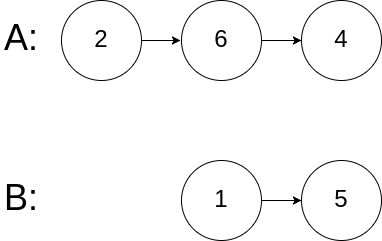
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA中节点数目为mlistB中节点数目为n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n- 如果
listA和listB没有交点,intersectVal为0 - 如果
listA和listB有交点,intersectVal == listA[skipA] == listB[skipB]
思考:
找到第一个数字相同的数字即可,可以先将其中一个链表存入set集合中,然后与另一个链表作比较,找到相同数字的位置。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
unordered_set visited;
ListNode *temp = headA;
while(temp!=nullptr){
visited.insert(temp);
temp = temp->next;
}
temp = headB;
while(temp!=nullptr){
if(visited.count(temp)){
return temp;
}
temp = temp->next;
}
return nullptr;
}
}; 206.反转链表
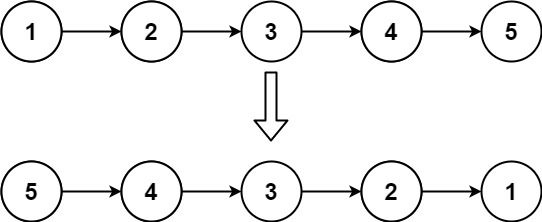
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2] 输出:[2,1]
示例 3:
输入:head = [] 输出:[]
提示:
- 链表中节点的数目范围是
[0, 5000] -5000 <= Node.val <= 5000
思考:
通过画图完成,但我不懂的一点为什么还要定义一个next指针,直接用后面的为什么输出的只有一个数字。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
ListNode* curr = head;
while(curr){
ListNode* next = curr->next;
curr->next=prev;
prev = curr;
curr = next;
}
return prev;
}
};
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
进阶:
你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组不被视为额外空间。)
思考:
题目提示了全部前缀元素和后缀的乘积,因此可以想到求该元素的前缀之积乘上后缀之积,为了不占空间,可以直接通过answer来赋值前缀积,然后后缀积新定义一个字母用来计算即可。
代码如下:
class Solution {
public:
vector productExceptSelf(vector& nums) {
int len = nums.size();
int l=1;
vector answer(nums.size());
answer[0] = 1;
for (int i = 1; i < len; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
for (int i = len-1; i >=0; i--) {
answer[i] *= l;
l *= nums[i];
}
return answer;
}
};