NEFU离散数学实验特别篇1-树和图
树相关概念
离散数学中,树是一种重要的数据结构,它是一种无向连通图,并且不存在环。下面是树的相关概念和公式:
1. 顶点数为n的树,边数为n-1。
2. 度数为k的树中有k个分支。
3. 一棵树中最多只有两个度数大于1的顶点,这些顶点称为树的端点或叶子,其余顶点称为分支或内部点。
4. 一棵有n个顶点的满二叉树,深度为h,共有2^(h+1)-1个结点,其中叶子结点数为2^h。
5. 一棵有n个顶点的完全二叉树,深度为h,共有2^h个结点,其中叶子结点数为2^(h-1)或2^h。
6. 一棵二叉树的深度为h,最多有2^h-1个结点,最少有h个结点。
7. 一棵n个结点的树,最多h=n-1,最小为1,树的高度即为树的深度。
8. 一个树森林(由若干棵树组成)中,所有树的节点数n等于边数m+森林中树的棵树。
9. 一棵树的生成森林中,边数为n-1。
10. 一颗有n个顶点的有根树,每个顶点都有度数,度数为0的顶点称为叶子顶点,度数不为0的顶点称为内部顶点,如果叶子顶点的数量为m,那么内部顶点的数量为n-m。
1. (程序题)2元完全正则树
思路
P178概念题目啦
知道啥是2元完全正则树即可
概念拆分:
r元树:T的每个分支点至多有r个儿子
r元正则树:T的每个分支点恰好有r个儿子
r元完全正则树:T是r元正则树,且所有树叶的层数均为树高
树的层数:树根到任意一点的通路长度
树的高:最大层数
可以发现,对于树高为h的2元完全正则树
顶点数=
边数=0+2+4+8+16....
树叶=
#include
#include
#include
int main(){
int h;
scanf("%d",&h);
int edge=0;
for(int i=1;i<=h;i++)edge+=1<<(i);
printf("%d %d %d",(1<<(h+1))-1,edge,1< 2. (程序题)树的边数
思路
2元正则树:T的每个分支点恰有2个儿子
其实想想最特殊的情况,2元完全正则树嘛(可以先看后面的一道题目)
可以发现m = 2 ( t − 1 ) m=2(t-1)m=2(t−1)
#include
#include
#include
int main(){
int t;
while(~scanf("%d",&t)){
printf("%d\n",2*(t-1));
}
return 0;
}
图相关概念
离散数学是一门研究离散化的数学学科,图论是其中的一个分支,涉及到一些基本概念和公式,包括:
1. 图的基本概念:
- 顶点(vertex):图中的节点。
- 边(edge):连接顶点的线段。
- 无向图(undirected graph):图中的边没有方向。
- 有向图(directed graph):图中的边有方向。
- 加权图(weighted graph):图中的边带有权值。2. 图的表示方法:
- 邻接矩阵:用一个矩阵来表示图中顶点之间的关系。
- 邻接表:用链表来存储图中顶点之间的关系。
- 关联矩阵:用一个矩阵来表示图中边与顶点之间的关系。
1. (程序题)度数序列
思路
可以看一下书本P135的例6.3
根据握手定理:所有顶点度数之和为边数两倍。
那么有推论,奇度顶点的个数一定是偶数的。
#include
#include
#include
int main(){
int n;
while(~scanf("%d",&n)){
int cnt=0;
for(int i=1,x;i<=n;i++){
scanf("%d",&x);
if(x&1)cnt++;// 如果x是奇数,计数器cnt加1
}
if(cnt&1)puts("no"); // 如果计数器cnt是奇数,输出"no"
else puts("yes");
}
return 0;
} 2. (程序题)平面图
思路
书本P159定理6.16
设G为任意的连通的平面图,则n-m+r=2。其中n为顶点数,m为边数,r为面数满足n-m+r=2
#include
#include
#include
int main(){
int n,r;
while(~scanf("%d%d",&n,&r)){
printf("%d\n",n+r-2);
}
return 0;
}
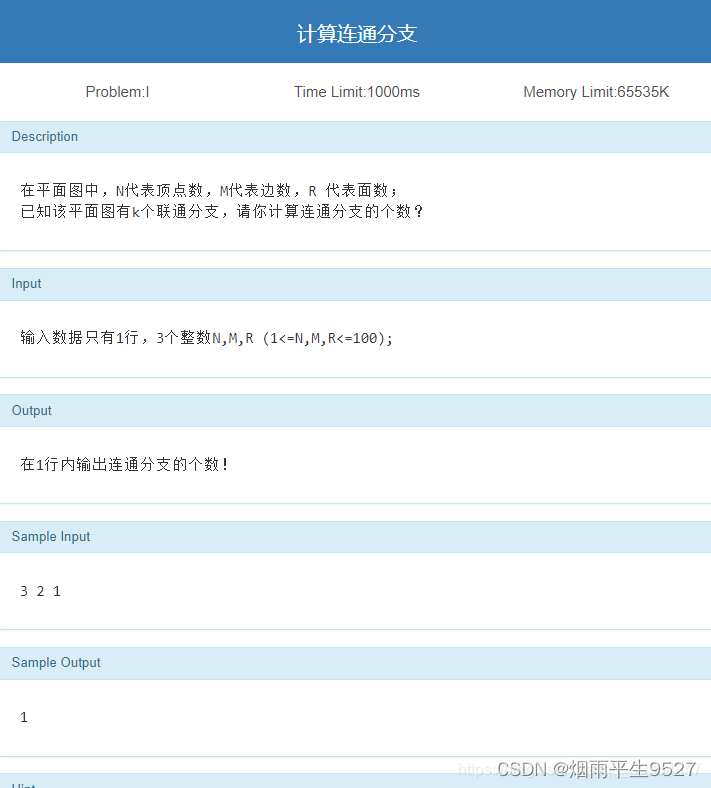
3. (程序题)计算连通分支数
思路
书P159推论
G是具有k(k>=2)个连通分支的平面图,则n-m +r=k +1
#include
#include
#include
int main(){
int n,m,r;
scanf("%d%d%d",&n,&m,&r);
printf("%d",n-m+r-1);
return 0;
} 4. (程序题) 求悬挂顶点
思路
根据握手定理:所有顶点度数之和为边数两倍
悬挂顶点度数为1。
设有x个悬挂顶点2m=(2+3+4+5+6)t+x
x=2m-20t
#include
#include
#include
int main(){
int m,t;
scanf("%d%d",&m,&t);
printf("%d",2*m-20*t);
}