图像传感器与信号处理——自动曝光算法

图像传感器与信号处理——自动曝光算法

我是搞视觉SLAM的，在很久之前我和一位视觉SLAM大佬交流过，视觉SLAM难以落地原因有很多，其中之一就是环境光照对SLAM系统有较大的影响，而在实际的应用过程中，我们很难去真正控制环境中的光照变化，尤其是在室外。因此如何使得输入SLAM系统的图像具备稳定的光照就是非常值得研究的，而自动曝光就是其中一个非常重要的解决方案。这就是我这几天在家看这几篇论文的出发点。

1. 如何实现自动曝光？

自动曝光的过程是一个经典的反馈控制过程。

首先，既然是控制我们就需要知道控制的是什么，对于一般的相机来说，和曝光相关的参数配置有光圈、曝光时间、增益等，其中光圈的配置必须通过硬件实现，因此在实际操作过程中一般只控制曝光时间和增益来实现自动曝光。

其次，既然是反馈我们就需要建立一个标准来衡量曝光程度的优劣，而这个衡量标准定义的不同则意味着自动曝光算法的不同，下文就是据此对自动曝光算法进行分类，分别是基于直方图统计的算法、基于图像熵的算法、基于梯度的算法。

2. 基于直方图统计的算法

基于直方图统计的算法相关文章较多，而且都比较旧想法也比较简单，下面这些文章都是基于直方图统计的算法：
（1）An Advanced Video Camera System with Robust AF, AE, and AWB Control，2001
（2）Real-time Image Fusion and Adaptive Exposure Control for Smart Surveillance Systems，2007
（3） 2.3 Automatic Camera Exposure Control，2007
（4） 2.4 Autonomous Configuration of Parameters in Robotic Digital Cameras，2009
这里只对下面这篇比较新的一篇论文进行分析：

2.1 Acquisition of Agronomic Images with Sufficient Quality by Automatic Exposure Time Control and Histogram Matching，2013

这篇文章主要描述的是一个在农用机器人上应用的实际场景，最终目的是通过自动曝光实现农用机器人更加准确地识别稻田里面的特征。对于自动曝光算法，其在图像直方图的基础上有了进一步的改进，算法框架如下图所示：

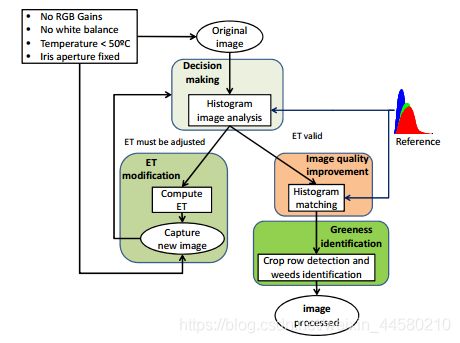
除了通过图像直方图计算曝光时间外，还会通过直方图匹配对曝光后的图像进行进一步优化。这篇文章采用的归一化直方图，首先计算：$${\mu }_n(g)=\sum _{\epsilon }(g-m{)}^{n}p(g)\text{ with }m=\sum _{s}g\cdot p(g)$$其中$g$的即直方图的横坐标，其范围是$0$到$255$，$p(g)$是横坐标$g$在直方图中对应的值，$m$是平均值在此基础上可以计算方差$v={\mu }_2(g)$、偏度$\gamma ={\mu }_3(g){\mu }_2^{-3/2}(g)$和峰度$\kappa ={\mu }_4(g){\mu }_2^{-2}(g)$，这篇文章中用于Decision making的两个参数是平均值$m$和偏度$\gamma$，如下所示：

$$\text{ while }\left(m_i\ge m_{ui}\text{ and }{\gamma }_i\ge \left|{\gamma }_{ui}\right|\right)\text{or}\left(m_i\le m_{li}\text{ and }{\gamma }_i\ge {\gamma }_{li}\right)$$$$ET=\left(\frac{m_{Rref}+m_{Gref}}{m_R+m_G}\right)E{T}_{curr}$$其中$m_i$和${\gamma }_i$为图像第$i$个通道的均值和偏度（红绿蓝三个通道，但是由于农用场景的限制，这篇文章只考虑红和绿两个通道），$m_{ui}$和$m_{li}$分别是均值的最大最小边界，${\gamma }_{ui}$和${\gamma }_{li}$分别是偏度的最大最小边界。$m_{Rref}$和$m_{Gref}$分别为参考图像的直方图平均值，通过上式就可以计算出优化后的曝光时间，即ET modification中的过程。
如果在Decision making中判定不需要进行曝光时间优化后就可以直接进行Image quality Improvement，其流程是分别计算输入图像和参考图像的直方图的累加概率$$P\left(g_r\right)=\sum _{i=0}^{{\epsilon }_s}p\left(g_i\right)\text{ and }P\left(g_c\right)=\sum _{i=0}^{R}p\left(g_c\right)$$通过累加概率进行匹配，然后搜索最接近的$P\left(g_r\right)$值，然后用$g_r$改变$g_c$（这里论文中是这么说的，但是具体如何改变并没有举例说明，具体怎么实现的会有点不清楚）。

3. 基于熵的算法

基于熵的自动曝光算法相关的文章好像并不多，目前就找到这一篇比较有代表性的：

3.1 Camera Parameters Auto-Adjusting Technique for Robust Robot Vision，2010

这篇文章主要是介绍了一种基于图像熵的摄像机参数自动调节技术，根据香农定理信息内容可以通过熵进行描述，并且熵可以随着信息内容增加而增大。在RGB色域中计算图像熵，公式如下：$$\begin{array}{rl}\text{Entropy}=& -\sum _{i=0}^{L-1}{P}_{Ri}\log P_{Ri}-\sum _{i=0}^{L-1}{P}_{Gi}\log P_{Gi}-\sum _{i=0}^{L-1}{P}_{Bi}\log P_{Bi}\end{array}$$其中，$L=256$为RGB颜色通道的离散范围，$P_{Ri},P_{Gi},P_{Bi}$分别是颜色$Ri,Gi,Bi$在图像中的概率，由上式可知$$0=\mathrm{Min}(\text{ Entropy })\le \text{ Entropy }\le \mathrm{Max}(\text{ Entropy })=-3\ast \sum _{i=0}^{255}(1/256)\log (1/256)=16.6355$$文章中提到控制的参数为曝光时间和增益，那么通过实验可以测得图像熵随曝光时间和增益这两个参数变化的趋势如下图所示：
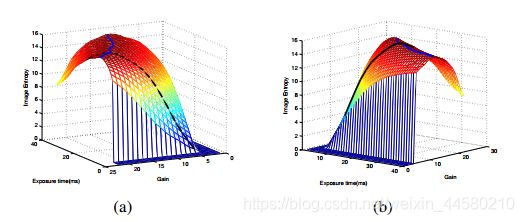其中图中蓝色背脊线上的参数都是可以接受的，但是如上图所示的这种三维图是不方便搜索最佳参数的，因此在实际应用中，将曝光时间和增益设置为相同的数值，这样就可以将三维图转化为如下图所示的二维图：

其中图（a）是室内测得的图像熵随参数变化的曲线，图（b）是室外测得的图像熵随参数变化的曲线，如图所示，图像熵随着参数呈单调递增再单调递减的变化趋势。因此搜索就变得简单，可以从一个较低的曝光时间和增益开始，以一定的步长朝峰值搜索，直到下一步的图像熵小于当前步，那么就寻找到了最优的曝光和增益。

4. 基于梯度的算法

这是最近几年比较热门的一种算法，起码对于SLAM来说，实验证明这些算法是有效的，这里分享两篇方法比较类似的文章：

4.1 Active Exposure Control for Robust Visual Odometry in HDR Environments，2017

题目直抒胸臆呀，就是通过自动曝光控制提高视觉里程计在高动态环境下的鲁棒性。这篇文章中提出了在视觉里程计中应用自动曝光需要解决的问题是，一方面需要最大化图像信息，另一方面需要补偿由于曝光时间调整带来的时间差。

首先解决第一个问题，如何最大化图像信息，首先论文中定义了光度响应函数$$I=f(X)=f(E\Delta t)$$其中，$I$为图像的光照强度，辐照度$E$描述了单位时间射入像素的能量，$\Delta t$为曝光时间，而这个函数本身$f$是很难有具体的表达式的，这也就是为什么在自动曝光系统中采用的多是反馈控制算法，如果有了光度响应函数的具体表达式，我们就可以通过这个表达式直接获得合适的曝光时间。在此基础上定义了逆响应函数$$g=\ln f^{-1}$$这个逆响应函数并不是直接对响应函数求逆，那么光度响应函数的逆响应函数如下：$$\tilde{g}(I)=\ln E+\ln \Delta t$$我们通过采集不同的曝光时间$\Delta t$的图像，并计算图像的光照强度$I$，这样就可以看做获得了一组离散数据$g(k),k=0,1,\dots ,Z_{\max }$，然后利用这组数据采用十阶的多项式函数进行拟合函数 $g$，获得函数 $g$后可以进一步函数的微分形式$g^{\prime }$，如下图所示就是这样一条曲线：

有了这个基础后，下面进一步建立曝光程度的评价标准，论文中建立了四种标准，并对标准进行了讨论对比，首先将像素$\mathbf{u}$的梯度幅值定义为：$$G(\mathbf{I},\mathbf{u},\Delta t)=\Vert \nabla \mathbf{I}(\mathbf{u},\Delta t){\Vert }^2$$其中$\nabla \mathrm{I}(\cdot )=\left[\frac{\partial \mathrm{I}}{\partial x},\frac{\partial \mathrm{I}}{\partial y}\right]$，那么四种标准分别是：
（1）直接求和：$$M_{\mathrm{s}\mathrm{u}\mathrm{m}}=\sum _{{\mathbf{u}}_i\in \mathrm{I}}G\left({\mathbf{u}}_i\right)$$
（2）对数求和：$$M_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{m}}=\sum _{{\mathbf{u}}_i\in \mathrm{I}}{m}_{{\mathbf{u}}_i}$$其中$$m_{{\mathbf{u}}_i}=\{\begin{array}{ll}\frac{1}{N}\log \left(\lambda \left(\tilde{G}\left({\mathbf{u}}_i\right)-\sigma \right)+1\right),& G\left({\mathbf{u}}_i\right)\ge \sigma \\ 0,& G\left({\mathbf{u}}_i\right)<\sigma \end{array}$$这种评价标准在下一篇论文中作更加详细的分析。

（3）百分位数$$M_{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}}(p)=\text{ percentile }\left({\left\{G\left({\mathbf{u}}_i\right)\right\}}_{{\mathbf{u}}_i\in \mathrm{I}},p\right)$$其中，$\text{ percentile }$函数是求百分位数，例如当参数 $p$ 为0.5时，那么$M_{\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}}(p)$就是所有梯度幅值中的中位数。

（4）软百分位数$$M_{\text{softperc }}(p)=\sum _{i\in [0,S]}{W}_{i\mathrm{h}}(p)\cdot G_{i\mathrm{t}\mathrm{h}}$$其中$S$为图像中所有像素的数量，$G_{i\mathrm{t}\mathrm{h}}$为排好序的梯度幅值，而权重$W_{i\mathrm{h}}$定义如下：$$W_{i\mathrm{h}}=\{\begin{array}{ll}\frac{1}{N}\sin {\left(\frac{\pi }{2[p\cdot S]}i\right)}^k,& i\le \lfloor p\cdot S\rfloor \\ \frac{1}{N}\sin {\left(\frac{\pi }{2}-\frac{\pi }{2}\frac{i-\lfloor p\cdot S\rfloor }{S-\lfloor p\cdot S\rfloor }\right)}^k,& i>\lfloor p\cdot S\rfloor \end{array}$$其中符号$\lfloor \cdot \rfloor$为向下取整。

在论文中，通过对比FAST角点在各自标准下最优图像提取数量进行实验对比，发现百分位数标准和软百分位数标准提取数量会更多，然后还通过下面这张图进行图进行直观效果说明，我觉得很有意思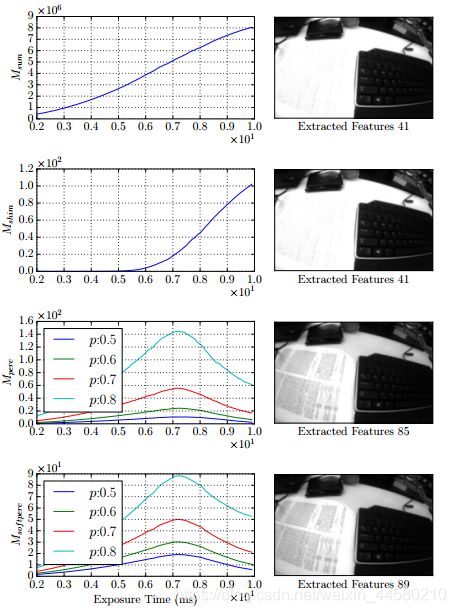：从上到下分别是四个评价标准计算的值随曝光时间的变化曲线，可以看到，前两者是随着曝光时间单调上升，而在最顶点是已经出现了过曝光的情况，后两者则不会，曲线有极大值，而在极大值时图像曝光对于细节的保留确实较优。

最后说明如何根据评价标准和光度响应函数进行自动曝光控制了，那么要做的就是将评价标准$M$对曝光时间$\Delta t$求导，然后通过梯度下降法求得极大值，那么不管采用上面哪种评价标准，中间都包括求$\frac{\partial G(\cdot )}{\partial \Delta t}$，那么有$$\frac{\partial G(\cdot )}{\partial \Delta t}=2\nabla \mathbf{I}(\mathbf{u},\Delta t{)}^{\top }\frac{\partial }{\partial \Delta t}[\nabla \mathbf{I}(\mathbf{u},\Delta t)]$$根据二阶导数的对称性，有$$\frac{\partial }{\partial \Delta t}[\nabla \mathbf{I}(\mathbf{u},\Delta t)]=\nabla \left[\frac{\partial }{\partial \Delta t}\mathbf{I}(\mathbf{u},\Delta t)\right]$$求$\frac{\partial \mathbf{I}}{\partial \Delta t}$就需要用到我们前面提到的光度响应函数$$\frac{\partial \mathbf{I}}{\partial \Delta t}=\frac{f(E(\mathbf{u})\Delta t)}{\partial \Delta t}=f^{\prime }\left(E(\mathbf{u})\Delta t\right)E(\mathbf{u})=f^{\prime }\left[f^{-1}(\mathbf{I})\right]E(\mathbf{u})=\frac{E(\mathbf{u})}{{\left[f^{-1}\right]}^{\prime }(\mathbf{I})}=\frac{1}{g^{\prime }(\mathbf{I})\Delta t}$$其中，最后一个等式是因为前面定义的逆响应函数$$g(\mathbf{I})=\ln f^{-1}(\mathbf{I})$$那么对$g$求导有$$g^{\prime }(\mathbf{I})=\frac{{\left[f^{-1}\right]}^{\prime }(\mathbf{I})}{f^{-1}(\mathbf{I})}=\frac{{\left[f^{-1}\right]}^{\prime }(\mathbf{I})}{E(\mathbf{u})\Delta t}$$将上式变形代入即可。因为$g^{\prime }(\mathbf{I})$在一开始就介绍了如何通过采样拟合求得，那么最终$\frac{\partial G(\cdot )}{\partial \Delta t}$就可求得，就可以通过梯度下降法求得极大值。以$M_{\text{softperc }}(p)$为例，我们可以求得其关于曝光时间$\Delta t$的导数有：$$\frac{\partial M_{\text{softperc }}}{\partial \Delta t}=\sum _{i\in [0,S]}{W}_{i\text{ th }}\frac{\partial G_{ith}}{\partial \Delta t}$$那么曝光时间的更新方式为：$$\Delta t_{\text{next }}=\Delta t+\gamma \frac{\partial M_{\text{softpere }}}{\partial \Delta t}$$关于自动曝光的部分这篇文章就介绍到这里，文章后面一部分是进行曝光补偿，这个稍后介绍

4.2 Gradient-based Camera Exposure Control for Outdoor Mobile Platforms，2018

这篇文章中提出要解决的问题一方面是如何进行基于图像梯度的自动曝光控制，另一方面是如果实现多相机联合曝光。

首先解决第一个问题，这篇文章提出，自然场景图像的梯度分布满足重尾分布，也就是场景中大部分梯度的幅值较小，大幅值梯度分布得少而离散。为了平衡梯度幅值与数量之间的关系，本文提出使用一个对数函数梯度进行映射：$${\bar{m}}_i=\{\begin{array}{ccc}\frac{1}{N}\log \left(\lambda \left(m_i-\delta \right)+1\right)& \text{ for }& m_i\ge \delta \\ 0& \text{ for }& m_i<\delta \end{array}$$其中，$N=\log (\lambda (1-\delta )+1)$，$m_i$是像素 $i$ 处的梯度幅值，可以看到当梯度小于阈值 $\delta$ 时，梯度幅值映射为零。$\lambda$是一个控制映射趋势的参数。${\bar{m}}_i$就代表梯度信息中和梯度幅值相关的部分，其输出控制在$0$到$1$。那么图像的曝光评价标准就定义为：$$M=\sum {\bar{m}}_i$$$M$越大说明曝光效果越好，图像中包含的信息越多。接下来说明如何进行曝光控制，在利用当前曝光时间获得的图像进行$\gamma$矫正，即$I_{out}=I_{in}^{\gamma }$，并求取最优的矫正值$\hat{\gamma }$：$$\hat{\gamma }=\arg \underset{\gamma }{\max }M\left(I_{in}^{\gamma }\right)$$具体操作是在$\gamma =\left[\frac{1}{1.9},1.9\right]$的范围里选取一些列的$\gamma$值对当前图像进行$\gamma$矫正，并计算矫正后的曝光程度$M$，然后利用五阶的多项式函数对这一系列离散值进行拟合，组中求得最优的矫正值$\hat{\gamma }$，如下图所示：获得最优矫正值$\hat{\gamma }$后通过更新函数就可以直接对曝光时间进行更新，更新函数分为线性更新函数和非线性更新函数：
线性更新函数：$$E_{t+1}=\left(1+\alpha K_p(1-\hat{\gamma })\right)E_t,\alpha =\{\begin{array}{ccc}1/2& \text{ for }& \hat{\gamma }\ge 1\\ 1& \text{ for }& \hat{\gamma }<1\end{array}$$非线性更新函数：$$\begin{array}{rl}{E}_{t+1}& =\left(1+\alpha K_p(R-1)\right)E_t\\ \text{ s.t. }R& =d\cdot \tan \left\{(2-\hat{\gamma })\cdot \arctan \left(\frac{1}{d}\right)-\arctan \left(\frac{1}{d}\right)\right\}+1\end{array}$$其中$E_t$是$t$时刻的曝光水平，更新的最终结果是使得最优矫正值$\hat{\gamma }$趋近与$1$，这样就完成了整个反馈的控制。在此基础上，这篇文章一个很重要的贡献是实现了多相机的联合自动曝光，这里简单介绍下：$$\begin{array}{rl}{E}_{t+1}^{i\ast }=& \underset{X}{\mathrm{argmin}}{\alpha }^i\cdot {\mathcal{E}}_u(i,t)+\frac{1-{\alpha }^i}{N}\sum _{j\in G(i)}{\mathcal{E}}_p(i,j,t)\\ \text{ s.t. }& {\mathcal{E}}_u(i,t)={\Vert X-E_{t+1}^i\Vert }^2\\ & {\mathcal{E}}_p(i,j,t)={\Vert X-r^{ij}\cdot E_t^{i\ast }\Vert }^2\\ & r^{ij}=\mathrm{median}\left(\frac{\mathrm{mean}\left(p^j\right)}{\mathrm{mean}\left(p^i\right)+ϵ}\right),p\in P\end{array}$$其中，优化函数将所需曝光量视为一元项${\mathcal{E}}_u(i,t)$，并将重叠区域中的亮度相似度作为成对项${\mathcal{E}}_p(i,j,t)$，$P$是两个相机之间的重叠区域，通过以上式为最优化目标进行优化操作就可以获得各个相机在联合自动曝光下最优曝光水平。

目前就看了这十篇左右的论文，看着看着又发现了近几年出的几篇很好的文章，是和SLAM相关的，考虑如何更好地将自动曝光算法和SLAM结合起来以提高系统的性能，很有意思。这篇博客就先写这么多，写得太长了自己都要看吐了，接下来把新的几篇论文看完再重新总结下，有问题欢迎交流~