链表面试常见考题（C++实现）

链表面试常见考题（C++实现）

常用方法：画图法

常用技巧：用于遍历搜索的游标 ListNode* cur; 用于返回值的哑节点 ListNode* dumny = new ,,

单链表更新先去考虑他的next指向问题。链表元素或者边界问题可以用前继节点pre、后继节点tail来进行判断。

1: 从尾到头打印单链表

解题思路：

从尾到头，利用栈先进后出的原理，使用栈数据结构遍历存放单链表的数据，之后出栈。

class Solution {
public:
    vector reversePrint(ListNode* head) {
        /* 根据返回值定义存储结果的变量 */
        vector result;
        /* 因为要反向输出值所以先把数据放入栈立里面然后在拿出来 */
        stack st;
        ListNode* cur = head;
        /* 将数据压入栈 */
        while(cur != NULL) {
            st.push(cur->val); // 单链表数据元素入栈
            cur = cur->next;
        }
        /* 将栈中的数据弹出 利用栈的性质可以反向输出结果 */
        while(!st.empty()) {
            result.push_back(st.top()); //将栈顶元素存放
            st.pop(); // 弹出栈顶元素
        }
        return result;

    }
};

2: 单链表实现约瑟夫环

约瑟夫环问题： 围坐在一张圆桌周围。从编号为k的人开始报数，数到m的那个人出列；他的下一个人又从1开始报数，数到m的那个人又出列；依此规律重复下去，直到圆桌周围的人全部出列。

思路：利用单链表数据结构，每次找到目标节点，之后将该节点从链表移除。更新当前的头节点，再次遍历寻找目标节点，之后剩下一个节点为止。

class solution
{
public:
    ListNode* YSF(ListNode* head, int m)
    {
        if (head == NULL) {
            return NULL;
        }
        
        ListNode* cur = NULL; // 游标
        while (head->next != head) { // 保证遍历到最后只剩一个最新的头节点
            for (int i = 0; i < m - 1; i++) {
                cur = head; // cur最后指向的是目标节点的前一个节点
                head = head->next; // head最后移动到了目标节点
            } 
            cur->next = head->next; // 目标节点从链表移除
            DeleteListNode(head); // 删除
            head = cur->next; // 头节点重新指向下一轮的第一个节点（cur->next就是）
        }
        
        return head;
    }

    void DeleteListNode(ListNode* node)
    {
        if (node == NULL) {
            return;
        }
        node->val = 0;
        node->next = NULL;
        free(node);
        node == NULL;
    }
};

3: 逆置/反转单链表

反转链表： 1 2 3 4 5  反转到 5 4 3 2 1。

思路： 单链表的反转，需要一个临时存储节点，用来记录反转前的链表指针指向的节点。否则反转完就不知道next是什么。同时需要一个新的pre节点告诉当前节点的前一个节点。最后返回最新的头结点。

class solution
{
public:
    ListNode* reverseNode(ListNode* head)
    {
        ListNode* tmp; // 定义一个存储节点，存放反转前的后继节点
        ListNode* cur = head; // 游标
        ListNode* pre; // 定义一个前继节点

        while(cur) {
            tmp = cur->next; // 存储后继节点
            cur->next = pre; // 反转
            pre = cur; // 前继节点更新
            cur = tmp; // 游标移动到下一个节点   
        }
            
        return pre; // pre最后指向了最新的头节点
    }

};

4: K个节点一组进行翻转

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

思路： 和第3题不同的是这个需要找到前继节点(pre)和后继节点(tail),之后在按照第3题进行类似的反转操作。本题目主要是移动后继结点实现反转。

class Solution
{
public:
    ListNode* reverseBetween(struct ListNode* head, int left, int right)
    {
        if (head == NULL) {
             return NULL; 
        }

        ListNode* cur = head; // 定义一个游标
        ListNode* pre = NULL; // 定义一个前继节点
        ListNode* tail = NULL; // 定义一个后继节点
        
        int gap = right - left + 1; //
        
        int i = 0;
        while(cur) {
            i++;
            // 1: find pre
            if (left >= 1 && i = left - 1) {
                pre = cur; // 当I移动到left的前一个，就找到了pre
            }
            
            // 2: find tail
            if (i > = left) {
                gap--; 
            }

            if (gap == 0) {
                tail = cur->next; 
                break;
            }

            // 3: 没找到tail,继续移动游标 cur
            cur = cur->next;

        }


        // start reverse
        cur = head;
        ListNode* tmp = NUll;
        int I = 0;
        gap = right - left + 1; // 反转的次数
        // 尾指针法
        while(cur) {
            i++;
            if (i >= left && gap > 0) {
                gap--;
                tmp = cur->next; // 存放后继节点
                cur->next = tail; // 反转，当前节点指向尾节点
                tail = cur; // 尾指针移动
                if (gap == 0) {
                    break; // 完成反转
                } else {
                    cur = tmp; // 移动游标，反转下一个节点 
                    continue;
                }

            }
            cur = cur->next;
        }
        
        if (left != 1) { // 
            pre->next = cur;
            return head;
        }

        return cur;
    }

};

5：单链表排序

链表 4 2 1 3 实现排序， 时间复杂度O(nlogn)， 空间复杂度O(1)

思路：利用归并排序， 自顶向下的排序。

归并排序： （1）找到链表的中点，以中点为分界，将链表拆分成两个子链表。寻找链表的中点可以使用快慢指针的做法，快指针每次移动 2步，慢指针每次移动 1步，当快指针到达链表末尾时，慢指针指向的链表节点即为链表的中间节点。

                   （2）根据中间递归拆分链表为子链表（最后拆分为最小单位，只有1个节点，头节点的next为tail）

                   （3）将拆分好的子链表 （两两合并），合并子链表时候，先判断小的节点，依靠游标将他们串联起来。

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        return SortList(head, nullptr);
    }

    ListNode* SortList(ListNode* head, ListNode* tail)
    {
        if (head == nullptr) {
            return nullptr;
        }

        if (head->next == tail) {
            head->next = nullptr;
            return head; // 只有一个节点， 返回本身就可以
        }

        ListNode* slow = head;  // 慢指针
        ListNode* fast = head;  // 快指针
        ListNode* mid =  nullptr;  // 中间节点

        while (fast != tail) { // 这里要注意，fast不能超出范围，保证块的，慢的就可以保证
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next; // 快指针移动两步
            }
        }

        mid = slow;
        return MergeList(SortList(head, mid), SortList(mid, tail)); // 递归去拆分寻找子链表的中间节点
    }

    ListNode* MergeList(ListNode* head1, ListNode* head2)  // 入参为两个要合并的子链表的头节点
    {
        ListNode* dumyNode = new ListNode(1);
        ListNode* cur = dumyNode;
        ListNode* tmp1 = head1;
        ListNode* tmp2 = head2;
        while (tmp1 && tmp2) {
            if (tmp1->val <= tmp2->val) {
                cur->next = tmp1;
                tmp1 = tmp1->next;
            } else {
                cur->next = tmp2;
                tmp2 = tmp2->next;
            }
            cur = cur->next;
        } 
        
        // 看谁还有剩余元素
        if (tmp1 != nullptr) {
            cur->next = tmp1;
        } else if (tmp2 != nullptr) {
            cur->next = tmp2;
        }

        cur = cur->next;
        cur->next = nullptr;
        return dumyNode->next;
    }

};

6： 寻找单链表的中间节点

思路： 只遍历一次的话，使用快慢指针。快指针每次移动 2步，慢指针每次移动 1步，当快指针到达链表末尾时，慢指针指向的链表节点即为链表的中间节点。不管是奇数偶数都可以。

class Solution
{
 public：
    ListNode* FindMidNode(ListNode* head)
    {
        if (head == nullptr) {
            return nullptr;
        }
        
        ListNode* tail = nullptr;
        
        if (head->next == tail) {
            head->next = nullptr;
            return head;
        }
    
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next;
            }
        }
        
        ListNode* mid = slow;
        return mid;
    }

};

7: 删除列表中倒数第K个节点 （一次遍历）

思路： 快慢指针

（1）快慢指针同时指向头节点

（2）快指针比慢指针先领先k步，之后再一起移动

（3）快慢指针一起移动，每次移动一步，当快指针超出链表，那么领先了k步，因此慢指针指向的链表节点就是倒数第K个节点。

class Solution {
public:
    ListNode* getKthFromEnd(ListNode* head, int k) {
        if (head == nullptr || k == 0) {
            return nullptr;
        } 

        ListNode* fast = head;
        ListNode* slow = head;
        
        int i = 0;
        while (i < k) {
            fast = fast->next;
            i++;
            if (i == k && fast == nullptr) {
                return slow;
            } else if (fast == nullptr) {
                return nullptr;
            }
        }
        
        ListNode* tail = nullptr;
        while (fast != tail) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;
    }
};

8：删除链表倒数第k个节点

思路： 先用快慢指针找到倒数第k个节点。找的时候定义一个指向目标节点的前继节点，用于后续的删除操作。（查找方法将题7）

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        if (head == nullptr) {
            return NULL;
        }

        ListNode* slow = head;
        ListNode* fast = head;
        ListNode* pre = nullptr; // 

        // 快速节点向前移动k步
        int i = 0;
        while (i < n) {
            fast = fast->next;
            i++;
            if (i == n && fast == nullptr) {
                return slow->next;
            } else if (fast == nullptr) {
                return slow;
            }
        }


        // 快慢指针移动寻找到倒数第k个节点 (slow锁指向的节点)
        ListNode* tail = nullptr;
        while (fast != tail) {
            pre = slow;
            slow = slow->next;
            fast = fast->next;
        }
        
        pre->next = slow->next;
        return head;
    }
};

9：判断链表是否带环？若带环，求环的长度？和入口点？

思路： 快慢指针，快指针比慢指针多走两步。当两者相遇说明有环。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if (head == NULL) {
            return false;
        }

        // 快慢指针
        ListNode* slow = head;
        ListNode* fast = head;

        ListNode* tail = nullptr;
        while(fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next; // 快指针移动两步
            } else {
                return false;
            }
            // 如果相遇则说明有环
            if (fast == slow) {
                return true;
            }
        }
        return false;
    }
};

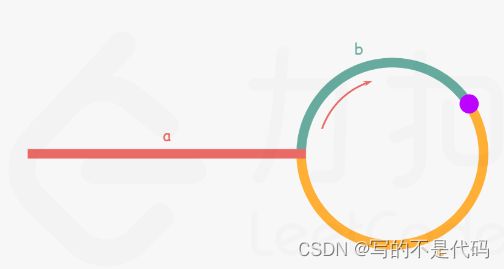
求解环的入口点：

思路：继续使用快慢指针，当快慢指针相遇的时候，快指针永远是慢指针的2倍。

a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)

块指针走了：a+(n+1)b+nc。 

慢指针走了： a+b 

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr) {
            return nullptr;
        }
        ListNode* slow = head;
        ListNode* fast = head;
        
        // 
        ListNode* pre = head;
        ListNode* tail = nullptr;
        while (fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next;
            } else {
                return nullptr;
            }
            if (slow == fast) {
                while (pre != slow) {
                    pre = pre->next;
                    slow = slow->next;
                }
                return pre;
            }
        }
        return nullptr;
    }

};

10： 合并两有序链表

思路： 创建一个哑节点，不断循环比较，让哑节点去指向两者小的一方，并且小的一方移动。

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        // 哑节点游标法，不需要创建新的节点
        ListNode* dunmy = new ListNode(-1); // 题目中没有head节点，需要我们自己创建一个哑节点
        ListNode* cur = dunmy; // 创建一个游标指向当前的哑节点

        // 遍历寻找
        while (l1 && l2) { // &&关系
            if  (l1->val < l2->val) {
                cur->next = l1; // 游标的指向
                l1 = l1->next;
            } else {
                cur->next = l2; // 游标的指向
                l2 = l2->next;
            }
            cur = cur->next; // 移动游标
        }

        // 寻找最后的剩余
        if (l1) {
            cur->next = l1;// 游标的指向
        } else {
            cur->next = l2;// 游标的指向
        }
        cur = cur->next;// 移动游标

        return dunmy->next;

    }
};

11： 旋转链表

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

思路： 先遍历整个链表，找到最后一个节点，并统计整个链表长度。

之后求出偏移（取余），找到旋转后的尾节点。修改链表头和尾的指向。

class Solution {
public:
    ListNode* rotateRight(ListNode* head, int k) {
        
        if (head == nullptr) 
            return nullptr;
        
        if (k == 0) 
            return head;
        
        // 计算链表长度, cur指向链表尾节点 
        ListNode *cur = head;
        int listLen = 0;
        while (cur->next) {
            cur = cur->next;
            listLen++;
        }
        listLen++;


        // 计算旋转分割节点
        int goStep = listLen - (k % listLen);

        // 求出新的尾节点
        ListNode *tail = head;
        int i = 1;
        while (i < goStep && tail) {
            tail = tail->next;
            i++;
        }

        // 进行旋转
        if (tail->next == nullptr) {
            return head;
        }

        ListNode* res = tail->next;
        tail->next = NULL;
        cur->next = head;
        return res;

    }
};