算法通关村 —— 原来滑动窗口如此简单

目录

原来滑动窗口如此简单

1. 滑动窗口基本思想

2. 两个入门题

2.1 子数组最大平均数

2.2 最长连续递增序列

---

原来滑动窗口如此简单

我们在数组和链表部分研究过双指针思想，这里我们继续学习滑动窗口思想。

滑动窗口其实是双指针思想的一种特殊场景，能够很好的解决一些特定场景的问题，因此就有了“滑动窗口思想”。

1. 滑动窗口基本思想

在数组双指针里，我们介绍过“对撞型”和“快慢型”两种方式，而滑动窗口思想其实就是快慢型的特例。
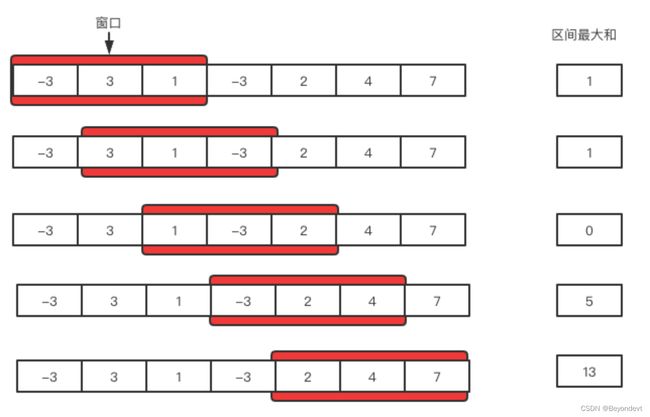
滑动窗口的思想非常简单，如下图所示，假如窗口的大小是3，当不断有新数据来时，我们会维护一个大小为3的一个区间，超过3的就将新的放入老的移走。有了区间，那我们就可以造题了，例如让你找序列上三个连续数字的最大和是多少或者了数组平均数是多少等等

从上面的图可以看到，窗口就是建立两个索引，left和right，并且保持{left,right}之间一共有3个元素，然后一边遍历序列，一边寻找，每改变一次就标记下当前区间的最大值。

这个例子已经告诉我们了什么是窗口、什么是窗口的滑动:

窗口: 窗口其实就是两个变量left和right之间的元素，也可以理解为一个区间。窗口大小可能固定，也可能变化，如果是固定大小的，那么自然要先确定窗口是否越界，再执行逻辑处理。如果不是固定的，就要先判断是否满足要求，再执行逻辑处理。
滑动: 说明这个窗口是移动的，事实上是left和right两个变量的移动，而不是序列中的元素。当变量移动的时，其中间的元素必然会发生变化，因此就有了这种不断滑动的效果。

在实际问题中，窗口大小不一定是固定的，我们可以思考两种场景：

1.固定窗口的滑动就是火车行驶这种大小不变的移动
2.可变的窗口就像两个老师带着一队学生外出，一个负责开路，一个负责断后，中间则是小朋友。两位老师之间的距离可能时大时小，但是整体窗口不断滑动。

根据窗口大小是否固定，可以造出两种类型的题
1.如果是固定的，则一般会让你求哪个窗口的元素最大、最小、平均值、和最大、和最小等等类型的问题
2.如果窗口是变的，则一般会让你求一个序列里最大、最小窗口是什么等等

滑动窗口题目本身没有太高的思维含量，但是实际在解题时候要注意以下几点:
1) 解题最终要落实到数组上，特别是边界处理上，稍有疏忽就难以得到准确的结果。
2) 有些元素的比较、判断等比较麻烦，不仅要借助集合等工具，而且处理过程中还有一些技巧，如果不熟悉会导致解题难度非常大。
3) 堆结构非常适合在流数据中找固定区间内的最大、最小等问题。因此滑动窗口经常和堆一起使用可以完美解决很多复杂的问题。

那双指针和滑动窗口啥区别呢? 滑动窗口是双指针的一种类型，主要关注两个指针之间元素的情况，因此范围更小一些，而双指针的应用范围更大，花样也更多。

2. 两个入门题

前面说到，根据滑动窗口大小变或者不变，有两种类型。以下就是两个基本的题目。

2.1 子数组最大平均数

给定 n 个整数，找出平均数最大且长度为 k 的连续数组，并输出该最大平均数。
其中 1<=k<=nums.length<=10^5。

输入: [1,12,-5,-6,50,3]， k = 4
输出: 12.75
解释: 最大平均数 (12-5-6+50)/4 = 51/4 = 12.75

这是典型的滑动窗口，大小固定了，就是K，那我们只要先读取k个，然后逐步让窗口向前走就可以了，每走一次就判断是否需要更新最大平均数，具体实现代码如下：

class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int len = nums.length;
        int windowSum = 0; // 纪录窗口的最大元素总和，最后再求最大平均数
        if(k > len || len < 1 || k < 1) return 0;
        // 先求第一个窗口，即前k个元素的和
        for(int i = 0; i < k; i++){
            windowSum += nums[i];
        }
        // 继续遍历，每次右边增加一个，左边减少一个，重新计算窗口最大和
        int res  = windowSum; // 记录历史窗口最大和
        for(int right = k; right < len; right++){
            windowSum += nums[right] - nums[right-k]; // 窗口右边增加一个，左边减少一个
            res = Math.max(res, windowSum); // 判断是否需要更新最大和
        }
        return (double)res / k;
    }
}

2.2 最长连续递增序列

我们再看一个窗户变化的情况。给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。

输入: nums =[1,3,5,4,7]
输出: 3
解释: 最长连续递增序列是 [1,3,5]，长度为3。

尽管[1,3,5,7] 也是升序的子序列，但它不是连续的，因为 5 和 7 在原数组里被4隔开。
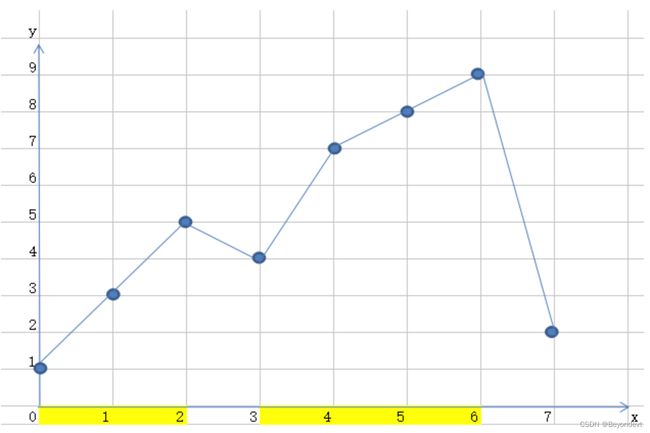
为了方便演示，我们将示例序列再增加几个元素{1,3,5,4,7,8,9,2}，则图示如下，题目要求找到最长的连续递增子序列。

由图可以清楚看到，最长递增子序列为(4,7,8,9)所以应该返回4。所以在遍历的时候，我们可以从第2个元素开始，先定义[left,right)的区间来表示当前的递增区间，执行如下操作:

⚪ 如果当前遍历到的元素比它左边的那一个元素要严格大，right就增加 。

⚪ 否则就将left跳到right的起始位置，重新开始计算。

具体实现代码如下：

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int left = 0, right = 0; // 窗口的左右指针
        int res = 0; // 存储最长递增序列长度
        while(right < nums.length){
            // 若右侧新元素比左侧小，则重新记录left位置
            if(right > 0 && nums[right - 1] >= nums[right]) left = right;
            right++; // 若比左侧大，则递增序列长度加1
            res = Math.max(res, right - left); // 判断是否需要更新最大长度
        }
        return res;
    }
}

上面代码中，序列在[left, right) 严格单调递增，区间的长度为right - left.

本题还有多种解法，另外一种简易的思路是一边遍历，一边统计每个递增区间的长度，如果长度超过之前所有区间的长度，就将其保留，代码如下:

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        // int left = 0, right = 0; // 窗口的左右指针
        // int res = 0; // 存储最长递增序列长度
        // while(right < nums.length){
        //     // 若右侧新元素比左侧小，则重新记录left位置
        //     if(right > 0 && nums[right - 1] >= nums[right]) left = right;
        //     right++; // 若比左侧大，则递增序列长度加1
        //     res = Math.max(res, right - left); // 判断是否需要更新最大长度
        // }
        // return res;
        int curLen = 1; // 当前连续递增区间的长度
        int res = 1; // 存储最大递增区间长度
        for (int i = 1; i < nums.length; i++){
            if(nums[i - 1] >= nums[i]){
                // 若右侧新元素比左侧小，则重新记录当前连续递增区间长度
                curLen = 1;
            }else{
                curLen++; // 若比左侧大，则当前递增序列长度加1
            }
            res = Math.max(res, curLen); // 判断是否需要更新最大长度
        }
        return res;
    }
}