自动驾驶车辆轨迹跟踪
相对于传统的模型预测控制(MPC),简化的车辆模型通常会导致预测结果不准确,这对车辆的转弯等行为具有负面影响。因此作者提出了一种轨迹规划和跟踪框架:
- 该框架应用人工势场来获得目标轨迹;
- 并利用具有PID反馈的MPC来有效跟踪规划的轨迹;
来自:Trajectory Tracking of Autonomous Vehicle Based on Model Predictive Control With PID Feedback
目录
- 问题描述
- 方法
-
- 人工势场
-
- 道路环境势场
- 周边车辆势场
- 驾驶方向势场
- 车辆轨迹规划
- 跟踪控制器设计
-
- 车辆运动模型
- 模型预测控制的设计
- 反馈控制的设计
- 横向设计轨迹的修正
问题描述
自动驾驶的轨迹规划方法包括人工势场,快速探索随机树等。人工势场结构简单,数学描述清晰,是目前常用的轨迹规划方法。在完成轨迹规划后,由于轨迹会随着周围环境的变化而变化,因此实时跟踪轨迹也是重要的。一般来说,跟踪控制算法分为两类:基于数据的控制和基于模型的控制:
- 数据驱动的控制体系结构简单,没有车辆的动态和运动学模型,但是如果没有合适的参数,控制车辆的运动将出现振动等不稳定情况,此外,这类方法的可扩展性和物理可解释性都很差;
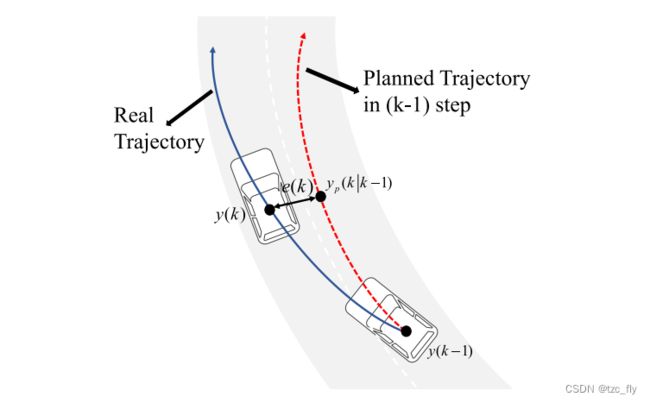
- 基于模型的控制方法根据车辆的运动学模型产生控制值,基于模型的控制器可以减少调优所需的工作量,然而,这些基于模型的控制算法需要高精度的运动或动态车辆模型,这在实际车辆控制中是不可能实现的。通常,真实的自动驾驶车辆采用过于简化的运动学或动力学车辆模型。在车辆通过长曲线时,会出现与车道线的巨大偏差,如图1。
该研究对人工势场和控制方法进行了改进,首先是对势场进行改进,消除了自动驾驶车辆与障碍车辆,道路边缘之间的局部极小值。其次,提出基于动态和跟踪特性的反馈MPC控制方法。MPC代表了车辆的运动特性,PID的反馈可以提高跟踪性能。对于传统的MPC来说,内部模型和真实车辆之间的差距是不可避免的。在这种情况下,PID方法可以减少由近似模型引起的误差,MPC方法可以减少控制器整定和校准的时间和精力。
- 图1:自动驾驶车辆的规划轨迹和实际轨迹之间的误差。
方法
人工势场
势场通常由“碗状”吸引场和“山状”排斥场组成。在这种情况下,前者迫使对象靠近,后者迫使对象朝相反方向移动。该研究采用势场来规划车辆的轨迹。道路运输中势场的类型大致分为两类:道路环境势场和周边车辆势场。
道路环境势场
道路环境势场一般考虑道路边缘和车道线,公式1和公式2表示道路边缘和车道线的势场,公式3为道路环境势场。

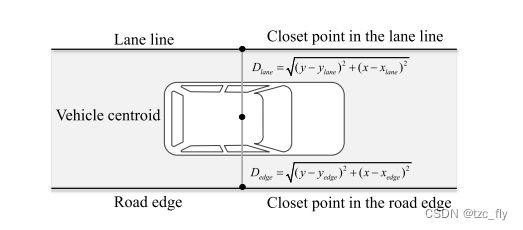
其中, A e d g e A_{edge} Aedge和 A l a n e A_{lane} Alane分别为道路边缘和车道线的势场系数,由它们的势场方向和自身车辆的最大横向速度确定。 σ l a n e \sigma_{lane} σlane为车道线势场的衰减系数,该常数反映了 U l a n e U_{lane} Ulane的衰减率,从而保证在车道中间位置处的 U r o a d = 0 U_{road}=0 Uroad=0。如图2所示, D e d g e D_{edge} Dedge为自动驾驶车辆到道路边缘的最短距离, D l a n e D_{lane} Dlane为自动驾驶车辆到道路车道线的最短长度。
- 图2:在道路环境的人工势场建模中使用的自动驾驶车辆距离示意图。
周边车辆势场
- 图3:障碍车辆的人工势场建模示意图。
该研究还考虑了局部车道上前面的障碍车辆,并假设自动驾驶车辆的移动速度比周边车辆快。在这种情况下,障碍车辆的势场建模是在原点固定在车身框架末端中点的坐标系中实现的。如图3所示,在障碍车辆周围,直角梯形区域是障碍车辆的安全区域。注意,靠近道路边缘的一侧比靠近车道线的一侧长。如果障碍车辆在中间车道,将使用传统的等腰三角形场。 S S S是障碍车辆的安全距离。该安全距离由自动驾驶车辆和障碍车辆之间的相对速度 v r e v_{re} vre确定。
![]()
其中, K s K_{s} Ks为反应时间的系数, S m i n S_{min} Smin为最小安全距离,当自动驾驶车辆位于图3中的位置 P 1 P1 P1时,纵向和横向势场值如公式5和公式6所示。
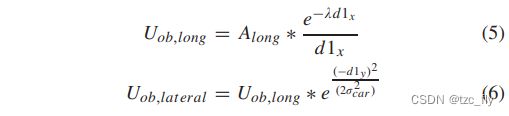
其中, d 1 x d1_{x} d1x和 d 1 y d1_{y} d1y为在障碍车辆坐标系的 x x x轴方向和 y y y轴方向上从 d 1 d1 d1除以的距离。 d 1 d1 d1是从 p 1 p1 p1到障碍车辆的安全区域的最短距离值。 λ , σ c a r \lambda,\sigma_{car} λ,σcar是反应衰减率的纵向和横向势场的衰减系数,可以通过人类驾驶行为进行校准。 A l o n g A_{long} Along是纵向势场系数,表示由于前方障碍物车辆造成的最大纵向局部速度。当自动驾驶车辆位于位置 P 2 P2 P2时,纵向势场设置为 A l o n g A_{long} Along,横向势场如公式7所示。
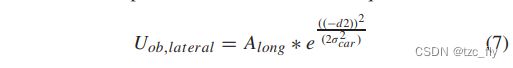
其中 d 2 d2 d2是从 P 2 P2 P2到安全区域的最短距离值。当自动驾驶车辆位于位置 P 3 P3 P3时,纵向势场显示如下。
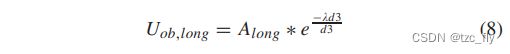
其中 d 3 d3 d3是从 P 3 P3 P3到安全区域的最短距离值。当自动驾驶车辆处于位置 P 4 P4 P4时,纵向人工势场被设置为 A l o n g A_{long} Along。
驾驶方向势场
为了保持车辆的前进,假设自动驾驶车辆的前进方向有一个势场,该势场可以诱导车辆的前进趋势。如公式9所示,吸引势场 U a t t U_{att} Uatt是设计速度 v d v_d vd的函数,如下所示。
![]()
其中 k k k和 τ τ τ是吸引势场系数, k k k为正, τ τ τ为负。
车辆轨迹规划
如上所述,在纵向方向上,有吸引势场 U a t t U_{att} Uatt和纵向障碍势场 U o b , l o n g U_{ob,long} Uob,long。此外,在横向方向上,有道路车道势场 U l a n e U_{lane} Ulane、道路边缘势场 U e d g e U_{edge} Uedge和横向障碍物势场 U o b , l a t e r a l U_{ob,lateral} Uob,lateral。随后,自动驾驶车辆的总纵向 U x U_{x} Ux和横向 U y U_y Uy势场值如式10和式11所示。
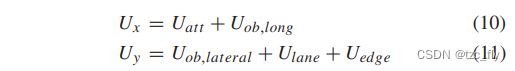
基于总势场,开始执行局部轨迹规划,如公式12和公式13所示。位置序列 [ ( x p , t ( 1 ) , y p , t ( 1 ) ) , ( x p , t ( 2 ) , y p , t ( 2 ) ) , . . . , ( x p , t ( N ) , y p , t ( N ) ) ] [(x_{p,t}(1),y_{p,t}(1)),(x_{p,t}(2),y_{p,t}(2)),...,(x_{p,t}(N),y_{p,t}(N))] [(xp,t(1),yp,t(1)),(xp,t(2),yp,t(2)),...,(xp,t(N),yp,t(N))]形成自动驾驶车辆在时刻 t t t的局部规划轨迹。
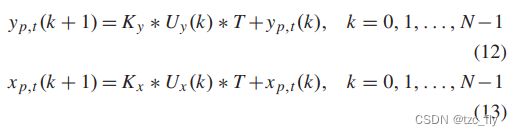
其中, ( x p , t ( 0 ) , y p , t ( 0 ) ) (x_{p,t}(0),y_{p,t}(0)) (xp,t(0),yp,t(0))为自动驾驶车辆在时刻 t t t的位置。 ( x p , t ( k + 1 ) , y p , t ( k + 1 ) ) (x_{p,t}(k+1),y_{p,t}(k+1)) (xp,t(k+1),yp,t(k+1))为车辆在时刻 ( t + ( k + 1 ) T ) (t+(k+1)T) (t+(k+1)T)上的计划位置。 K y K_{y} Ky和 K x K_{x} Kx是速度因子,确保 K y U y ( k ) K_{y}U_{y}(k) KyUy(k)小于最大横向速度, K x U x ( k ) K_{x}U_{x}(k) KxUx(k)小于最大纵向速度。
跟踪控制器设计
关于横向控制(车轮转向角 σ t σ_t σt),MPC提供前馈控制律,PID应用反馈控制律(PID_lat)。在纵向控制(车辆节气门位置 T k T_k Tk)方面,MPC控制器作为辅助纵向规划器,产生速度分布。此外,自动驾驶车辆通过PID控制器(PID_long)跟踪速度曲线。图4展示了具有PID反馈的MPC控制器的结构。
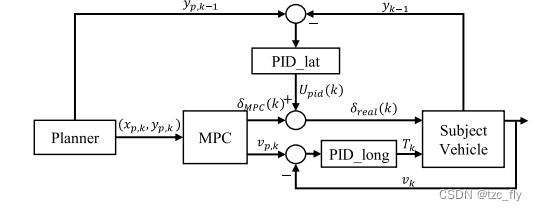
- 图4:具有PID反馈的MPC控制器的结构。
车辆运动模型
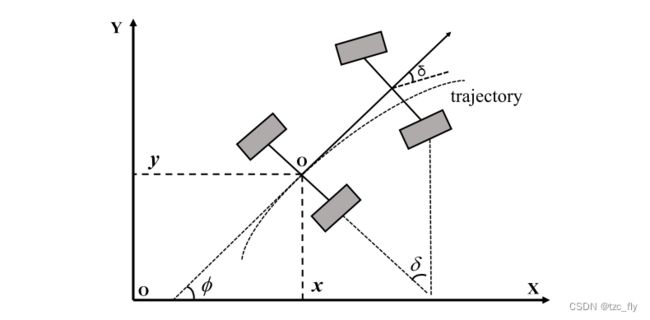
- 图5:车辆运动模型
将纵向、横向和偏航运动的线性运动学模型应用于MPC控制器。如图5所示, x , y x,y x,y为车辆后桥在惯性坐标上的中点位置。其中, ϕ \phi ϕ是车辆的方向。我们定义一个有状态变量的线性系统 X = [ x , y , ϕ ] T X=[x,y,\phi]^{T} X=[x,y,ϕ]T和控制变量 u = [ v , δ ] T u=[v,\delta]^{T} u=[v,δ]T,得到相应的3-DOF车辆动力学模型如下所示。
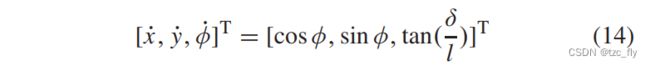
这些微分方程可以写成下面的紧凑形式。

设计轨迹可定义如下:
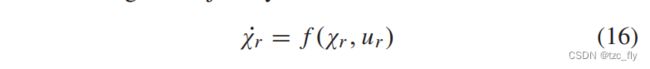
其中 χ r χr χr为参考状态, u r u_r ur为参考控制输出。基于对设计点的泰勒级数展开,我们得到近似如下:

结合公式16和17得到:
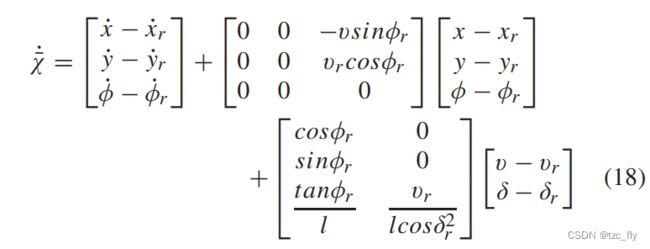
式中 x r x_r xr、 y r y_r yr、 ϕ r \phi_r ϕr分别为参考 x x x轴位置、参考 y y y轴位置和参考航向角, v r v_r vr和 δ r δ_r δr是参考速度和参考前轮角。对周期为 T T T的公式18中的系统离散化:

为了形成增广模型,选择一个新的状态变量:

其中 m m m和 n n n为状态变量和控制变量的维数。 Δ u ( k ∣ t ) \Delta u(k|t) Δu(k∣t)是控制增量。
模型预测控制的设计
假设 A ‾ k , t = A ‾ t , t , B ‾ k , t = B ‾ t , t \overline{A}_{k,t}=\overline{A}_{t,t},\overline{B}_{k,t}=\overline{B}_{t,t} Ak,t=At,t,Bk,t=Bt,t,基于状态空间 ( A ‾ k , t , B ‾ k , t , C ‾ k , t ) (\overline{A}_{k,t},\overline{B}_{k,t},\overline{C}_{k,t}) (Ak,t,Bk,t,Ck,t),使用未来控制参数集依次计算预测状态变量:
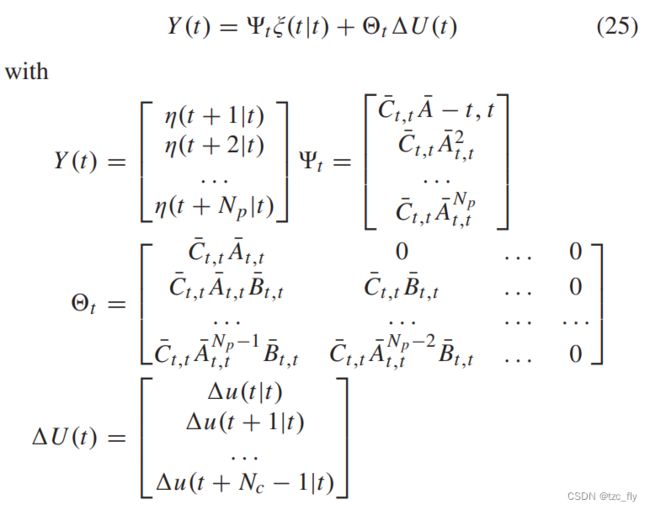
对于协同控制系统中主体车辆的纵向和横向运动控制,我们定义如下的代价函数:
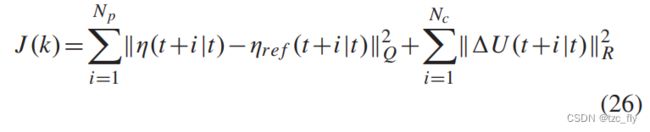
其中第一项与最小化预测输出点与期望轨迹点之间的误差的目标有关,第二项反映了对 Δ U ( t ) \Delta U(t) ΔU(t)大小的考虑。为了找到最优的 Δ U \Delta U ΔU,我们最小化 J J J,它可以表示为:
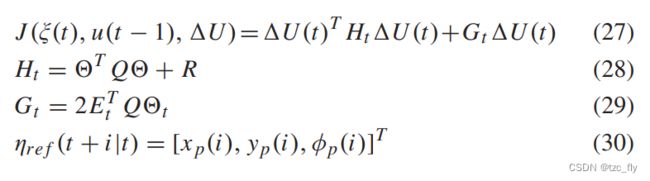
反馈控制的设计
如图3所示,横向控制由MPC前馈控制器和PID反馈控制器(PID_lat)组成。如前面所分析的,MPC中简化的车辆模型可能会产生误差。在仿真实验中,传统MPC试图跟踪计划轨迹。通过弯道时车辆协调横向误差大部分集中在0.035 ~ 0.082范围内。这种误差是由于MPC中车辆内部模型的不准确造成的。因此,PID_lat控制律足以补偿,引入PID_lat控制律对MPC控制器产生校正,如式32所示。最后,公式33表明,产生最终横向控制值 δ r e a l ( k ) δ_{real}(k) δreal(k)的两个部分是MPC控制值 δ M P C ( k ) δ_{MPC}(k) δMPC(k)和PID_lat控制值 U p i d ( k ) U_{pid}(k) Upid(k)。
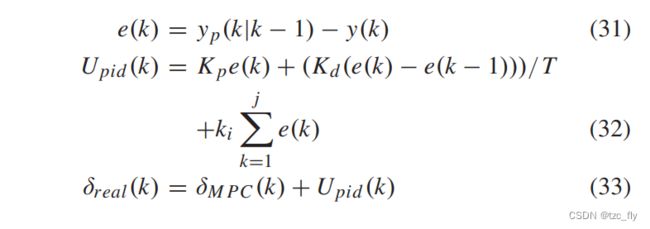
横向设计轨迹的修正
纵向跟踪误差可能会发生,特别是在车辆的初始运动阶段。在这种情况下,对于时间 ( t = k ) (t = k) (t=k),最近的设计轨迹点是 ( x p ( k ) , y p ( k ) ) (x_p (k), y_p(k)) (xp(k),yp(k)),而不是前面序列中假定的点 ( x p ( k + 1 ) , y p ( k + 1 ) ) (x_p (k + 1), y_p(k + 1)) (xp(k+1),yp(k+1))。此外,以点 ( x p ( k + 1 ) , y p ( k + 1 ) ) (x_p(k + 1), y_p(k + 1)) (xp(k+1),yp(k+1))为目标的横向控制将导致横向运动的简化,并与设计轨迹相比产生横向误差。
这种扭曲的轨迹可能会导致碰撞风险,如图6所示。在这种情况下,对车辆 ( t = k ) (t = k) (t=k)的控制瞄准其原始目标点 ( x d ( k + 1 ) , y d ( k + 1 ) ) (x_d (k + 1), y_d (k + 1)) (xd(k+1),yd(k+1))可能导致与障碍车辆发生碰撞。为了消除这种简化,可以解耦横向和纵向目标点。对于时间 t = k t = k t=k,纵向目标点 x d ( k + 1 ) x_d (k + 1) xd(k+1)保持不变,横向目标点需要修改。选择最接近前面序列中当前位置的目标点作为修改后的横向目标,用 y d ∗ ( k + 1 ) y^*_d (k + 1) yd∗(k+1)表示。也就是说,控制器中实际使用的目标点为 ( x d ( k + 1 ) , y d ∗ ( k + 1 ) ) (x_d (k + 1),y^*_d (k + 1)) (xd(k+1),yd∗(k+1)),时刻 k k k的目标点为 ( x d ( k + 1 ) , y d ( k ) ) (x_d (k + 1),y_d (k )) (xd(k+1),yd(k))

- 图6:由扭曲的轨迹引起碰撞。