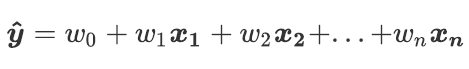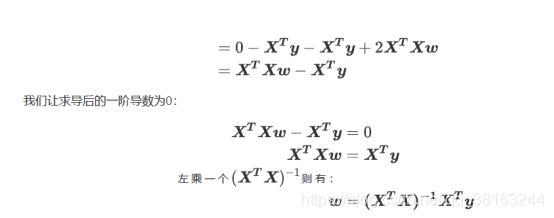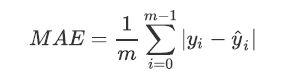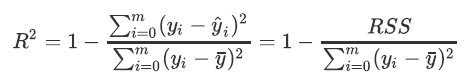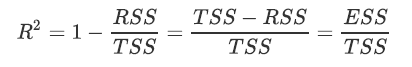使用sklearn库学习线性回归（一）

 

目录

1，概述

1.1，判别式方法

1.2，线性回归介绍

1.3，sklearn中的线性回归

2，多元线性回归LinearRegression

2.1，多元线性回归的基本原理

2.2，最小二乘法求解多元线性回归的参数

2.3，linear_model.LinearRegression

2.3.1，案例演示

3，回归类的模型评估指标

3.1，是否预测了正确的数值

3.2，是否拟合了足够的信息

---

1，概述

1.1，判别式方法

• 产生式模型需要计算输入输出的联合概率
  • 需要知道（or 假定）样本的概率分布
    • 定义似然密度的隐式参数
    • 为没给类别搜索最大化样本似然的参数
  • 也称为基于似然的分类（Likelihood-based Classification）
• 判别式模型直接构造（假定）判别式
  • 。
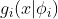  • 判别式的显式参数（特征变量的权重）。
• 判别式方法
  • 基于似然的方法关注类区域中的概率密度
  • 基于判别式的方法只关注类区域之间的边界。

1.2，线性回归介绍

回归是一种应用广泛的预测建模技术，这种技术的核心在于预测的结果是连续型变量。决策树，随机森林，支持向量机的分类器等分类算法的预测标签是分类变量，多以{0，1}来表示，而无监督学习算法比如PCA，KMeans并不求解标签。回归需求在现实中非常多，所以我们自然也有各种各样的回归类算法。最著名的就是我们的线性回归和逻辑回归，从他们衍生出了岭回归，Lasso，弹性网，除此之外，还有众多分类算法改进后的回归，比如回归树，随机森林的回归，支持向量回归，贝叶斯回归等等。

回归类算法的数学相对简单，通常，理解线性回归可以有两种角度：矩阵的角度和代数的角度。几乎所有机器学习的教材都是从代数的角度来理解线性回归的，类似于我们在逻辑回归和支持向量机中做的那样，将求解参数的问题转化为一个带条件的最优化问题，然后使用三维图像让大家理解求极值的过程。

1.3，sklearn中的线性回归

sklearn中的线性模型模块是linear_model，在学习逻辑回归的时候提到过这个模块。linear_model包含了多种多样的类和函数，其中逻辑回归相关的类和函数在这里就不给大家列举了。

类/函数	说明
普通线性回归	使用普通最小二乘法的线性回归，转化为求解最值问题
linear_model.LinearRegression
岭回归	岭回归，一种将L2作为正则化工具的线性最小二乘回归（均方误差作为惩罚项）
linear_model.Ridge
linear_model.RidgeCV	带交叉验证的岭回归
linear_model.RidgeClassifier	岭回归的分类器
linear_model.RidgeClassifierCV	带交叉验证的岭回归的分类器
linear_model.ridge_regression	【函数】用正太方程法求解岭回归
LASSO
linear_model.Lasso	Lasso，使用L1作为正则化工具来训练的线性回归模型
linear_model.LassoCV	带交叉验证和正则化迭代路径的Lasso
linear_model.LassoLars	使用最小角度回归求解的Lasso
linear_model.LassoLarsCV	带交叉验证的使用最小角度回归求解的Lasso
linear_model.LassoLarsIC	使用BIC或AIC进行模型选择的，使用最小角度回归求解的Lasso
linear_model.MultiTaskLasso	使用L1 / L2混合范数作为正则化工具训练的多标签Lasso
linear_model.MultiTaskLassoCV	使用L1 / L2混合范数作为正则化工具训练的，带交叉验证的多标签Lasso
linear_model.lasso_path	【函数】用坐标下降计算Lasso路径
弹性网
linear_model.ElasticNet	弹性网，一种将L1和L2组合作为正则化工具的线性回归
linear_model.ElasticNetCV	带交叉验证和正则化迭代路径的弹性网
linear_model.MultiTaskElasticNet	多标签弹性网
linear_model.MultiTaskElasticNetCV	带交叉验证的多标签弹性网
linear_model.enet_path	【函数】用坐标下降法计算弹性网的路径
最小角度回归
linear_model.Lars	最小角度回归（Least Angle Regression，LAR）
linear_model.LarsCV	带交叉验证的最小角度回归模型
linear_model.lars_path	【函数】使用LARS算法计算最小角度回归路径或Lasso的路径
正交匹配追踪
linear_model.OrthogonalMatchingPursuit	正交匹配追踪模型（OMP）
linear_model.OrthogonalMatchingPursuitCV	交叉验证的正交匹配追踪模型（OMP）
linear_model.orthogonal_mp	【函数】正交匹配追踪（OMP）
linear_model.orthogonal_mp_gram	【函数】Gram正交匹配追踪（OMP）
贝叶斯回归
linear_model.ARDRegression	贝叶斯ARD回归。ARD是自动相关性确定回归（Automatic Relevance Determination Regression），是一种类似于最小二乘的，用来计算参数向量的数学方法。
linear_model.BayesianRidge	贝叶斯岭回归
其他回归
linear_model.PassiveAggressiveClassifier	被动攻击性分类器
linear_model.PassiveAggressiveRegressor	被动攻击性回归
linear_model.Perceptron	感知机
linear_model.RANSACRegressor	RANSAC（RANdom SAmple Consensus）算法。
linear_model.HuberRegressor	胡博回归，对异常值具有鲁棒性的一种线性回归模型
linear_model.SGDRegressor	通过最小化SGD的正则化损失函数来拟合线性模型
linear_model.TheilSenRegressor	Theil-Sen估计器，一种鲁棒的多元回归模型

2，多元线性回归LinearRegression

2.1，多元线性回归的基本原理

线性回归是机器学习中最简单的回归算法，多元线性回归指的就是一个样本有多个特征的线性回归问题。对于一个有个特征的样本而言，它的回归结果可以写作一个几乎人人熟悉的方程：

被统称为模型的参数，其中被称为截距(intercept)，被称为回归系数(regression coefficient)，有时也是使用或者来表示。这个表达式，其实就和我们小学时就无比熟悉的是同样的性质。其中是我们的目标变量，也就是标签。是样本上的特征不同特征。如果考虑我们有m个样本，则回归结果可以被写作： 

其中是包含了m个全部的样本的回归结果的列向量。注意，我们通常使用粗体的小写字母来表示列向量，粗体的大写字母表示矩阵或者行列式。我们可以使用矩阵来表示这个方程，其中可以被看做是一个结构为(n+1,1)的列矩阵，是一个结构为(m,n+1)的特征矩阵，则有：

线性回归的任务，就是构造一个预测函数来映射输入的特征矩阵和标签值的线性关系，这个预测函数在不同的教材上写法不同，可能写作， ，或者等等形式，但无论如何，这个预测函数的本质就是我们需要构建的模型，而构造预测函数的核心就是找出模型的参数向量。但我们怎样才能够求解出参数向量呢？

记得在逻辑回归和SVM中，我们都是先定义了损失函数，然后通过最小化损失函数或损失函数的某种变化来将求解参数向量，以此将单纯的求解问题转化为一个最优化问题。在多元线性回归中，我们的损失函数如下定义：

其中是样本对应的真实标签，帽 也就是是样本在一组参数下的预测标签。

首先，这个损失函数代表了向量帽的L2范式的平方结果，L2范式的本质是就是欧式距离，即是两个向量上的每个点对应相减后的平方和再开平方，我们现在只实现了向量上每个点对应相减后的平方和，并没有开方，所以我们的损失函数是L2范式，即欧式距离的平方结果。

在这个平方结果下，我们的和帽分别是我们的真实标签和预测值，也就是说，这个损失函数实在计算我们的真实标签和预测值之间的距离。因此，我们认为这个损失函数衡量了我们构造的模型的预测结果和真实标签的差异，因此我们固然希望我们的预测结果和真实值差异越小越好。所以我们的求解目标就可以转化成：

其中右下角的2表示向量的L2范式，也就是我们的损失函数所代表的含义。在L2范式上开平方，就是我们的损失函数。这个式子，也正是sklearn当中，用在类Linear_model.LinerRegression背后使用的损失函数。我们往往称呼这个式子为SSE（Sum of Sqaured Error，误差平方和）或者RSS（Residual Sum of Squares 残差平方和）。在sklearn所有官方文档和网页上，我们都称之为RSS残差平方和。

2.2，最小二乘法求解多元线性回归的参数

现在问题转换成了求解让RSS最小化的参数向量，这种通过最小化真实值和预测值之间的RSS来求解参数的方法叫做最小二乘法。求解极值的第一步往往是求解一阶导数并让一阶导数等于0，最小二乘法也不能免俗。因此，我们现在残差平方和RSS上对参数向量求导。这里的过程涉及到少数矩阵求导的内容，需要查表来确定。

 

 

到了这里，我们希望能够将留在等式的左边，其他与特征矩阵有关的部分都放到等式的右边，如此就可以求出的最优解了。这个功能非常容易实现，只需要我们左乘的逆矩阵就可以。在这里，逆矩阵存在的充分必要条件是特征矩阵不存在多重共线性。假设矩阵的逆是存在的，此时我们的就是我们参数的最优解。求解出这个参数向量，我们就解出了我们的，也就能够计算出我们的预测值帽了。

除了多元线性回归的推导之外，这里还需要提到一些在上面的推导过程中不曾被体现出来的问题。在统计学中，使用最小二乘法来求解线性回归的方法是一种”无偏估计“的方法，这种无偏估计要求因变量，也就是标签的分布必须服从正态分布。这是说，我们的y必须经由正太化处理（比如说取对数，或者使用在《数据预处理与特征工程》中提到的类QuantileTransformer或者PowerTransformer）。在机器学习中，我们会先考虑模型的效果，如果模型效果不好，那我们可能考虑改变因变量的分布。

2.3，linear_model.LinearRegression

class sklearn.linear_model.LinearRegression (fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)

参数	含义
fit_intercept	布尔值，可不填，默认为True是否计算此模型的截距。如果设置为False，则不会计算截距
normalize	布尔值，可不填，默认为False 当fit_intercept设置为False时，将忽略此参数。如果为True，则特征矩阵X在进入回归之前将会被减去均值（中心化）并除以L2范式（缩放）。如果你希望进行标准化，请在fit数据之前用preprocessing模块中的标准化专用类StandardScaler
copy_X	布尔值，可不填，默认为True 如果为真，将在X.copy()上进行操作，否则的话原本的特征矩阵X可能被线性回归影响并覆盖
n_jobs	整数或者None，可不填，默认为None 用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在joblib.parallel_backend上下文中，否则None统一表示为1。如果输入 -1，则表示使用全部的CPU来进行计算。

线性回归的类可能是我目前为止学到的最简单的类，仅有四个参数就可以完成一个完整的算法。并且看得出，这些参数中并没有一个是必填的，更没有对我们的模型有不可替代作用的参数。这说明，线性回归的性能，往往取决于数据本身，而并非是我们的调参能力，线性回归也因此对数据有着很高的要求。幸运的是，现实中大部分连续型变量之间，都存在着或多或少的线性联系。所以线性回归虽然简单，却很强大。顺便一提，sklearn中的线性回归可以处理多标签问题，只需要在fit的时候输入多维度标签就可以了。

2.3.1，案例演示

from sklearn.linear_model import LinearRegression as LR
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing as fch #加利福尼亚房屋价值数据集
import pandas as pd

housevalue=fch()
X=pd.DataFrame(housevalue.data)
y=housevalue.target

housevalue.target_names
housevalue.feature_names

X.columns=housevalue.feature_names
# 把特征矩阵的列名修改为属性名字

# 划分数据
xtrain,xtest,ytrain,ytest=train_test_split(X,y,test_size=0.3,random_state=420)

# 恢复划分数据后的索引
for i in [xtrain,xtest]:
    i.index=range(i.shape[0])

# 在现实情况中，必须先分训练集和测试集，然后重新编索引，最后对数据进行标准化
# 先用训练集训练（fit）标准化的类，然后用训练好的类分别转化(transform)训练集和测试集

# 实例化模型并且拟合模型
lr=LR().fit(xtrain,ytrain)
# lr就是我们训练好的对象（模型）

# 使用predict接口对我们的y进行预测
yhat=lr.predict(xtest)

yhat.max()
# 我们的数据集最大值是5左右，但是现在拟合数据的最大值达到7，所以说我们的拟合效果不是很好。

# 查看我们建立好的方程的系数向量w,也就是斜率
lr.coef_
# 一共有8个w，每一个特征对应于一个系数

# 查看我们的截距w0,截距只有一个
lr.intercept_

[*zip(xtrain.columns,lr.coef_)]

•  属性说明

属性	含义
coef_	数组，形状为 (n_features, )或者(n_targets, n_features) 线性回归方程中估计出的系数。如果在fit中传递多个标签（当y为二维或以上的时候），则返回的系数是形状为（n_targets，n_features）的二维数组，而如果仅传递一个标签，则返回的系数是长度为n_features的一维数组
intercept_	数组，线性回归中的截距项。

3，回归类的模型评估指标

回归类算法的模型评估一直都是回归算法中的一个难点，但不像我们曾经讲过的无监督学习算法中的轮廓系数等等评估指标，回归类与分类型算法的模型评估其实是相似的法则——找真实标签和预测值的差异。只不过在分类型算法中，这个差异只有一种角度来评判，那就是是否预测到了正确的分类，而在我们的回归类算法中，我们有两种不同的角度来看待回归的效果：

• 第一，我们是否预测到了正确的数值。
• 第二，我们是否拟合到了足够的信息。

这两种角度，分别对应着不同的模型评估指标。

3.1，是否预测了正确的数值

回忆一下我们的RSS残差平方和，它的本质是我们的预测值与真实值之间的差异，也就是从第一种角度来评估我们回归的效力，所以RSS既是我们的损失函数，也是我们回归类模型的模型评估指标之一。但是，RSS有着致命的缺点：它是一个无界的和，可以无限地大。我们只知道，我们想要求解最小的RSS，从RSS的公式来看，它不能为负，所以RSS越接近0越好，但我们没有一个概念，究竟多小才算好，多接近0才算好？为了应对这种状况，sklearn中使用RSS的变体，均方误差MSE（mean squared error）来衡量我们的预测值和真实值的差异：

均方误差，本质是在RSS的基础上除以了样本总量，得到了每个样本量上的平均误差。有了平均误差，我们就可以将平均误差和我们的标签的取值范围在一起比较，以此获得一个较为可靠的评估依据。在sklearn当中，我们有两种方式调用这个评估指标，一种是使用sklearn专用的模型评估模块metrics里的类mean_squared_error，另一种是调用交叉验证的类cross_val_score并使用里面的scoring参数来设置使用均方误差。

# 回归类的模型评估指标
# 使用均方误差进行评估
from sklearn.metrics import mean_squared_error as MSE
# 使用预测出来的值和真实的值作为参数
MSE(yhat,ytest)
# 发现有0.5左右的误差

# 查看真实值的均值
ytest.mean()
# 发现平均均方误差和test数据集的均值相差很大

# 使用我们的交叉验证进行评估
cross_val_score(lr,X,y,cv=10,scoring='neg_mean_squared_error')
# 10组交叉验证，所以出现了10个结果
# 这个是负值均方误差，如果想要得到均方误差，前面*-1即可
# 只要使用scoring参数求误差，就必须写负均方误差

# 使用下面scoring的参数会报错
cross_val_score(lr,X,y,cv=10,scoring="mean_squared_error")
#为什么报错了？来试试看！
import sklearn
sorted(sklearn.metrics.SCORERS.keys())

• 均方误差为负。

我们在决策树和随机森林中都提到过，虽然均方误差永远为正，但是sklearn中的参数scoring下，均方误差作为评判标准时，却是计算”负均方误差“（neg_mean_squared_error）。这是因为sklearn在计算模型评估指标的时候，会考虑指标本身的性质，均方误差本身是一种误差，所以被sklearn划分为模型的一种损失(loss)。在sklearn当中，所有的损失都使用负数表示，因此均方误差也被显示为负数了。真正的均方误差MSE的数值，其实就是neg_mean_squared_error去掉负号的数字。

• 除了MSE，我们还有与MSE类似的MAE（Mean absolute error，绝对均值误差）：

其表达的概念与均方误差完全一致，不过在真实标签和预测值之间的差异外我们使用的是L1范式（绝对值）。现实使用中，MSE和MAE选一个来使用就好了。在sklearn当中，我们使用命令from sklearn.metrics import mean_absolute_error来调用MAE，同时，我们也可以使用交叉验证中的scoring = "neg_mean_absolute_error"，以此在交叉验证时调用MAE。 

3.2，是否拟合了足够的信息

对于回归类算法而言，只探索数据预测是否准确是不足够的。除了数据本身的数值大小之外，我们还希望我们的模型能够捕捉到数据的”规律“，比如数据的分布规律，单调性等等，而是否捕获了这些信息并无法使用MSE来衡量。

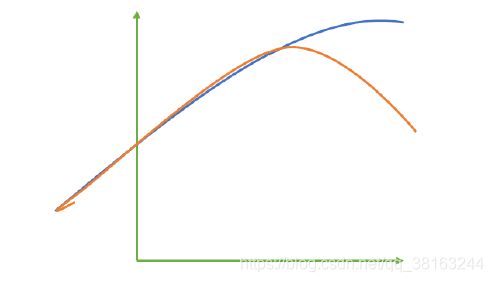
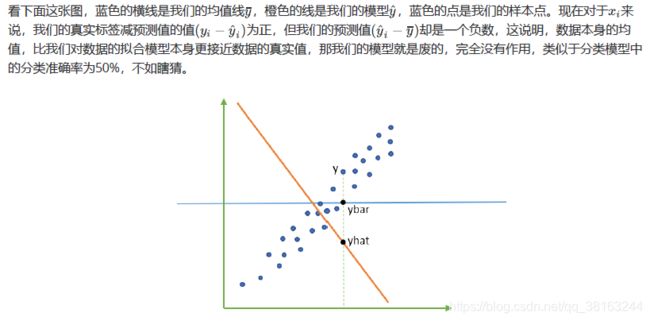
来看这张图，其中红色线是我们的真实标签，而蓝色线是我们的拟合模型。这是一种比较极端，但的确可能发生的情况。这张图像上，前半部分的拟合非常成功，看上去我们的真实标签和我们的预测结果几乎重合，但后半部分的拟合却非常糟糕，模型向着与真实标签完全相反的方向去了。对于这样的一个拟合模型，如果我们使用MSE来对它进行判断，它的MSE会很小，因为大部分样本其实都被完美拟合了，少数样本的真实值和预测值的巨大差异在被均分到每个样本上之后，MSE就会很小。但这样的拟合结果必然不是一个好结果，因为一旦我的新样本是处于拟合曲线的后半段的，我的预测结果必然会有巨大的偏差，而这不是我们希望看到的。所以，我们希望找到新的指标，除了判断预测的数值是否正确之外，还能够判断我们的模型是否拟合了足够多的，数值之外的信息。

在我们学习降维算法PCA的时候，我们提到我们使用方差来衡量数据上的信息量。如果方差越大，代表数据上的信息量越多，而这个信息量不仅包括了数值的大小，还包括了我们希望模型捕捉的那些规律。为了衡量模型对数据上的信息量的捕捉，我们定义了来帮助我们：

其中是我们的真实标签，帽是我们的预测结果，横 是我们的均值，横 如果除以样本量m就是我们的方差。方差的本质是任意一个值和样本均值的差异，差异越大，这些值所带的信息越多。在中，分子是真实值和预测值之差的差值，也就是我们的模型没有捕获到的信息总量，分母是真实标签所带的信息量，所以其衡量的是1 - 我们的模型没有捕获到的信息量占真实标签中所带的信息量的比例，所以， 越接近1越好。 可以使用三种方式来调用，一种是直接从metrics中导入r2_score，输入预测值和真实值后打分。第二种是直接从线性回归LinearRegression的接口score来进行调用。第三种是在交叉验证中，输入"r2"来调用。

 

# 调用r平方，验证模型其他的一些指标，
# 所有的回归类算法，他们的接口score默认都是r的平方
from sklearn.metrics import r2_score
r2_score(yhat,ytest)
# 这里面输入的参数是预测值和真实值
# 也就是说明捕捉到了33%比例额数据量

# 调用scoreabs接口进行预测
lr.score(xtest,ytest)
# 这里面的参数是xtest和ytest
# 在分类的评估指标中，相同的评估算法一般都有相同的评估结果，但是在回归类算法中要看清楚参数的顺序

r2_score(ytest,yhat)
# 注意参数的顺序

# 使用交叉验证进行评估
cross_val_score(lr,X,y,cv=10,scoring="r2").mean()

• 相同的评估指标不同的结果。

在我们的分类模型的评价指标当中，我们进行的是一种 if a == b的对比，这种判断和if b == a其实完全是一种概念，所以我们在进行模型评估的时候，从未踩到我们现在在的这个坑里。然而看R2的计算公式，R2明显和分类模型的指标中的accuracy或者precision不一样，R2涉及到的计算中对预测值和真实值有极大的区别，必须是预测值在分子，真实值在分母，所以我们在调用metrcis模块中的模型评估指标的时候，必须要检查清楚，指标的参数中，究竟是要求我们先输入真实值还是先输入预测值。

我们观察到，我们在加利福尼亚房屋价值数据集上的MSE其实不是一个很大的数（0.5），但我们的不高，这证明我们的模型比较好地拟合了一部分数据的数值，却没有能正确拟合数据的分布。让我们与绘图来看看，究竟是不是这样一回事。我们可以绘制一张图上的两条曲线，一条曲线是我们的真实标签Ytest，另一条曲线是我们的预测结果yhat，两条曲线的交叠越多，我们的模型拟合就越好。

# 绘制曲线查看拟合的效果
import matplotlib.pyplot as plt
plt.figure(figsize=(20,10))
plt.plot(range(len(ytest)),sorted(ytest),label="true value")
plt.plot(range(len(yhat)),sorted(yhat),label="predict value")
plt.legend()
plt.show()

可见，虽然我们的大部分数据被拟合得比较好，但是图像的开头和结尾处却又着较大的拟合误差。如果我们在图像右侧分布着更多的数据，我们的模型就会越来越偏离我们真正的标签。这种结果类似于我们前面提到的，虽然在有限的数据集上将数值预测正确了，但却没有正确拟合数据的分布，如果有更多的数据进入我们的模型，那数据标签被预测错误的可能性是非常大的。

• 负的。

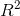除了RSS之外，我们还有解释平方和ESS（Explained Sum of Squares，也叫做SSR回归平方和）以及总离差平方和TSS（Total Sum of Squares，也叫做SST总离差平方和）。解释平方和ESS定义了我们的预测值和样本均值之间的差异，而总离差平方和定义了真实值和样本均值之间的差异（就是中的分母），两个指标分别写作：

而我们有公式：

看我们的的公式，如果带入我们的TSS和ESS，那就有：

而ESS和TSS都带平方，所以必然都是正数，那怎么可能是负的呢？因为公式TSS = RSS + ESS不是永远成立的！

 

也就是说，当我们的显示为负的时候，这证明我们的模型对我们的数据的拟合非常糟糕，模型完全不能使用。所有，一个负的是合理的。当然了，现实应用中，如果你发现你的线性回归模型出现了负的，不代表你就要接受他了，首先检查你的建模过程和数据处理过程是否正确，也许你已经伤害了数据本身，也许你的建模过程是存在bug的。如果是集成模型的回归，检查你的弱评估器的数量是否不足，随机森林，提升树这些模型在只有两三棵树的时候很容易出现负的。如果你检查了所有的代码，也确定了你的预处理没有问题，但你的也还是负的，那这就证明，线性回归模型不适合你的数据，试试看其他的算法吧。

---

参考资料：

[1] https://www.bilibili.com/video/BV1WJ411k7L3?p=228

[2] https://www.cnblogs.com/pinard/p/6004041.html

---