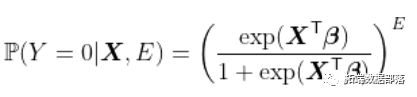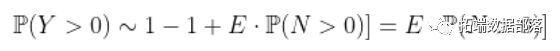r ridge回归_R语言逻辑回归和泊松回归模型对发生交通事故概率建模

原文链接 http://tecdat.cn/?p=14139

 

我们考虑风险敞口，计算包含风险敞口的多个数量(经验均值和经验方差)的非参数估计量。如果要对二项式变量建模。

这里的模型如下：

• 未观察到该期间的索赔数量 

• 索偿的数量  

考虑一种情况，其中关注变量不是索偿的数量，而仅仅是索偿发生的标志。利用泊松过程模型，我们可以获得

这意味着在一年的前六个月中没有索赔的概率是一年中没有索赔的平方根。假设可以

通过一些链接函数(使用GLM术语)表示为一些协变量来解释没有索赔的概率，

我们有

我们将使用的数据集

> T1= contrat$nocontrat[I==FALSE]> nombre2 = data.frame(nocontrat=T1,nbre=0)> sinistres = merge(contrat,nombre)> sinistres$nonsin = (sinistres$nbre==0)

我们可以考虑的第一个模型基于标准的逻辑回归方法

但是很难用标准函数处理。尽管如此，始终有可能通过数值计算给定的最大似然估计量。

> optim(fn=logL,par=c(-0.0001,-.001),+ method="BFGS")$par[1] 2.14420560 0.01040707$value[1] 7604.073$countsfunction gradient42       10$convergence[1] 0$messageNULL

现在，让我们看看基于标准回归模型的替代方案。例如对数线性模型(Logistic回归算法)。如果是指数函数(或  对数链接函数)  

现在，我们对其进行编码，

Error: no valid set of coefficients has been found: please supply starting values

尝试了所有可能的方法，但是无法解决该错误消息，

> reg=glm(nonsin~ageconducteur+offset(exposition),+ data=sinistresI,family=binomial(link="log"),+ control = glm.control(epsilon=1e-5,trace=TRUE,maxit=50),+ start=startglm,+ etastart=etaglm,mustart=muglm)Deviance = NaN Iterations - 1Error: no valid set of coefficients has been found: please supply starting values

所以我决定放弃。因为

其中接近0，

所以我们可以用泰勒展开，

在这里，暴露数不再显示为概率的幂，而是相乘。如果我们考虑对数链接函数，那么我们可以合并暴露数的对数。

最终可以完美运行了。

现在，要查看最终模型，我们回到Poisson回归模型，因为我们确实有概率模型。

现在我们可以比较这三个模型。我们还应该包括没有任何解释变量的预测。对于第二个模型，我们运行

>  regreff=glm((1-nonsin)~1+offset(log(exposition)),+ data=sinistres,family=binomial(link="log"))

预测

> exp(coefficients(regreff))(Intercept)0.06776376

可与逻辑回归比较，

> 1-exp(param)/(1+exp(param))[1] 0.06747777

但是与泊松模型有很大的不同，

(Intercept)0.07279295

我们产生一个图表比较那些模型，

> lines(age,1-yml1,type="l",col="purple")> abline(h=exp(coefficients(regreff)),lty=2)

在这里观察到这三个模型是完全不同的。实际上，使用两个模型，可以进行更复杂的回归分析(例如使用样条曲线)，以可视化年龄对发生或不发生交通事故概率的影响。如果将泊松回归(仍为红色)和对数二项式模型与泰勒展开进行比较，我们得到

点击标题查阅往期内容

R语言非参数模型厘定保险费率：局部回归、广义相加模型GAM、样条回归 R语言中自编基尼系数的CART回归决策树的实现 R语言中回归模型预测的不同类型置信区间应用比较分析 R语言中的广义线性模型(GLM)和广义相加模型(GAM)：多元(平滑)回归分析保险资金投资组合信用风险敞口 R语言中的偏最小二乘PLS回归算法 R语言对用电负荷时间序列数据进行K-medoids聚类建模和GAM回归 基于R语言的lmer混合线性回归模型 Python用PyMC3实现贝叶斯线性回归模型 r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现 R语言如何和何时使用glmnet岭回归 python用线性回归预测股票价格 偏最小二乘回归(PLSR)和主成分回归(PCR) R语言如何在生存分析与Cox回归中计算IDI，NRI指标 R使用LASSO回归预测股票收益

更多内容，请点击左下角“”查看报告全文

关注我们

案例精选、技术干货 第一时间与您分享

长按二维码加关注

更多内容，请点击左下角“”查看报告全文