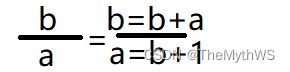【刷题宝典NO.0】
目录
素数的判定
打印素数
打印水仙花数
百钱买百坤
输出闰年
逆序打印一个整数的每一位
输出乘法口诀表
数字9出现的次数
二进制1的个数
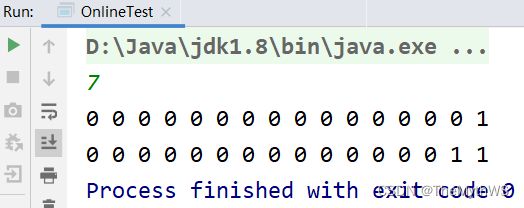
输出一个整数的偶数位和奇数位的二进制序列
求两个整数的最大公约数
求两个整数的最小公倍数
小乐乐与欧几里得
小乐乐与进制转换
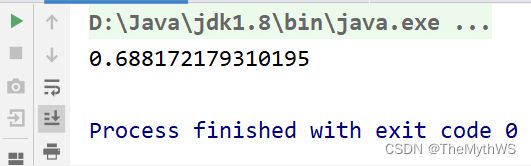
计算分数的值
计算求和
数列求和
打印各种图案
打印长方形
打印距离前面有一定空隙的长方形
打印空心正方形
打印 X 图形
打印平行四边形
打印三角形
打印菱形
打印空心菱形
小乐乐走台阶
斐波那契数列
递归实现n的k次方
递归求 N 的阶乘
递归求和
递归打印数字的每一位
返回的数字之和
素数的判定
题目内容:
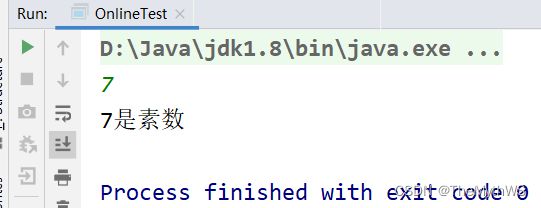
给定一个数字,判定一个数字是否是素数
import java.util.Scanner;
public class Solution {
public static void main(String[] args) {
//方法1:让n去试除2--->n-1
// Scanner sc = new Scanner(System.in);
// int n = sc.nextInt();
// int i = 2;
// for (; i <= n - 1; i++) { //让n去试除2--->n-1 比如:拿7试除2,3,4,5,6,因为7不能被2--->6内的数整除,说明7是素数
// if (n % i == 0) {
// break;
// }
// }
// if (i == n) { //如果i增长到n了,i == n > n - 1,也可以写成i > n-1 , 说明n只能被它自己整除,即素数
// System.out.println(n + "是素数");
// }
//方法2:让n去试除2--->n/2
// Scanner sc = new Scanner(System.in);
// int n = sc.nextInt();
// int i = 2;
// for (; i <= n / 2; i++) { //让n去试除2--->n/2,比如:16 :1*16 2*8 4*4 总存在一个数<=2/n
// if (n % i == 0) {
// break;
// }
// }
// if (i > n / 2) { //如果i == (2+n)/2 > n/2 了,也可以写成i > n / 2,说明n只能被它自己整除,即素数
// System.out.println(n + "是素数");
// }
//方法3:让n去试除2--->根号n
// Scanner sc = new Scanner(System.in);
// int n = sc.nextInt();
// int i = 2;
// for (; i <= Math.sqrt(n); i++) { //让n去试除2--->根号n,比如: 根号n * 根号n = n 总存在一个数<=根号n
// if (n % i == 0) {
// break;
// }
// }
// if (i > Math.sqrt(n)) { //如果i > 根号n,说明n只能被它自己整除,即素数
// System.out.println(n + "是素数");
// }
// }
//方法4:同方法3一样,多引入一个开关 在这有点多此一举
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int flag = 1; //引入一个开关,1是素数 0不是素数
int i = 2;
for (; i <= Math.sqrt(n); i++) { //让n去试除2--->根号n,比如: 根号n * 根号n = n 总存在一个数<=根号n
if (n % i == 0) {
flag = 0; //如果能被整除,说明不是素数,结束本次循环
break;
}
}
if (1 == flag) { //说明是素数
System.out.println(n + "是素数");
}
}
}打印素数
题目内容:
打印 1 - 100 之间所有的素数,并统计素数的个数
import java.util.Scanner;
public class Solution {
public static void main(String[] args) {
//方法1:引入开关
// Scanner sc = new Scanner(System.in);
// int n = sc.nextInt();
// int count = 0;
// int j = 2;
// for (; j <= n; j++) {
// int flag = 1;//引入一个开关,1是素数 0不是素数
// int i = 2;
// for (; i <= Math.sqrt(j); i++) {//让j去试除2--->根号j,比如: 根号n * 根号n = n 总存在一个数<=根号n
// if (j % i == 0) {//如果能被整除,说明不是素数,结束本次循环
// flag = 0;
// break;
// }
// }
// if (1 == flag) {//是素数就记录个数并打印
// count++;
// System.out.print(j + " ");
// }
// }
// System.out.print("count = " + count);
//方法2:改进版,将判断素数的方法封装成函数提出去
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int count = 0;
int i = 1;
for (; i <= n; i++) {
if (isPrimer(i) == 1) {
count++;
System.out.print(i + " ");
}
}
System.out.print("count = " + count);
}
//判断是否为素数
public static int isPrimer(int n) {
int i = 2;
for (; i <= Math.sqrt(n); i++) { //让n去试除2--->根号n,比如: 根号n * 根号n = n 总存在一个数<=根号n
if (n % i == 0) {
return 0;
}
}
return 1;
}
}打印水仙花数
题目内容:
求出0~100000之间的所有“水仙花数”并输出。
“水仙花数”是指一个n位数,其各位数字的n次方之和确好等于该数本身,如:153=1^3+5^3+3^3,则153是一个“水仙花数”。
public class OnlineTest {
//这是一个main方法,是程序的入口:
public static void main(String[] args) {
int i = 0;
for (i = 0; i <= 100000; i++) {
// 判断i是否为自幂数
// 1. 计算i的位数
int n = 1; // 一个数至少是一位数
int tmp = i;
while ((tmp /= 10) != 0) {
n++;
}
// 2. 得到的i的每一位,求每一位的n次方和
tmp = i;//刚刚是把tmp做了处理的,现在要重新赋值一次
int sum = 0;
while (tmp > 0) {
sum += (int) Math.pow(tmp % 10, n);
tmp /= 10;
}
if (sum == i) {
System.out.print(i + " ");
}
}
}
}百钱买百坤
public class OnlineTest {
public static void main(String[] args) {
//公鸡,母鸡,小鸡三个不是必须都有
int cock, hen, chick;
for (cock = 1; cock <= 20; cock++) {
for (hen = 1; hen <= 33; hen++) {
for (chick = 3; chick <= 99; chick += 3) {
if (cock * 5 + hen * 3 + chick / 3 == 100) {
if (cock + hen + chick == 100) {
System.out.println("公鸡:" + cock + "母鸡:" + hen + "小鸡:" + chick);
}
}
}
}
}
}
}
public class OnlineTest {
public static void main(String[] args) {
/*
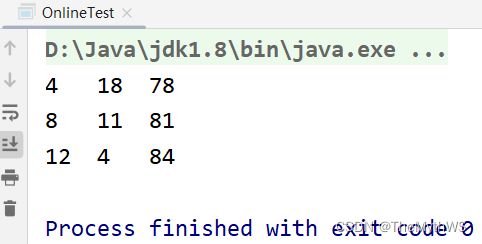
百钱买百鸡:
公鸡5文钱一只,母鸡3文钱一只,小鸡3只一文钱,
用100文钱买一百只鸡,其中公鸡,母鸡,小鸡都必须要有,问公鸡,母鸡,小鸡要买多少只刚好凑足100文钱。
数学:
设未知数:
公鸡:x只
母鸡:y只
小鸡:z只
x+y+z=100只
5x+3y+z/3=100钱
麻烦方式://下面那个代码不需要判断z%3==0,是因为每次z+=3,z的增长已经是三的倍数了。
for(int x=1;x<=100;x++){
for(int y=1;y<=100;y++){
for(int z=1;z<=100;z++){//可以修改为(int z=3;z<=100;z+=3),下面就不需要再z%3==0了。
if((x+y+z==100)&&(5*x+3*y+z/3==100)&&(z%3==0)){
System.out.println(x+"\t"+y+"\t"+z);
}
}
}
}
*/
//优化:
for (int x = 1; x <= 19; x++) {//100-1-3=96,96/5=19
for (int y = 1; y <= 31; y++) {//100-5-1=94,94/3=31
int z = 100 - x - y;
if ((5 * x + 3 * y + z / 3 == 100) && (z % 3 == 0)) {
System.out.println(x + "\t" + y + "\t" + z);
}
}
}
}
}
输出闰年
题目内容:
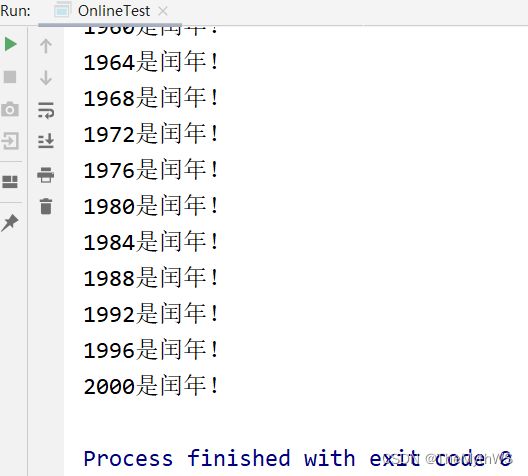
输出 1000 - 2000 之间所有的闰年
public class OnlineTest {
public static boolean isLeapYear(int year) {
// if ((year % 400 == 0) || (year % 4 == 0 && year % 100 != 0)) {
// return true;
// }else{
// return false;
// }
return ((year % 400 == 0) || (year % 4 == 0 && year % 100 != 0));
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
for (int year = 1000; year <= 2000; year++) {
boolean flag = isLeapYear(year);
if (flag == true) {
System.out.println(year + "是闰年!");
}
}
}
}逆序打印一个整数的每一位
题目内容:
逆序打印一个整数的每一位,如:123的每一位是3,2,1本题主要考虑,如何获取一个数字的每一位:
123 % 10 = 3
123/10=12 12%10=2
12/10=1 1%10= 1
import java.util.Scanner;
public class OnlineTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n != 0) {
System.out.print(n % 10 + " ");
n /= 10;
}
}
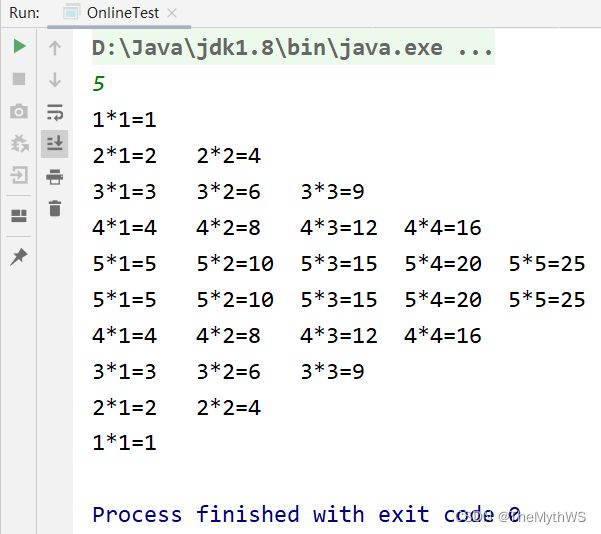
}输出乘法口诀表
题目内容:
输出n*n的乘法口诀表,n由用户输入。
import java.util.Scanner;
public class OnlineTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
System.out.print(i + "*" + j + "=" + i * j + "\t");
}
System.out.println();
}
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= i; j++) {
System.out.print(i + "*" + j + "=" + i * j + "\t");
}
System.out.println();
}
}
}数字9出现的次数
题目内容:
编写程序数一下 1到 100 的所有整数中出现多少个数字9
public class OnlineTest {
public static void main(String[] args) {
int count = 0;
for (int i = 1; i <= 100; i++) {
if (i % 10 == 9) {//判断个位的9
count++;
}
if (i / 10 == 9) {
count++;//判断十位的9
}
//多少个数字出现过9,此时99算1个数字,即一共19个
/*if (i % 10 == 9) {//判断个位的9
count++;
}
else if(i / 10 == 9) {
count++;//判断十位的9
}*/
}
System.out.println(count);
}
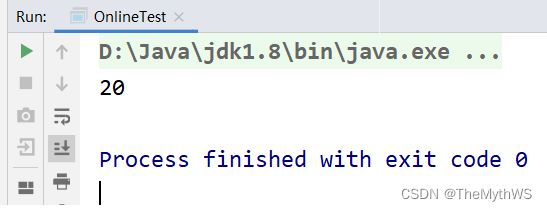
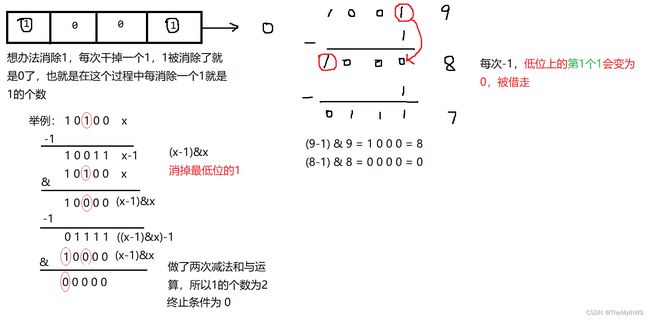
}二进制1的个数
题目内容:
求一个整数,在内存当中存储时,二进制1的个数。
import java.util.Scanner;
public class OnlineTest {
//方法1:
/*public static int numberOf1(int n) {
int count = 0;
for (int i = 0; i < 32; i++) { //n可以在2进制中表示32位,每次让n无符号向右移动一位,每一位和1相与
if (((n >>> i) & 1) == 1) {
count++;
}
}
return count;
}*/
//方法2:
/*public static int numberOf1(int n) {
int count = 0;
*//*for (int i = 0; i < 32; i++) {
if ((n & 1) == 1) {
count++;
}
n >>>= 1;
}*//*
while (n != 0) {
if ((n & 1) != 0) {
count++;
}
n >>>= 1;
}
return count;
}*/
//方法3:n & (n - 1) 每次消去一个1,记录消去1的次数,直到1全部被消去变为0为止
public static int numberOf1(int n) {
int count = 0;
while (n != 0) {
n = n & (n - 1); //n &= n - 1;
count++;
}
return count;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int ret = numberOf1(n);
System.out.println(ret);
}
}输出一个整数的偶数位和奇数位的二进制序列
import java.util.Scanner;
public class OnlineTest {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
//偶数位 下标从1开始(第二个数),每次让n右移2位让偶数位 和 1做 & 运算,如果结果是1说明当前偶数位是1,同理结果是0。。。
for (int i = 31; i >= 1 ; i-=2) {
System.out.print(((n >> i) & 1)+" ");
}
System.out.println();
//奇数位 下标从0开始(第一个数),每次让n右移2位让奇数位 和 1做 & 运算,如果结果是1说明当前奇数位是1,同理结果是0。。。
for (int i = 30; i >= 0 ; i-=2) {
System.out.print(((n >> i) & 1)+" ");
}
}
}求两个整数的最大公约数
题目内容:
给定两个数,求这两个数的最大公约数例如:
输入:20 40
输出:20
import java.util.Scanner;
public class OnlineTest {
public static void main(String[] args) {
//方法1:找出m和n之间的最小值min,用m和n同时对min整除,如果同时被整除,那么这个min就是最大公约数,如果不能整除,那么就min--
/*Scanner in = new Scanner(System.in);
int m = in.nextInt();
int n = in.nextInt();
int min = m > n ? n : m;
while (true) {
if (m % min == 0 && n % min == 0) {
System.out.println("最大公约数:" + min);
break;
}
min--;
}*/
//方法2:辗转相除法 m % n = r ,如果r != 0,m = n,n = r,当r = 0时,n为最大公约数
// 例如:m:24 n:18 第一次:m % n = 24 % 18 = 6 第二次:18 % 6 = 0,6为最大公约数
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int n = in.nextInt();
/*int r = m % n;
while (r != 0) {
m = n;
n = r;
r = m % n;
}*/
int r = 0;
while ((r = m % n) != 0) {
m = n;
n = r;
}
System.out.println("最大公约数:" + n);
}
}求两个整数的最小公倍数
题目内容:
给定两个数,求这两个数的最小公倍数例如:
输入:12 15
输出:60
import java.util.Scanner;
public class OnlineTest {
public static void main(String[] args) {
//找出m和n之间的最大值max,用max对m和n整除,如果同时整除了m和n,那么这个max就是最小公倍数,如果不能整除,那么就max++
Scanner in = new Scanner(System.in);
int m = in.nextInt();
int n = in.nextInt();
int max = m > n ? m : n;//或者int max = Math.max(m, n);
while (true) {
if (max % m == 0 && max % n == 0) {
System.out.println("最小公倍数:" + max);
break;
}
max++;
}
}
}小乐乐与欧几里得
https://www.nowcoder.com/share/jump/4389976241698855052246
描述
小乐乐最近在课上学习了如何求两个正整数的最大公约数与最小公倍数,但是他竟然不会求两个正整数的最大公约数与最小公倍数之和,请你帮助他解决这个问题。
输入描述:
每组输入包含两个正整数n和m。(1 ≤ n ≤ 109,1 ≤ m ≤ 109)
输出描述:
对于每组输入,输出一个正整数,为n和m的最大公约数与最小公倍数之和。
示例1
输入:
10 20
输出:
30
示例2
输入:
15 20
输出:
65
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
long m = scanner.nextLong();
long n = scanner.nextLong();
long m2 = m;
long n2 = n;
long r = 0;
//最大公约数
while ((r = m2 % n2) != 0) {
m2 = n2;
n2 = r;
}
long max = n2;
//最小公倍数:m * n / 最大公约数
long min = m * n / n2;
System.out.println(max + min);
}
}
小乐乐与进制转换
https://www.nowcoder.com/share/jump/4389976241698856221648
描述
小乐乐在课上学习了二进制八进制与十六进制后,对进制转换产生了浓厚的兴趣。因为他的幸运数字是6,所以他想知道一个数表示为六进制后的结果。请你帮助他解决这个问题。
输入描述:
输入一个正整数n (1 ≤ n ≤ 109)
输出描述:
输出一行,为正整数n表示为六进制的结果
示例1
输入:
6
输出:
10
示例2
输入:
120
输出:
320
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int arr[] = new int[20];
int i = 0;
while (n > 0) {
arr[i] = n % 6;
n /= 6;
i++;
}
for (--i; i >= 0; i--) {
System.out.print(arr[i]);
}
}
}
计算分数的值
题目内容:
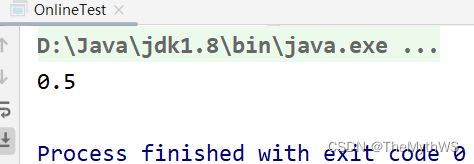
计算1/1-1/2+1/3-1/4+1/5 …… + 1/99 - 1/100 的值 。思路:
1. 从上述表达式可以分析出
该表达式主要由100项,奇数项为正,偶数项为负
2. 设置一个循环从1~100,给出表达式中的每一项:1.0/i, 注意此处不能使用1,否则结果全部为0
然后使用flag标记控制奇偶项,奇数项为正,偶数项为负
然后将所有的项相加即可
public class OnlineTest {
//这是一个main方法,是程序的入口:
public static void main(String[] args) {
double sum = 0.0;
int flag = 1;
for (int i = 1; i <= 100; i++) {
sum += 1.0 * flag / i;
flag = -flag;
}
System.out.println(sum);
}
}计算求和
题目内容:
求Sn=a+aa+aaa+aaaa+aaaaa的前5项之和,其中a是一个数字,
例如:2+22+222+2222+22222
import java.util.Scanner;
public class OnlineTest {
//这是一个main方法,是程序的入口:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int a = scanner.nextInt();
int n = scanner.nextInt();
int i = 0;
int Sn = 0;
int k = 0;
for (i = 0; i < n; i++) {
k = k * 10 + a;
Sn += k;
}
System.out.println(Sn);
}
}数列求和
数列求和
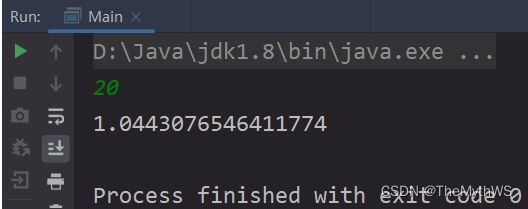
前n(n<=20)项之和。(不使用if…else等选择分支语句)
思路:
1.推导公式:2.每次循环累加的时候符号要变换,引入一个开关,控制正负号
3.在循环里面的时候a的值每次还要减a,不然a会一直累加,a的值是相对于上个式子的b基础上+1的
import java.util.Scanner;
public class Main {
//这是一个main方法,是程序的入口:
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
//b/a == b=a+b/a=b+1
double b = 2; //起始分子
double a = 1; //起始分母
double sum = 0.0;
int flag = 1;
for (int i = 0; i < n; i++) {
sum += 1.0 * flag * b / a; //累加
b += a; //分子
a = b + 1 - a; //分母 注意这儿每次循环要-a,因为每次循环分母a的值会累加,a的值是相对于上个式子的b基础上+1
flag = -flag;
}
System.out.println(sum);
}
}打印各种图案
打印长方形
public class OnlineTest {
public static void main(String[] args) {
for (int j = 1; j <= 4; j++) {//j:控制行数
//*********
for (int i = 1; i <= 9; i++) {//i:控制*的个数
System.out.print("*");
}
//换行:
System.out.println();
}
}
}
打印距离前面有一定空隙的长方形
public class OnlineTest {
public static void main(String[] args) {
for (int j = 1; j <= 4; j++) {//j:控制行数
//加入空格:
for (int i = 1; i <= 5; i++) {//i:控制空格的个数
System.out.print(" ");
}
//*********
for (int i = 1; i <= 9; i++) {//i:控制*的个数
System.out.print("*");
}
//换行:
System.out.println();
}
}
}
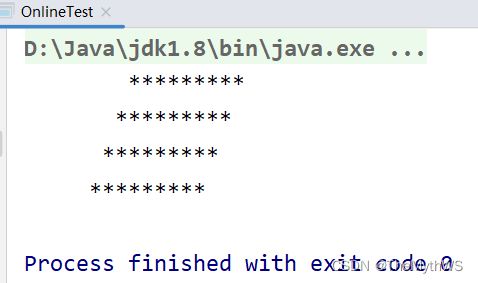
打印空心正方形
https://www.nowcoder.com/share/jump/1698854024034
描述
KiKi学习了循环,BoBo老师给他出了一系列打印图案的练习,该任务是打印用“*”组成的“空心”正方形图案。
输入描述:
多组输入,一个整数(3~20),表示输出的行数,也表示组成正方形边的“*”的数量。
输出描述:
针对每行输入,输出用“*”组成的“空心”正方形,每个“*”后面有一个空格。
示例1
输入:
4输出:
* * * * * * * * * * * *示例2
输入:
5输出:
* * * * * * * * * * * * * * * *
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ((i == 0) || (i == n - 1) || (j == 0) || (j == n - 1))
System.out.print("* ");
else
System.out.print(" ");
}
System.out.println();
}
}
scanner.close();
}
}
打印 X 图形
https://www.nowcoder.com/practice/83d6afe3018e44539c51265165806ee4
描述
KiKi学习了循环,BoBo老师给他出了一系列打印图案的练习,该任务是打印用“*”组成的X形图案。
输入描述:
多组输入,一个整数(2~20),表示输出的行数,也表示组成“X”的反斜线和正斜线的长度。
输出描述:
针对每行输入,输出用“*”组成的X形图案。
示例1
输入:
5
复制输出:
* *
* *
*
* *
* *复制
示例2
输入:
6
复制输出:
* *
* *
* *
* *
* *
* *
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextInt()) { // 注意 while 处理多个 case
int n = in.nextInt();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if ((i == j) || (i + j == n - 1)) {
System.out.print("*");
} else {
System.out.print(" ");
}
}
System.out.println();
}
}
}
}打印平行四边形
public class OnlineTest {
public static void main(String[] args) {
for (int j = 1; j <= 4; j++) {//j:控制行数
//加入空格:
for (int i = 1; i <= (9 - j); i++) {//i:控制空格的个数
System.out.print(" ");
}
//*********
for (int i = 1; i <= 9; i++) {//i:控制*的个数
System.out.print("*");
}
//换行:
System.out.println();
}
}
}
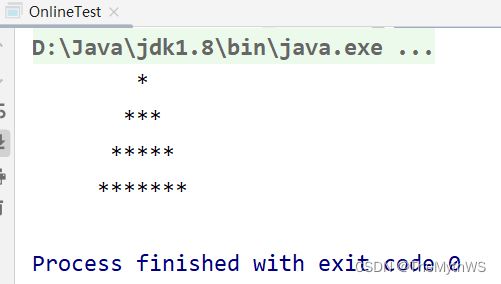
打印三角形
public class OnlineTest {
public static void main(String[] args) {
for (int j = 1; j <= 4; j++) {//j:控制行数
//加入空格:
for (int i = 1; i <= (9 - j); i++) {//i:控制空格的个数
System.out.print(" ");
}
//*********
for (int i = 1; i <= (2 * j - 1); i++) {//i:控制*的个数
System.out.print("*");
}
//换行:
System.out.println();
}
}
}
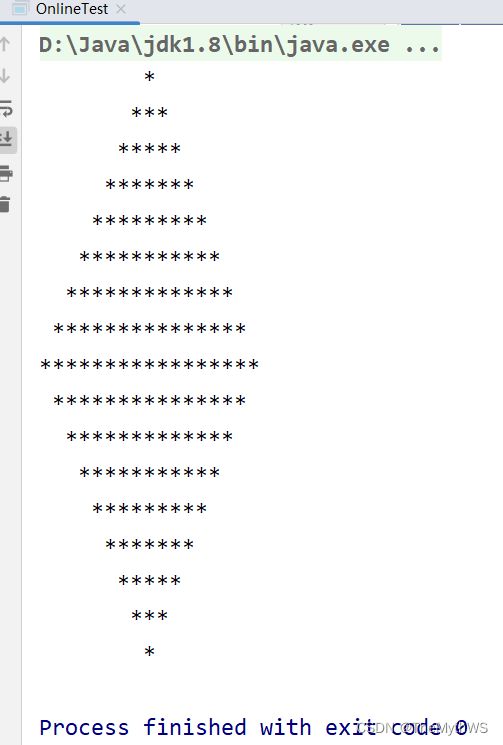
打印菱形
public class OnlineTest {
public static void main(String[] args) {
//上面三角形:
for (int j = 1; j <= 4; j++) {//j:控制行数
//加入空格:
for (int i = 1; i <= (9 - j); i++) {//i:控制空格的个数
System.out.print(" ");
}
//*********
for (int i = 1; i <= (2 * j - 1); i++) {//i:控制*的个数
System.out.print("*");
}
//换行:
System.out.println();
}
//下面三角形:
for (int j = 1; j <= 3; j++) {//j:控制行数
//加入空格:
for (int i = 1; i <= (j + 5); i++) {//i:控制空格的个数
System.out.print(" ");
}
//*********
for (int i = 1; i <= (7 - 2 * j); i++) {//i:控制*的个数
System.out.print("*");
}
//换行:
System.out.println();
}
}
}
public class OnlineTest {
public static void main(String[] args) {
//先打印出一个正方形,然后某些位置上打印* 某些位置上打印空格:
int size = 17;
int startNum = size / 2 + 1;//起始列号
int endNum = size / 2 + 1;//结束列号
//引入一个布尔类型的变量---》理解为“开关”
boolean flag = true;
for (int j = 1; j <= size; j++) {
//*****
for (int i = 1; i <= size; i++) {
if (i >= startNum && i <= endNum) {
System.out.print("*");
} else {
System.out.print(" ");
}
}
//换行
System.out.println();
if (endNum == size) {
flag = false;
}
if (flag) {//flag是true相当于在菱形的上半侧 flag是false相当于在菱形的下半侧
startNum--;
endNum++;
} else {
startNum++;
endNum--;
}
}
}
}
打印空心菱形
public class OnlineTest {
public static void main(String[] args) {
//先打印出一个正方形,然后某些位置上打印* 某些位置上打印空格:
int size = 17;
int startNum = size / 2 + 1;//起始列号
int endNum = size / 2 + 1;//结束列号
//引入一个布尔类型的变量---》理解为“开关”
boolean flag = true;
for (int j = 1; j <= size; j++) {
//*****
for (int i = 1; i <= size; i++) {
if (i == startNum || i == endNum) {
System.out.print("*");
} else {
System.out.print(" ");
}
}
//换行
System.out.println();
if (endNum == size) {
flag = false;
}
if (flag) {//flag是true相当于在菱形的上半侧 flag是false相当于在菱形的下半侧
startNum--;
endNum++;
} else {
startNum++;
endNum--;
}
}
}
}
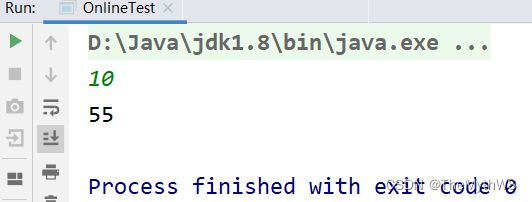
小乐乐走台阶
https://www.nowcoder.com/share/jump/4389976241698854945904
描述
小乐乐上课需要走n阶台阶,因为他腿比较长,所以每次可以选择走一阶或者走两阶,那么他一共有多少种走法?
输入描述:
输入包含一个整数n (1 ≤ n ≤ 30)
输出描述:
输出一个整数,即小乐乐可以走的方法数。
示例1
输入:
2
输出:
2
示例2
输入:
10
输出:
89
import java.util.Scanner;
public class Main {
public static int walk(int n) {
if (n <= 2) {
return n;
} else {
return walk(n - 1) + walk(n - 2);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int ret = walk(n);
System.out.println(ret);
scanner.close();
}
}
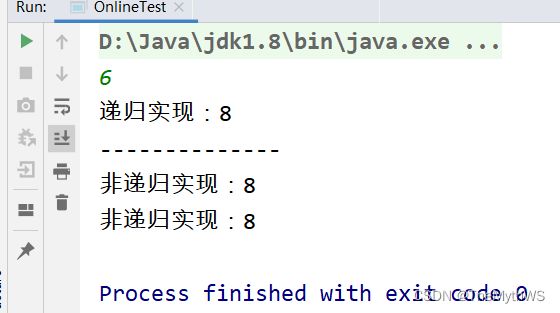
斐波那契数列
题目内容:
求斐波那契数列的第n项。(迭代实现)
斐波那契数列定义为:1 1 2 3 5 8 13 21 我们可以看到,从第3项开始,都等于前一项+前一项的前一项的和。
3=1+2
5+2+3
13 = 5+8
我们可以先定义f1保存第一项的值,f2保存第2项的值,f3保存第3项的值。
每次算法一个f3,就同步更新f1和f2的值。
import java.util.Scanner;
public class OnlineTest {//1.递归实现斐波那契数列
public static int fib1(int n) {
if (n <= 2) {
return 1;
} else {
return fib1(n - 1) + fib1(n - 2);
}
}
//2. fib: 1 1 2 3 5
// a + b = c
// a + b = c
// n: 1 2 3 4 5
// n = 3,即n > 2时,有 c = a + b ; a = b ; b = c
public static int fib2(int n) {
int a = 1;
int b = 1;
int c = 0;
while (n > 2) {//从第三项开始
c = a + b;
a = b;
b = c;
n--;
}
return c;
}
public static int fib3(int n) {
if (n == 1 || n == 2) {
return 1;
}
int f1 = 1;
int f2 = 1;
int f3 = 0;
for (int i = 3; i <= n; i++) {
f3 = f1 + f2;
f1 = f2;
f2 = f3;
}
return f3;
}
//这是一个main方法,是程序的入口:
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int ret1 = fib1(n);
int ret2 = fib2(n);
int ret3 = fib3(n);
System.out.println("递归实现:" + ret1);
System.out.println("--------------");
System.out.println("非递归实现:" + ret2);
System.out.println("非递归实现:" + ret3);
}
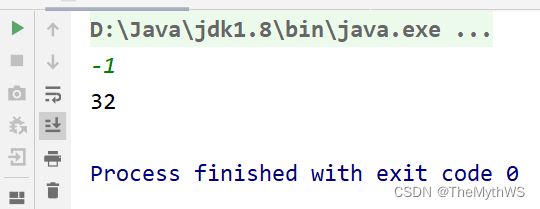
}递归实现n的k次方
public class OnlineTest {
public static void main(String[] args) {
int n = 2;
int k = -1;
System.out.println(power(n, k));
}
public static double power(int n, int k) {
if (k == 0) {
return 1;
} else if (k > 0 ){
return n * power(n, k - 1);
} else {//k < 0
return 1.0 / power(n, -k);
}
}
}
递归求 N 的阶乘
题目内容:
递归求 N 的阶乘
递归代码重要的是推导递推公式:假设N的阶乘用F(n)表示,那么F(n) = n * F(n-1);
import java.util.Scanner;
public class OnlineTest {
public static int fac(int n) {
if(n < 2) {
return 1;
}
return n * fac(n-1);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(fac(n));
}
}递归求和
题目内容:
递归求 1 + 2 + 3 + ... + 10假设用F(n) 代表1-n的和,那么F(n) = n + F(n-1)的和
F(n-1)就是1到n-1的和
import java.util.Scanner;
public class OnlineTest {
public static int sum(int n) {
if(n == 1) {
return 1;
}
return n + sum(n-1);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(sum(n));
}
}递归打印数字的每一位
题目内容:
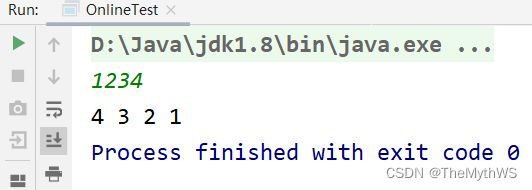
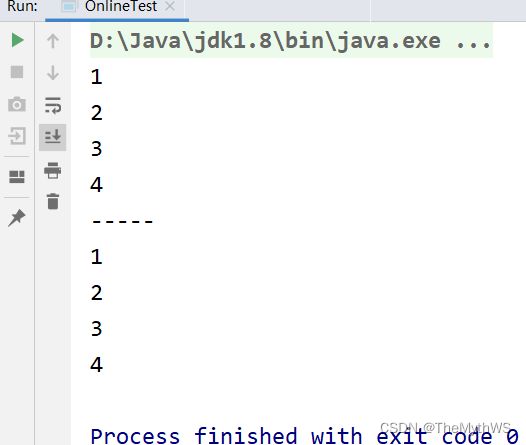
按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4) (递归)
假设用F(n) 代表 要顺序打印n的每一位,如果n是一个1位数,直接输出,如果n是2位数以上。
如:
123 相当于先打印12的每一位,再打印3
12 相当于先打印1的每一位,再打印2
1 只有一位数,直接打印。
依次回退打印完,每一位即可。
public class OnlineTest {
//写法1:
public static void print(int num) {
if (num > 9) {
print(num / 10);
}
System.out.println(num % 10);
}
//写法2:
public static void fun(int n) {
if (n <= 9) {
System.out.println(n);
return; //出口,不然会栈溢出错误(必须由程序员解决)
}
fun(n / 10);
System.out.println(n % 10);
}
public static void main(String[] args) {
fun(1234);
System.out.println("-----");
print(1234);
}
}返回的数字之和
题目内容:
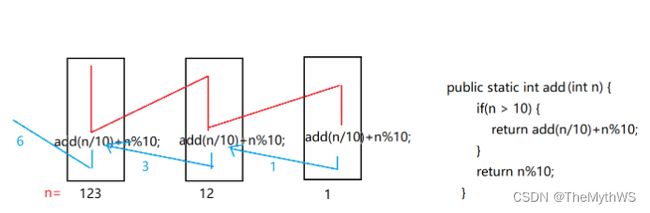
写一个递归方法,输入一个非负整数,返回组成它的数字之和要计算123的每一位,主要在于如何得到每一位。在前面的习题中我们知道,除10 , 模10.可以做到。
如下图,在执行n=123的时候,先执行add(123/10)也就是add(12)这个函数,等最后回来之后,才会把n=123时候的n%10算完。
public class OnlineTest {
public static int digitSum(int n) {
if (n <= 9) {
return n;
}
return n % 10 + digitSum(n / 10);
}
public static void main(String[] args) {
System.out.println(digitSum(1729));
}
}