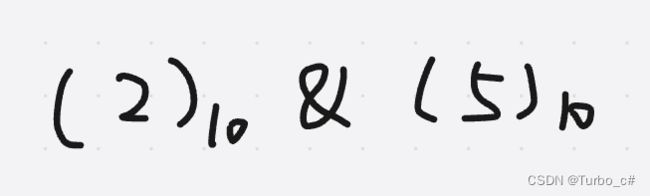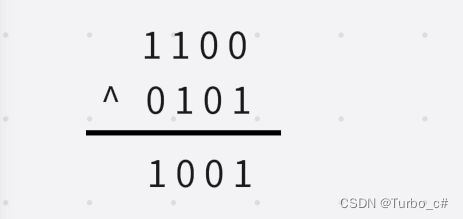与或异或位运算(只出现一次的数字)
与&运算
与运算就是当两个二进制进行对比时,如果都是1就是1,只要遇到0就是0。
如下2和5进行与运算
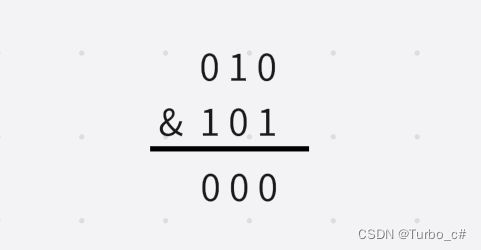
那么2的二进制就是10,5的二进制就是101
遇到0便是0,两个都是1的时候就是1
或|运算
或运算就是遇到1便是1,如下:
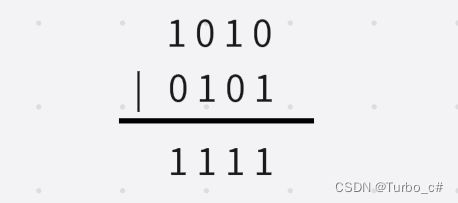
10的二进制是1010,5的二进制是0101,上下一对比都是就是1111
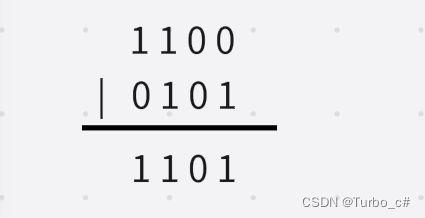
12 | 5的时候,上下都是0,所以为0。
异或运算^
异或运算是一样的时候为0,不一样为1
左移<<运算
规则:
右边空出的位用0填补
高位左移溢出则舍弃该高位。
示例:
该图的意思就是二进制101左移一位,那么二进制101就是十进制的5。
左移一位就是右边补零。该图就是左移一位的结果,十进制是10。这么聪明的你,很快就能发现规律没错,左移一位十进制就乘2。原理就是你原有的二进制位向左移了一位,相当于乘2,所以十进制数也是乘2.
右移>>运算
规则:
左边空出的位用0或者1填补。正数用0填补,负数用1填补。
低位右移溢出则舍弃该位。
示例:
该图就是二进制10101右移1位
右移一位后就变成二进制1010,同理,右移一位十进制除2,向下取整。(因为最后一个1右移后就没了)
那么,有人就会开始疑问了?这些能做些什么呢?
像leetcode的算法题里面就有
运用位运算的算法题
只出现过一次的数字
题目解释:在数组里面有若干个数字,但是有一个数字只出现一次,其余数字都是出现两次
方法一:使用哈希表或者集合
使用哈希表,建立一个哈希表,存放每个数字的次数,然后循环找到出现为1的次数。
但是题目写明不能使用额外的空间,所以方法一pass。
方法二:使用位运算
对于这道题,可使用异或运算 。异或运算有以下三个性质。
任何数和 000 做异或运算,结果仍然是原来的数,即 a^0=a
任何数和其自身做异或运算,结果是 000,即 a^a=0
异或运算满足交换律和结合律,即 a^b^a=b^a^a=b^(a^a)=b^0=b
所以套用这个异或的关系可以产生一旦有两个数字是相同的便可以直接等于0;
题目写明了,只有一个数字就是只出现一次,其余数字都是出现两次,所以所有数进行异或运算,最后只会留下单独的数字。
int singleNumber(vector& nums) {
int ans = 0;
for(auto &num : nums) //能够循环遍历nums数组中的数字
{
ans ^= num; //将每次循环的数字进行异或运算
}
return ans;
} 复杂度分析
-
时间复杂度:O(n),其中 n是数组长度。只需要对数组遍历一次。
-
空间复杂度:O(1)。
环和杆
今天的leetcode每日一题就是这个,属于简单题可以使用哈希表也可以使用位运算
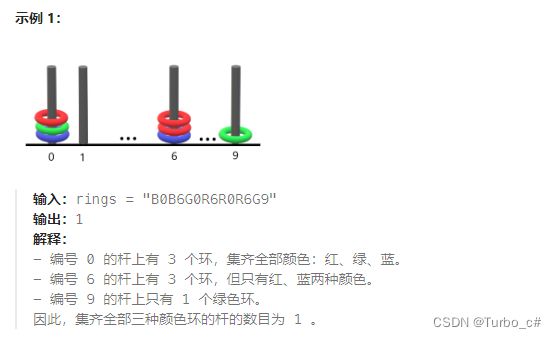
简单的解释一下这个题目的意思,就是说有十个杆子,每个杆子能存放不同颜色的圆环,当一个杆子有红 = ‘R’ ,蓝 = ' B' , 绿 = ‘G’ 三种颜色的圆环则累计一次,如图所示。
位运算
在使用位运算做这题之前,我们先复习一下<<左移运算符,能够将二进制左移n位。
那么利用这个特性,我们可以将26个字母左移多次,比如说A就是移动0次,那么在二进制中表示1,B是移动1次,左移一次就是10,以此类推。每个字母都有相对应的二进制来表示。
|运算呢,就是遇到1就是1,那么我们可以利用这个特性,例如,原来的mark是0
那么mark = 0 | 100 (C)就是 100,接着 mark = 100 | 010(B), mark最后的答案就是110,也就是BC。
那么我们就可以提前把R G B的二进制存放到一个变量mark中
int mark = 0;
mark |= 1 << 'R' - 'A'; // 移动ASCII确定左移的次数,比如说‘R’在ASCII码中是 82 减去'A'的65,就是17,那么就是1的二进制左移17次。
mark |= 1 << 'G' - 'A'; //|=在这里的作用就是每次,都能够把二进制存放到mark当中。
mark |= 1 << 'B' - 'A';接着就是整体思路我们可以用一个长度为 10 的数组 deposit 来表示每根杆上的环的颜色情况,其中 deposit [i]表示第 i 根杆上的环的颜色情况,如果第 i根杆上有红色、绿色、蓝色的环那么它的二进制就会和mark一样。
我们遍历字符串 rings,rings[i+1]表示环所在的杆的编号,rings[i]表示该环的颜色。我们将该环放进deposit数组中。
最后我们统计 deposit 中值和mark元素相同的个数,即为集齐全部三种颜色环的杆的数目。
最后代码如下:
int countPoints(string rings) {
vector deposit(10);
int mark = 0;
mark |= 1 << 'R' - 'A';
mark |= 1 << 'G' - 'A';
mark |= 1 << 'B' - 'A';
for(int i = 0;i 复杂度分析
-
时间复杂度:O(n),其中 n是数组长度。
-
空间复杂度:O(m)。m 表示字符集的大小