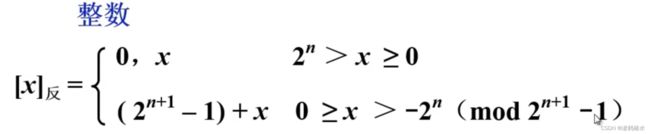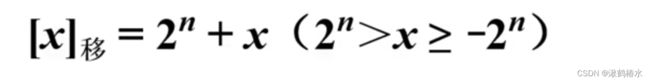计算机组成原理(三)
C、中断设备向量地址形成部件
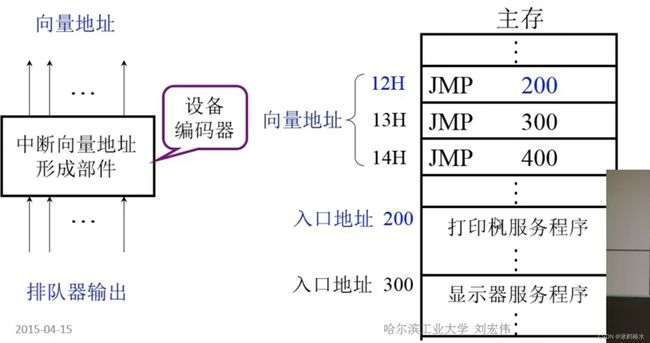
- 在排队器处理完毕之后,所有的INTER线(仅有一条是低电平)经过设备向量地址形成部件后,设备向量地址形成部件给出中断响应程序首地址,CPU在收到中断指令后,根据提供的中断程序首地址从主存中取出指令,进行执行,下图是主存和向量地址在主存中的位置:
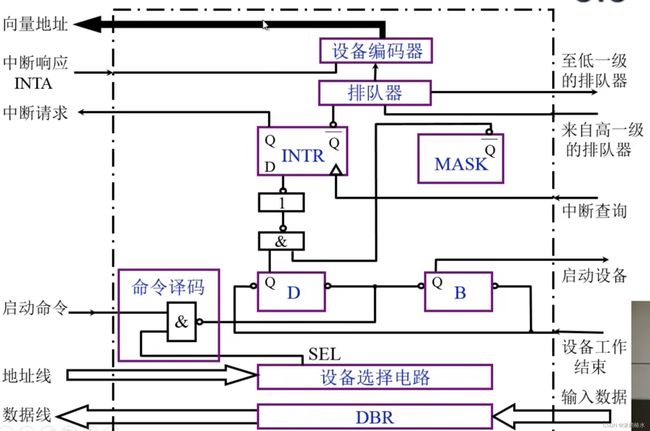
D、综上我们可以给出一个中断响应方式I/O的接口较完整的结构
地址线经过设备选择电路发出设备选择信号----> 启动命令经过命令译码器后令D(完成触发器)为0,B(状态触发器)为1----> B向设备发出启动命令,设备开始启动 --->设备工作结束返回数据到DBR,同时改变B和D为0和1---> D为1后,和MASK(屏蔽触发器)一起经过与非门和非门,将电流输送到INTR----> 多个INTR(同时工作)经过排队器排队后,输送到设备编码器--->设备编码器,给出中断程序首地址---> CPU收到中断指令之后开始执行中断程序。
(四)I/O 中断处理过程
A、EINT(允许中断触发器)
默认EINT为0,不允许执行中断程序,当CPU查询到有中断指令且优先级高于现执行程序,则将EINT调为1,开始执行中断程序,执行完毕后调用指令恢复,或者物理硬件反弹。
B、中断执行的时间点
在一条指令执行阶段结束前,CPU会检测是否有中断指令,如果有就开始执行中断程序
十三、中断服务程序的流程
(一)流程概览
A、执行保护程序,在中断之前,保存程序执行断点(依靠隐指令执行,隐指令就是硬件自动调用,程序无法调用),同时将程序需要用到的寄存器中的值保存起来,等待中断程序执行完毕之后,原程序恢复执行
这里保存原程序数据的方法有很多种,包括使用入栈指令将数据压入保护程序、或者将数据保存到其他暂时空闲的寄存器,或者保存到主存之中。
B、中断服务,执行中断服务指令(不同I/O接口会有不同的中断服务)
C、执行中断服务完毕后,执行出栈指令,恢复原程序数据。
D、执行中断返回指令,继续执行原程序
(二)单重中断和多重中断
A、单重中断:当有中断程序正在执行时,如果有优先级更高的中断请求,仍然执行本中断程序。
B、多重中断:当有中断程序正在执行时,如果有优先级更高的中断请求,允许程序被中断后执行新的中断程序。
C、两重中断的区别:
- 在红框框起来的位置我们看到单重中断是在设备服务完成后,才打开中断允许(开中断),然后中断返回,而多重中断是在进入中断服务后,保护完现场(将寄存器中需要的数据存入其他位置)直接打开中断允许,允许其他中断请求继续中断。
(三)总揽优劣
宏观上看,I/O接口和CPU是并行工作的,主要体现在(I/O接口在启动外部设备时,CPU仍然在运行主程序)
从微观上看,当外部设备准备完成后,还是要通过中断指令占用CPU,主进程还是要被搁置,故又是串行化的,还显劣势。
十四、DMA方式(直接存储器访问)
(一)DMA方式和程序中断、查询方式的数据通路的不同
DMA方式将CPU从外部设备和主存的数据交换中解脱出来。从前面我们可以知道,程序查询方式和程序中断方式都必须要用CPU一个寄存器作为媒介,传递数据,这样CPU就参与到外部设备和主存的数据交换中,严重浪费CPU的性能。
- 从图中可以看出DMA方式可以直接将外部设备和主存构成通路,实现内外数据的直接传递,解放了CPU这一宝贵资源。
(二)DMA与主存交换数据的三种方式
A、方式一:直接占用主存和总线使用权
这种方式虽然简单,但是有很大弊端。当DMA占用主存后,CPU因为失去主存占有权,就处于不工作状态或保持状态(指令缓冲区中有指令但无法从主存中获取想要的数据),DMA占用主存后,因为数据的传输不是一次传输完成的,而是要一次一次传输,所以中间有很长时间,DMA方式是对主存的占用是处于空闲状态的,这严重浪费了CPU的性能。
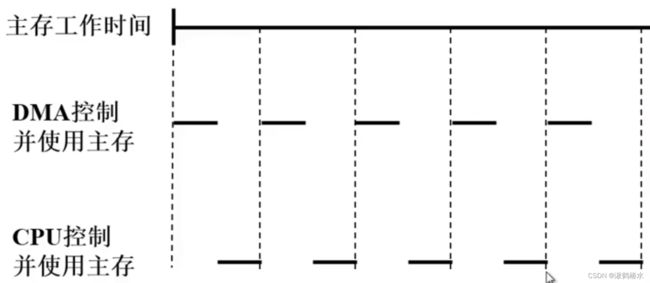
B、方式二:周期窃取(周期挪用)
这种方式是DMA在数据准备好后,发出总线占用请求,占用总线一个访存周期,数据传输完毕后,放弃总线使用权,还给CPU,这样就充分利用了总线和主存,减少了主存对CPU性能的消耗。
在DMA发出总线占用请求时会出现三种情况:1、总线闲置,直接占用 2、CPU正在占用主线,要等待CPU数据访存完毕。 3、CPU和DMA同时申请占用,则CPU要让出主线占用权(因为DMA通常连接的都是高速外部设备,如果等待时间过长,容易造成数据丢失。)
下面是这种方式的时间对比图:
C、DMA与CPU交替访问
我们将DMA和CPU分成等分的工作周期,DMA和CPU交替占用工作周期进行工作。这样做避免了DMA和CPU频繁交换总线和主存的占用权(提出占用申请和返回同意申请也是需要时间的),这样也就节省了一些时间(这样不需要申请占用和归还主线及主存的使用权)
(三)DMA接口的组成
A、DMA接口要实现的功能
- 向CPU申请DMA传送。
- 处理总线 控制权转交工作
- 管理系统总线、控制数据传送
- 确定数据传送的首地址和长度,修正传送过程中数据的地址和长度。
- 当DMA传送结束时,给出操作完成信号。
B、DMA的组成
分析:
- 三个组件AR(传送首地址寄存器)、WC(是字节数,会存一次不能传完全部数据,该寄存器用来记录已经传完的数据)、DAR(外部设备编号寄存器,用来确认是否是该DMA对应的外部设备)
- BR(数据缓冲,用来咱存数据)、中断机构是在数据传送完毕(WC归零)时,中断机构在数据缓冲完毕后发出中断请求,结束数据传送。
- DMA逻辑控制单元,用来控制整个DMA电路的调换,同时负责发出设备启动请求和设备启动反馈等。
分析数据输入过程
设备将数据存入BR---> 然后向控制逻辑单元发出请求信号---> 控制单元收到请求信号后,发出总线占用请求--->如果CPU未占用,则获得总线控制权 (CPU给出总线允许信号HLDA)---->AR接入总线中的地址线生效,存入位置被选中---->控制单元返回DMA正在传输数据的信号给外部设备--->控制单元控制数据线将BR中数据根据AR提供的地址,存入主存当中--->储存完毕后增加WC(字计数器)的值,改变AR(使指向下一个地址)--->最后检查WC,中断机构根据自身中断触发器判断是否发出停止DMA服务的请求信号(中断请求)。
C、CPU参与下的DMA数据传送过程
CPU预处理阶段,其会将DMA所需要的连接的设备码(DAR)发送到DMA的DAR寄存器、将主存首地址(AR)发送到DMA寄存器、将WC发送到WC寄存器中;上面用作DMA的初始化前提;
DMA数据传送阶段:首先发出总线占用请求,判断是否可占用--->如果可占用,首先将自身AR保存的主存地址发到总线--->然后将数据送I/O设备(或主存)--->单次数据传送完毕后,修改AR指向下一个要保存(或取出)的内存单元,修改字计数器 --->最后检查字计数器看数据是否全部传输完成--->如果没有就再次进行传送数据流程,如果已经结束,就向CPU申请程序中断
后处理阶段:CPU收到DMA程序中断指令之后,执行中断服务程序,结束DMA的工作状态。
- 后处理是在DMA发出程序中断指令后,CPU执行中断服务程序时要进行的过程,包括三个方面:
- 验证存入主存中数据的准确性
- 检查是否还需要DMA服务
- 验证数据存入或取出过程是否出现错误
(四)DMA接口与系统的连接细节
A、具有公共请求线的DMA请求
多个DMA接口共享一条DMA请求线连接到CPU,当CPU收到DMA请求时,会按DMA响应电路依次查看接口是否发出DMA请求,先查询到的接口获得总线访问权限。(离CPU越近的DMA接口越占优势。
B、具有独立请求线的DMA请求
这种方式每个接口都有一个独立的请求线,这样CPU在收到请求后,根据自己的算法或优先级设置给出主存和总线控制权限(通过响应线来响应) ,这种方式更加灵活。
(五)程序中断方式和DMA方式的对比
| 程序中断方式 | DMA方式 | |
| 数据传送 | 程序(CPU调用指令来传送) | 硬件(由DMA中控制单元控制传送) |
| 响应时间 | 一个指令执行完毕 | 一个存储周期(CPU一个存储周期后即可获得主存和总线的控制权) |
| 处理异常情况 | 能(中断程序出错后亦可以被中断) | 不能(数据传输过程,由硬件控制,没有中断机制) |
| 中断请求目的 | 为了执行中断程序传递数据 | 为了执行中断程序,进行数据传递完毕后的后处理工作 |
| 优先级 | 低(中断方式一般连接低速设备) | 高(DMA方式,一般连接高速外部设备) |
(六)DMA接口的分类
A、选择型(多个外部设备对接一个DMA接口)
当CPU需要外部设备输入或输出时,在预指令执行阶段,将选择的设备的设备码存入DMA的设备地址寄存器中---->这样在DMA启动的时候,就只有一台外部设备能够进行数据交互。
- 可见选择型是物理上多个设备同时连接,逻辑上仅能有一台设备实现交互。
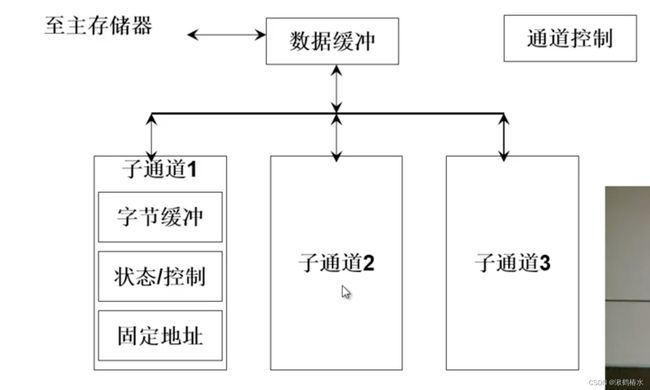
B、多路型(有多个DMA接口分别对应一个外部设备)
- 每个子通道就是一个DMA,所有的子通道组成一个通道,通道仅有一个数据通路和数据缓冲连接。
- 每个子通道都有自己的字节缓冲,当CPU执行到数据输入输出指令的时候,将同时需要输入或输出的多个设备地址号发送到不同的子通道上,每个子通道连接一个外部设备,启动后可以同时从多台外部设备中读入数据到对应的字节缓冲中(此时可以看作多个接口和设备同时工作)
- 当每个子通道数据准备完成后,将数据加入数据缓冲时,在主存看来还是仅面对一个通道来进行数据交换。
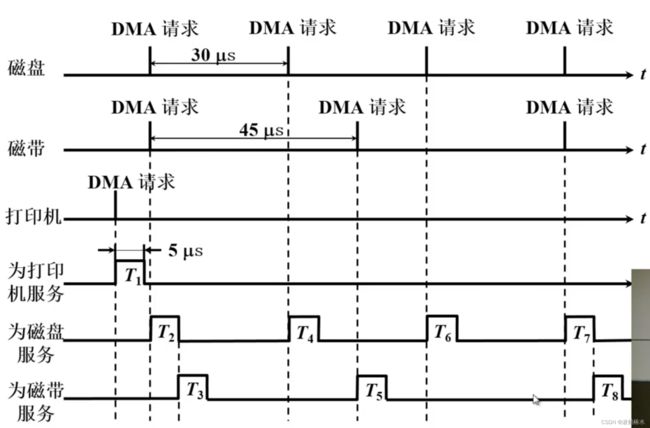
C、多路型的工作原理和时间空余
- 上图时同时连接了三台设备,三台设备每次占用总线指令发出时间间隔分别为30微秒,45微秒,150微秒。
- 任何一台设备占用总线后传输数据只需要5微秒。
- 现在三台设备中打印机率先发出总线和主存占用指令,占用主存和总线,用5微秒实现数据传输;然后稍等一会儿磁带和磁盘同时也请求总线占用,(遵循快速设备优先原则)先用5微秒响应磁盘的请求,然后再用5微秒处理磁带的数据传输。即使这样依然还剩余大量空余时间,这些时间没有被充分利用起来。
数字(计算机中的数据表示)
十四、计算机的运算方法
(一)无符号数和有符号数(原码方式表示)
A、无符号数
根据存储单元给定位数决定无符号数位数,如果是在寄存器中保存,那么寄存器的长度就反映了其能储存的数据范围,如给定寄存器位数为8位,那么数据范围就是0-255(8个0---8个1);
B、有符号数
我们需要一位用0/1来代表正号和负号,还需要一位来代表小数位置(小数没有固定硬件表示)
如: +1101 机器码就是 01101; -1101 机器码就是 11101;+0.1101 机器码就表示为 0 1101(紫色代表小数占用位); -0.1101 机器码表示就是 1 1101(紫色表示小数位); +1101就表示为 01101 这种情况,就是整数,小数位在最后。
C、原码表示法
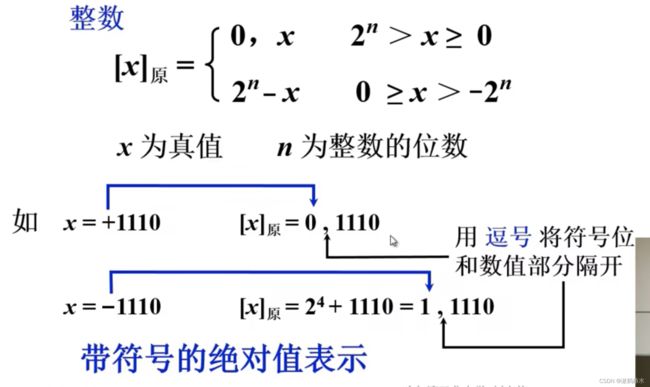
- 上面的方式都用最高位作为数的符号位,所以假如整数的二进制表示是n位,原值是x,则x的计算机表示[x],三者满足下列关系。
- 当x为正数时,增加符号位为0,其他位是x(真值)的绝对值,那么绝对值占用位的能够储存的数字范围为2^n>x>=0,区间为何是左开右闭,因为数字位的最高位(n)最大为1,所以永远无法达到2^n;
- 当x为负数时,增加符号为1,其他位为x,则计算机中表示为1 + x的绝对值,即1-x,因为符号位位1,所以如果符号为算入数据位则范围为[2^(n+1),2^(n+1)+2^n);
- 小数(绝对值小于1的数)
- 小数转换为原码,只需要将最开始的小数点前面的0作为符号位即可,小数位在符号位之后。
- 注意用原码表示法的话,0是有正负的,如果原码是0,000则为正零,1,0000则为负零(在数据位为4位时是如此)
C、原码表示法的优势和不足
优势:表示简单易懂;
不足:造成计算单元更复杂,比如同样是加法运算,就分为下面四种情况
| 加法运算可能情况 | 结果 |
|---|---|
| 两个正整数 | 加法 正数 |
| 一正一负 | 减法,根据绝对值情况而定,结果可正可负 |
| 两负 | 加法 负数 |
| 一负一正 | 减法 等同于第二种情况 |
这中情况的出现时因为加数有可能是负数导致的,那我们有没有一个数能够代替负数等价地去直接进行加法运算呢?
补码表示法解决了这个问题。
(二)无符号数和有符号数(补码方式表示)
A、补码的概念
- 由钟表引入
钟表只有12个小时,指针会不断旋转指向不同的值,这时如果我们这时时针指向6,那么我们要让6变为3有两种方法:
- 时针逆时针旋转3个小时
- 时针顺时针旋转9个小时
- 我们抽象概念知,12是模的话,一旦超过12就进行取模运算,得到结果。这样就实现了:6+9=15 和 6-3=3 最终结果就相等;我们把9和-3这样两个数其绝对值的和为12的数就称为互补数,通过这个技巧我们就能实现将正负数变为统一加法操作。
B、计算机实现补码
- 条件设置:计算机底层我们用四位结构来储存数据,我们在四位储存+1011,我们要让其变为0000也有两种方式:
- 1011-1011=0000;
- 1011+0101=0000;
- 为什么1011+ 0101 =0000?
- 1011+0101=10000,但是因为储存数据的位数只有四位,结果最高位的1超出四位,故数据位还是0000,所以就实现了1011 - 1011 = 1011 + 0101 =0的效果。
- 我们同样可以将-1011和1011这两个数看作互补数, 又因为1011 + 0101 = 10000,所以我们知道他们的模数为2^4=16,模数为16。
- 如此我们就可以实现将本来的正负数相加变为两个整数相加。如假设存储数据位还是4位,那么-101=+011 (mod=2^3),-0.1011=+1.0101(mod=2^1);
- 根据3我们可以知道下面几个结论:
- mod(模数)= 2^n(n为数据存储单元的位数);
- 要想得到一个数的互补数,需要每位取反加一,如+1011 ==》 -0100 ==〉 -0101,故+1011的互补数
C、发现规律,总结公式
+1011的补码是+1011 + 10000 = 11011,因为四个数据位,还是1011(正数的补码是其本身)。
-1011的补码是-1011 + 10000 = 0101(负数的补码是正数)
为了区分到底是负数还是正数的补码,我们在他们前面加上0或1来区分(0为正数的补码,1为负数的补码)
我们用2^5来计算两个数的补码: 100000 -1011 = 010101,因仅保留五位,故为1,0101;100000 + 1011 = 101011,因为是保留五位,故为0,1011。
可见最高位是1则是负数的补数,最高位是0则是正数的补数,故可得出如下公式:
整数补码公式:
小数补码公式及例子:
这里注意如果x为-1.0000时,其补码为1.0000,不能表示原码,因为1占用了符号位。
D、求补码的快捷方式
正整数:例如+1011 求其补码只需要将+变为0即可==》01011
负整数:例如-1011求其补码,先将-变为1,再将后面数值位取反后+1==〉 10101
原理:正常来讲:100000 - 1011 = 11111 + 1 - 1011 = 11111 - 1011 + 1;
正小数[0,1): 如 +0.1011,直接将+变为0作为符号位,小数点紧跟后面即为0.1011;
原理:10.0000 + 0.1011 = 10.1011 因位数仅5位,固为0.1011;
负小数(-1,0]:如 -0.1011 ,直接将-变为1作为符号位,小数点后取反加一,1.0101;
原理:10.0000 - 0.1011 =1.1111 -0.1011 + 1 = 1.0101;
E、补码和原码之间的转换
真值为负时,只需要将[x]补 保留符号位不变,其他取反加一,得到[x]原,例如0,1011(补码) ==》0,0101(原码)
真值为正时,原码与补码完全相同。
+0和-0的补码相同,原码不同。
原理:例如真值为+0.0000 补码为 0.0000,因为0.0000 + 10.0000 =10.0000(截去1,还是原值),负0同理。
(三)无符号数和有符号数(反码方式表示)
A、反码是什么?
反码获取只需要将原码符号位保留不变,正整数反码跟原码相同,负整数保留符号位不变,其他位取反(不用加1)
B、整数补码公式
因为不用加1,相当于模数减1。
C、小数补码公式
例子:-0.1010的反码:(2-2^(-4))-0.1010= 1.1111 - 0.1010 = 1.0101;(实际就是x的补码的最后一位减1)
D、+0和-0的原码和反码不一样
(四)三种表示方式总结
- 符号位和数值位在书写时用“,”或“.”隔开;
- 对于正数:其补码=原码=反码;
- 对于负数:其符号位为1。数值部分取反加1得到补码;数值部分不变得到原码;数值部分取反得到反码;
(五)原码、补码、反码表示范围(以8位数据为例)
取个别值分析:
- 补码10000000,其对应原码是100000000,一共九位,所以真值为2^8=128,又因为符号位为1,所以达到了用8位表达了-128的效果。
- 反码10000000,其对应原码为11111111,所以表示真值为-127。
(六)[y]补 和[-y]补的关系推导(例题)
设:[y]补 =y0.y1 y2 y3 y4....
情况一:[y]补 =0.y1 y2 y3 y4...
[y]补 =[y]原 ===>y = 0.y1 y2 y3 y4... ===> -y=-0.y1 y2 y3 y4 y5...
===>[-y]补=1.y1 y2 y3... + 2^n;( 字体表示取反)
情况二:[y]补 =1.y1 y2 y3 y4...
[y]原=[y]补 (排斥符号位)取反末位加1 = 1.y1 y2 y3... + 2^n
===> y=-(0.y1 y2 y3... + 2^n )==> -y=0.y1 y2 y3... + 2^n
===再次数值位取反===>[-y]补 = 0.y1 y2 y3 y4 y5... + 2^n
(七)无符号数和有符号数(移码表示方式)
A、为什么要出现移码?
- 因为真值转换为补码后,无法准确判断原值大小,所以要引入移码。
- 下表是一个补码和原值对照表
| 十进制 | 二进制 | 补码 |
| +21 | +10101 | 0,01011 |
| -21 | -10101 | 1,01011 |
| +31 | +11111 | 0,00001 |
| -31 | -11111 | 1,00001 |
0,01011 < 1,01011 (错误)因为+21 > -21; 0,00001 < 1,00001 因为+31 > -31;
B、移码的计算公式
- 不区分正负值,暂时不能处理小数的移码。n为数值位数,x为真值
- 举例:
- 真值x为+10100,那么[x]移=2^5 + 10100 = 1,10100;
- 真值x为-10100,那么[x]移 = 2^5 -10100 = 11111 - 10100 + 1 =01011 + 1 = 01100;前面加上一位符号位0,01100。
我们可以发现,正数的符号识别位为1,负数的识别位为0。这样就是解决了大小比较问题。
C、移码和补码的比较
| 十进制 二进制 | 补码 | 移码 |
| +21 +10101 | 0,01011 | 1,01011 |
| -21 -10101 | 1,01011 | 0,01011 |
| +31 +11111 | 0,00001 | 1,00001 |
| -31 -11111 | 1,00001 | 0,00001 |
- 我们发现补码与移码只差一个符号位(符号位相反)
D、移码和补码对照表
- 可以看到-100000的移码是将-100000向右移动了2^5位,用000000来表示(含一个符号位)
- 移码的特点:
- 移码为全零时,表示数据位表示的最小值
- +0和-0的移码相同都是 2^n + 0 = 2^n(n表示数据位数)
- 用移码表示浮点数的阶码非常容易判断浮点数阶码的大小(阶码马上会学到!)