InSAR 测量技术的基本原理
目录
- 1.单轨双天线横向模式
- 2.单轨双天线纵向模式
- 3.重复轨道单天线模式
- 4.InSAR 测量原理
![]()
本文由CSDN点云侠原创,爬虫网站请自重。
在InSAR的数据采集模式中,依据接收天线位置的几何关系的不同,可以将SAR干涉测量的工作模式分为:单轨双天线横向模式(XTI)、单轨双天线纵向模式(ATI)、重复轨道单天线模式(RTI)。
1.单轨双天线横向模式
此种模式需在一飞行平台上同时装置两个雷达天线系统,且两天线所构成的直线方向与飞行方向垂直。这种模式的时间基线为零,排除了不同时间所成像对之间地表变化的影响,影像间的配准也相对容易解决。但是空间基线B的选择余地很小,受到飞行平台的几何尺寸限制。该模式目前主要用于机载平台的干涉实验中。星载平台上装置双天线尚有一些技术问题难于克服。
2.单轨双天线纵向模式
这种模式也是在同一飞行平台上安装两个雷达天线系统,但是天线顺着平台的飞行方向一来安装,即两天线所构成的直线方向与飞行方向平行。这种模式可以用来精确测定地物的运动,常用于洋流制图、动目标监测以及定向波谱的测量。
3.重复轨道单天线模式
这种模式也是在同一飞行平台上安装两个雷达天线系统,但是天线顺着平台的飞行方向一来安装,即两天线所构成的直线方向与飞行方向平行。这种模式可以用来精确测定地物的运动,常用于洋流制图、动目标监测以及定向波谱的测量。

该法仅需在飞行平台上安装一个雷达天线系统,通过两次飞行对同一地区获取的影像来形成干涉,因此较适合于星载SAR传感器,因为此法需较精确的飞行路径,而卫星因运行于大气较少的轨道上,可稳定地沿轨道飞行,故较适合此种模式。
目前和今后一段时间内,利用星载SAR进行干涉测量均采用这种模式。为了克服时间基线的影响,采用双星串联飞行模式,可以获得时间间隔为一天的像对,目前较成功地是欧洲空间局所发射的ERS-1/ERS-2的两颗卫星在相同轨道经过同一地区前后仅相差一天。
4.InSAR 测量原理
合成孔径雷达干涉测量是利用卫星或飞机搭载的合成孔径雷达系统,通过两副天线同时观测(单轨模式),或两次近平行的观测(重复轨道模式),获取地面同一景观的复影像对。由于目标与两天线位置的几何关系,在复图像上产生了相位差,形成干涉条纹图。干涉条纹图中包含了斜距向上的点与两天线位置之差的精确信息。根据复雷达图像的相位差信息,利用传感器高度、雷达波长、波束视向及天线基线距之间的几何关系,通过成像处理、干涉数据处理和几何转换等来提取地面目标地形的三维信息。
InSAR干涉测量技术与其它遥感手段的最大不同在于它是基于相位的测量,因此,采用的数据是复数数据,即单视复数数据。

下面以星载重复轨道干涉测量为例来说明InSAR的基本原理,如图所示,是一个竖直方向上的剖面图, S 1 S_1 S1和 S 2 S_2 S2分别表示两幅天线的位置,它们之间的距离用基线距 B B B表示,基线与水平方向的夹角为 α \alpha α,基线可分解为沿斜距方向的分量 B / / B_{//} B//和垂直于斜距方向的分量 B ⊥ B_\perp B⊥, H i H_i Hi表示卫星 S i S_i Si的高度, θ i \theta_i θi表示卫星 S i S_i Si的视角, R i R_i Ri表示卫星到地面上一点 P P P的斜距,其中 i = 1 , 2 i=1,2 i=1,2,分别对应于卫星 S 1 S_1 S1和卫星 S 2 S_2 S2,地面上点的高程用 Z Z Z表示。另外令 R 2 = R 1 + Δ R R_2=R_1+\Delta R R2=R1+ΔR。
当两副天线所形成的复数影像精确配准后,对应象素值共扼相乘就形成干涉条纹图,即有:
复数影像1: u 1 = ∣ u 1 ∣ e j φ 1 u_1=|u_1|e^{j\varphi_1} u1=∣u1∣ejφ1
复数影像2: u 2 = ∣ u 2 ∣ e j φ 2 u_2=|u_2|e^{j\varphi_2} u2=∣u2∣ejφ2
干涉图:
u i n t = u 1 u 2 ∗ = ∣ u 1 ∣ ∣ u 2 ∣ e j ( φ 1 − φ 2 ) u_{int}=u_1u_2^{*}=|u_1||u_2|e^{j(\varphi_1-\varphi_2)} uint=u1u2∗=∣u1∣∣u2∣ej(φ1−φ2)
接收到的雷达信号的相位主要有两部分组成:一是往返路径确定的相位;一是由地面分辨率单元不同的散射特性造成的随机相位,用公式可表示为:
φ 1 = − 2 2 π λ R 1 + a r c { ε 1 } \varphi_1=-2\frac{2\pi}{\lambda}R_1+arc\{\varepsilon_1\} φ1=−2λ2πR1+arc{ε1}
φ 2 = − 2 2 π λ ( R 1 + Δ R ) + a r c { ε 2 } \varphi_2=-2\frac{2\pi}{\lambda}(R_1+\Delta R)+arc\{\varepsilon_2\} φ2=−2λ2π(R1+ΔR)+arc{ε2}
上式中右边第一项表示由于往返路径确定的相位, a r c { ε 1 } arc\{\varepsilon_1\} arc{ε1}和 a r c { ε 2 } arc\{\varepsilon_2\} arc{ε2}表示由地面分辨率单元不同的散射特性造成的随机相位,2为系数,表示两副天线都发射和接收信号,即反映往返双程的相位差。若是一副天线用于发射信号两幅天线同时接收信息,则系数应该为1,在干涉图中只反映单程的相位差。
一般地,我们假设在两次获取的影像中由于散射特性引起的随机相位贡献基本相同,则干涉图的相位就只与雷达信号传播的路径差有关,

根据上图的几何关系,
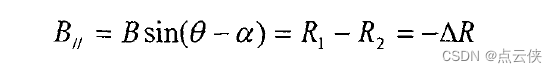

由干涉图得到的只是相位主值,还需要进行相位解缠才能得到真实的相位 Φ \Phi Φ。由上图知,在 Δ S 1 S 2 P \Delta S_1S_2P ΔS1S2P中由余弦定理可得:

对于星载雷达系统,通常 B < < R 1 B<
θ 1 = α − a r c s i n [ λ Φ 4 π B ] \theta_1=\alpha-arcsin[\frac{\lambda\Phi}{4\pi B}] θ1=α−arcsin[4πBλΦ]
Z = H 1 − R 1 c o s θ 1 Z=H_1-R_1cos\theta_1 Z=H1−R1cosθ1
其中, H 1 H_1 H1是雷达主传感器的高程, Z Z Z是地面点高程。由上述两式得出干涉相位差 Φ \Phi Φ与地面点高程 Z Z Z之间的数学关系。在已知天线位置(参数 H , B , α H,B,\alpha H,B,α)和雷达成像系统参数( θ \theta θ、 λ \lambda λ)等的条件下,就可以从中计算出地面的高程值 Z Z Z。