voronoi diagram(泰森多边形) 应用 - Empire Strikes Back

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

voronoi 图求解点击前往

题目链接：https://vjudge.net/problem/URAL-1520

题目大意

有一个城市，形状是圆形。

城市里有很多化工场。

现在想在每个化工厂里放置爆炸伤害半径相同的炸药。使得爆炸可以影响到整个城市。问最小半径是多少。

思考&分析

先求出每个化工厂所在voronoi区域的边。

判断边的交点是否在圆内。

voronoi区域的边与圆的交点，判断是否在voronoi区域的边区域内。

化工厂所在直径与圆的交点也有可能是最远点。

算法细节

1）判断区域与圆有交
可以求出区域所有顶点，判断有没有顶点在圆上或外面。

2）直线与圆求交

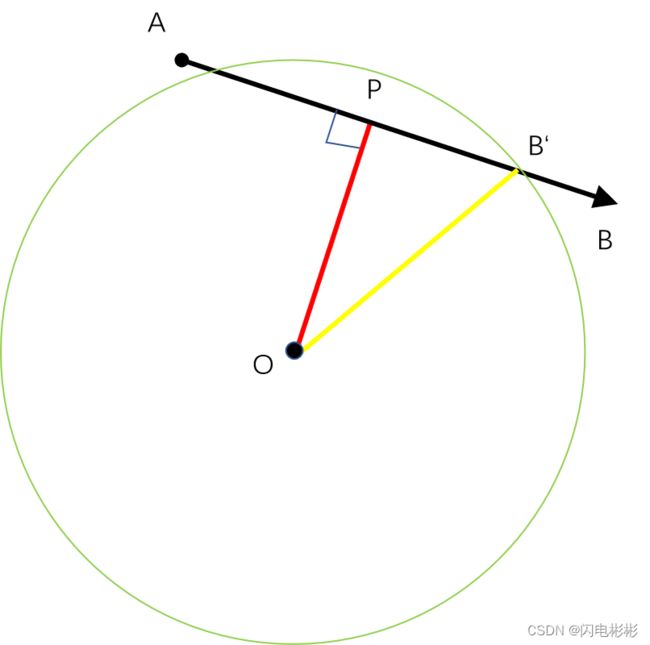
可以利用投影先求到P点，利用直角三角形可知PB’长度
从P点沿AB方向就可以得到B’坐标，同理，反向还有一个交点。

3）特殊情况
只有1个化工厂，取离圆边缘最远的距离。

只有2个化工厂或者所有工厂在一条线上时，不能进行三角化。

此时，对坐标进行排序，每两个最近的点取中垂线为分割线，也要考虑到直径与圆的交点是否为最远点。

算法过程

1个点，2个点，共线特殊处理

一般情况：

step 1 对边界点进行delaunay三角化
step 2 遍历每个边界点，收集邻边，并按照逆时针排序。
求解出每个邻边的中垂线，分别与边界和其他中垂线求交（邻近的中垂线才有交点）判断是否与圆有交集
step 3 求解与圆的交点，并判断交点是否在voronoi区域内。
step 4 直径与圆的交点并判断是否在voronoi区域内

代码

#include
#include
#include 
#include 
#include 
#include 
#include 


using namespace std;
const double EPS = 1e-8;

const int N = 1e6 + 10;
const int M = 1e6 + 10;

int cmp(double d) {
	if (abs(d) < EPS)return 0;
	if (d > 0)return 1;
	return -1;
}

class Point {
public:
	double x, y;
	int id;

	Point() {}
	Point(double a, double b) :x(a), y(b) {}
	Point(const Point& p) :x(p.x), y(p.y), id(p.id) {}

	void in() {
		scanf("%lf %lf", &x, &y);
	}
	void out() {
		printf("%f %f\n", x, y);
	}

	double dis() {
		return sqrt(x * x + y * y);
	}

	double dis2() {
		return x * x + y * y;
	}

	Point operator -() const {
		return Point(-x, -y);
	}

	Point operator -(const Point& p) const {
		return Point(x - p.x, y - p.y);
	}

	Point operator +(const Point& p) const {
		return Point(x + p.x, y + p.y);
	}
	Point operator *(double d)const {
		return Point(x * d, y * d);
	}

	Point operator /(double d)const {
		return Point(x / d, y / d);
	}


	void operator -=(Point& p) {
		x -= p.x;
		y -= p.y;
	}

	void operator +=(Point& p) {
		x += p.x;
		y += p.y;
	}
	void operator *=(double d) {
		x *= d;
		y *= d;
	}

	void operator /=(double d) {
		this ->operator*= (1 / d);
	}

	bool operator<(const Point& a) const {
		return x < a.x || (abs(x - a.x) < EPS && y < a.y);
	}

	bool operator==(const Point& a) const {
		return abs(x - a.x) < EPS && abs(y - a.y) < EPS;
	}
};

// 向量操作

double cross(const Point& a, const Point& b) {
	return a.x * b.y - a.y * b.x;
}

double dot(const Point& a, const Point& b) {
	return a.x * b.x + a.y * b.y;
}


class Point3D {
public:
	double x, y, z;

	Point3D() {}
	Point3D(double a, double b, double c) :x(a), y(b), z(c) {}
	Point3D(const Point3D& p) :x(p.x), y(p.y), z(p.z) {}

	double dis() {
		return sqrt(x * x + y * y + z * z);
	}

	double dis2() {
		return x * x + y * y + z * z;
	}

	Point3D operator -(const Point3D& p) const {
		return Point3D(x - p.x, y - p.y, z - p.z);
	}

	Point3D operator +(const Point3D& p) const {
		return Point3D(x + p.x, y + p.y, z + p.z);
	}
	Point3D operator *(double d)const {
		return Point3D(x * d, y * d, z * d);
	}

	Point3D operator /(double d)const {
		return Point3D(x / d, y / d, z / d);
	}


	void operator -=(Point3D& p) {
		x -= p.x;
		y -= p.y;
		z -= p.z;
	}

	void operator +=(Point3D& p) {
		x += p.x;
		y += p.y;
		z += p.z;
	}
	void operator *=(double d) {
		x *= d;
		y *= d;
		z *= d;
	}

	void operator /=(double d) {
		this ->operator*= (1 / d);
	}
};

// 向量操作
Point3D cross(const Point3D& a, const Point3D& b) {
	return Point3D(a.y * b.z - a.z * b.y, -a.x * b.z + a.z * b.x,
		a.x * b.y - a.y * b.x);
}

double dot(const Point3D& a, const Point3D& b) {
	return a.x * b.x + a.y * b.y + a.z * b.z;
}


class Line {
public:
	Point front, tail;
	Line() {}
	Line(Point a, Point b) :front(a), tail(b) {}
};

/*
0 不相交
1 相交
0 平行/重合
*/
int cross(const Line& a, const Line& b) {
	Point dir1 = a.front - a.tail;
	Point dir2 = b.front - b.tail;
	if (cmp(cross(dir1, dir2)) == 0) {
		return 0;
	}

	if (cmp(cross(a.front - b.tail, dir2)) * cmp(cross(a.tail - b.tail, dir2)) >= 0)return 0;
	if (cmp(cross(b.front - a.tail, dir1)) * cmp(cross(b.tail - a.tail, dir1)) >= 0)return 0;
	return 1;
}


int inCircle(Point p0, Point p1, Point p2, Point p3) {
	Point d1 = p1 - p0;
	Point d2 = p2 - p0;
	if (cross(d1, d2) < 0)return inCircle(p0, p2, p1, p3); // 保证平面法向向上

	// 构建映射点
	Point3D lift0(p0.x, p0.y, p0.dis2());
	Point3D lift1(p1.x, p1.y, p1.dis2());
	Point3D lift2(p2.x, p2.y, p2.dis2());
	Point3D lift3(p3.x, p3.y, p3.dis2());

	Point3D z1(lift1 - lift0), z2(lift2 - lift0);
	Point3D normal = cross(z1, z2); // 计算平面法向
	double project = dot(normal, lift3 - lift0); // 计算点到平面距离

	return cmp(project);
}



class EdgeDelaunay {
public:
	int id;
	std::list<EdgeDelaunay>::iterator c;
	EdgeDelaunay(int id = 0) { this->id = id; }
};

class Delaunay {
public:
	std::list<EdgeDelaunay> head[N];  // graph
	Point p[N];
	int n = 0;

	void init(int psize, Point ps[]) {
		this->n = psize;
		memcpy(this->p, ps, sizeof(Point) * n);
		std::sort(this->p, this->p + n);
		divide(0, n - 1);
	}

	void addEdge(int u, int v) {
		head[u].push_front(EdgeDelaunay(v));
		head[v].push_front(EdgeDelaunay(u));
		head[u].begin()->c = head[v].begin();
		head[v].begin()->c = head[u].begin();
	}

	void divide(int l, int r) {
		if (r - l <= 1) {  // #point <= 2
			for (int i = l; i <= r; i++)
				for (int j = i + 1; j <= r; j++) addEdge(i, j);
			return;
		}
		int mid = (l + r) / 2;
		divide(l, mid);
		divide(mid + 1, r);

		std::list<EdgeDelaunay>::iterator it;
		int nowl = l, nowr = r;

		for (int update = 1; update;) {
			// 查找左边最低线位置
			update = 0;
			Point ptL = p[nowl], ptR = p[nowr];
			for (it = head[nowl].begin(); it != head[nowl].end(); it++) {
				Point t = p[it->id];
				double v = cross(ptL - ptR, t - ptR);
				if (cmp(v) > 0 || (cmp(v) == 0 && (t - ptR).dis() < (ptL - ptR).dis())) {
					nowl = it->id, update = 1;
					break;
				}
			}
			if (update) continue;
			// 查找右边最低线位置
			for (it = head[nowr].begin(); it != head[nowr].end(); it++) {
				Point t = p[it->id];
				double v = cross(ptR - ptL, t - ptL);
				if (cmp(v) < 0 || (cmp(v) == 0 && (t - ptL).dis() < (ptL - ptR).dis())) {
					nowr = it->id, update = 1;
					break;
				}
			}
		}

		addEdge(nowl, nowr);  // 添加基线

		for (; true;) {
			Point ptL = p[nowl], ptR = p[nowr];
			int ch = -1, side = 0;
			for (it = head[nowl].begin(); it != head[nowl].end(); it++) {
				if (cmp(cross(ptR - ptL, p[it->id] - ptL)) <= 0)continue; // 判断夹角是否小于180
				if (ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0) {
					ch = it->id, side = -1;
				}
			}
			for (it = head[nowr].begin(); it != head[nowr].end(); it++) {
				if (cmp(cross(p[it->id] - ptR, ptL - ptR)) <= 0) continue;// 判断夹角是否小于180
				if (ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0) {
					ch = it->id, side = 1;
				}
			}
			if (ch == -1) break;  // 所有线已经加完
			if (side == -1) {
				for (it = head[nowl].begin(); it != head[nowl].end();) {
					// 判断是否相交，边缘不算相交
					if (cross(Line(ptL, p[it->id]), Line(ptR, p[ch]))) {
						head[it->id].erase(it->c);
						head[nowl].erase(it++);
					}
					else {
						it++;
					}
				}
				nowl = ch;
				addEdge(nowl, nowr);
			}
			else {
				for (it = head[nowr].begin(); it != head[nowr].end();) {
					// 判断是否相交，边缘不算相交
					if (cross(Line(ptR, p[it->id]), Line(ptL, p[ch]))) {
						head[it->id].erase(it->c);
						head[nowr].erase(it++);
					}
					else {
						it++;
					}
				}
				nowr = ch;
				addEdge(nowl, nowr);
			}
		}
	}

	std::vector<std::pair<int, int> > getEdge() {
		std::vector<std::pair<int, int> > ret;
		ret.reserve(n);
		std::list<EdgeDelaunay>::iterator it;
		for (int i = 0; i < n; i++) {
			for (it = head[i].begin(); it != head[i].end(); it++) {
				ret.push_back(std::make_pair(p[i].id, p[it->id].id));
			}
		}
		return ret;
	}
};

/*
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
线段1 上1点用 p' = p+t*r (0<=t<=1)
线段2 上1点用 q' = q+u*s (0<=u<=1)
让两式相等求交点 p+t*r = q+u*s
两边都叉乘s
(p+t*r)Xs = (q+u*s)Xs
pXs + t*rXs = qXs
t = (q-p)Xs/(rXs)
同理，
u = (p-q)Xr/(sXr) -> u = (q-p)Xr/(rXs)

以下分4种情况：
1. 共线，sXr==0 && (q-p)Xr==0, 计算 (q-p)在r上的投影在r长度上的占比t0，
计算(q+s-p)在r上的投影在r长度上的占比t1，查看[t0, t1]是否与范围[0，1]有交集。
如果t0>t1, 则比较[t1, t0]是否与范围[0，1]有交集。
t0 = (q-p)*r/(r*r)
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 平行sXr==0 && (q-p)Xr!=0
3. 0<=u<=1 && 0<=t<=1 有交点
4. 其他u, t不在0到范围内，没有交点。
*/
pair<double, double> intersection(const Point& q, const Point& s, const Point& p, const Point& r) {
	// 计算 (q-p)Xr
	auto qpr = cross(q - p, r);
	auto qps = cross(q - p, s);

	auto rXs = cross(r, s);
	if (cmp(rXs) == 0)return { -1, -1 }; // 平行或共线
	// 求解t, u
	// t = (q-p)Xs/(rXs)
	auto t = qps / rXs;

	// u = (q-p)Xr/(rXs)
	auto u = qpr / rXs;

	return { u, t };
}


Point oiPs[N];
Delaunay de;
Point lowPoint;
int ind[M];
Point tmpPs[N]; // 存储与边界的交点
int cakeSize[N];

vector<Point> insectCircle(const Point& A, const Point& dir, double r) {
	vector<Point> ans;
	Point P = A + dir * dot(dir, -A);
	double op = abs(cross(dir, A));
	if (cmp(op - r) > 0)return ans;

	double Pb = sqrt(r * r - op * op);
	if (cmp(Pb) == 0) ans.push_back(P);
	else {
		ans.push_back(P + dir * Pb);
		ans.push_back(P - dir * Pb);
	}

	return ans;
}

// 按照极坐标排序
bool sortcmp(int i, int j) {
	Point pi = oiPs[i] - lowPoint;
	Point pj = oiPs[j] - lowPoint;

	// 在上下半区不同侧，上半区优先
	if (cmp(pi.y * pj.y) < 0) return pi.y > pj.y;
	pi /= pi.dis();
	pj /= pj.dis();
	// 有一条为1，0, x大的优化
	if (cmp(pi.x - 1) == 0 || 0 == cmp(pj.x - 1)) return pi.x > pj.x;

	double d = cmp(cross(pi, pj)); // 同侧判断是否逆时针旋转
	return d > 0;
}

bool oneLine(int n) {
	if (n < 3)return true;
	for (int i = 2; i < n; ++i) {
		if (cmp(cross(oiPs[1] - oiPs[0], oiPs[i] - oiPs[0])) != 0) return false;
	}

	return true;
}

void  solve() {
	int n, r;

	scanf("%d%d", &n, &r);
	int a, b;
	for (int i = 0; i < n; ++i) {
		//scanf("%lf%lf", &oiPs[i].x, &oiPs[i].y);
		scanf("%d%d", &a, &b);
		oiPs[i].x = a;
		oiPs[i].y = b;
		oiPs[i].id = i;
	}

	if (n == 1) {
		printf("%.10f\n", r+oiPs[0].dis());
		return;
	}

	double maxRadius = 0;

	// 判断是否共线
	if (oneLine(n)) {
		// 排成一条线每两点垂直平分线为分隔。
		sort(oiPs, oiPs + n);
		for (int i = 0; i < n; ++i) {
			vector<pair<Point, Point>> midLines;
			if (i) {
				Point mid = (oiPs[i] + oiPs[i-1]) / 2;
				Point dir = oiPs[i] - oiPs[i - 1];
				dir = { -dir.y, dir.x }; // 旋转90度
				dir /= dir.dis();
				midLines.push_back({ mid, dir });
			}

			if (i + 1 < n) {
				Point mid = (oiPs[i] + oiPs[i + 1]) / 2;
				Point dir = oiPs[i] - oiPs[i + 1];
				dir = { -dir.y, dir.x }; // 旋转90度
				dir /= dir.dis();
				midLines.push_back({ mid, dir });
			}


			int k = 0;
			// 求直径与圆的交点
			if (oiPs[i].dis() > EPS) {
				tmpPs[k++] = oiPs[i] / oiPs[i].dis() * r;
				tmpPs[k] = -tmpPs[k - 1];
				k++;
			}

			for (auto& midLine : midLines) {
				// 求与圆的交点
				auto cirs=insectCircle(midLine.first, midLine.second, r);

				for (auto& c : cirs) {
					maxRadius = max(maxRadius, (c - oiPs[i]).dis());
				}
				// 排除不在区域内的直径交点
				for (int j = 0; j < k; ++j) {
					// 判断点是否与Lowpoint 在同一半平面内
					if (cmp(cross(oiPs[i] - midLine.first, midLine.second) * cross(midLine.second, tmpPs[j] - midLine.first)) > 0) {
						swap(tmpPs[k - 1], tmpPs[j]);
						k--;
						j--;
						continue;
					}
				}
			}

			// 取直径交点最大值
			for (int j = 0; j < k; ++j) {
				maxRadius = max(maxRadius, (tmpPs[j] - oiPs[i]).dis());
			}
		}

		printf("%.10f\n", maxRadius);
		return;
	}

	oiPs[n] = oiPs[0];

	de.init(n, oiPs);
	auto oiedges = de.getEdge();
	vector<vector<int>> link(n, vector<int>());
	for (auto oie : oiedges) {
		link[oie.first].push_back(oie.second);
	}

	for (int i = 0; i < n; ++i) {
		// 遍历每个边界点，收集邻边，并按照逆时针排序。
		int len = 0;
		for (auto to : link[i]) {
			ind[len++] = to;
		}

		lowPoint = oiPs[i];
		sort(ind, ind + len, sortcmp);
		ind[len] = ind[0];// 添加循环优化

		int k = 0;
		// 求voronoi 边界之间交点
		for (int i = 0; i < len; ++i) {
			Point mid = (lowPoint + oiPs[ind[i]]) / 2;
			Point dir = oiPs[ind[i]] - lowPoint;
			dir = { -dir.y, dir.x }; // 旋转90度

			Point mid2 = (lowPoint + oiPs[ind[i + 1]]) / 2;
			Point dir2 = oiPs[ind[i + 1]] - lowPoint;
			dir2 = { -dir2.y, dir2.x }; // 旋转90度

			// 判断是否为都边界（夹角不能大于180）
			if (cmp(cross(dir, dir2)) > 0) {
				// 求交点 
				auto pr = intersection(mid, dir, mid2, dir2);

				Point ablePoint = mid2 + dir2 * pr.second;
				if (cmp(ablePoint.dis() - r) <= 0) maxRadius = max(maxRadius, (ablePoint - lowPoint).dis());
			}

			// 求直径与圆的交点
			if (lowPoint.dis() > EPS) {
				tmpPs[k++] = lowPoint / lowPoint.dis() * r;
				tmpPs[k] = -tmpPs[k - 1];
				k++;
			}
			dir /= dir.dis();
			// 求与圆的交点
			auto cirs = insectCircle(mid, dir, r);

			for (auto& c : cirs) {
				tmpPs[k++] = c;
			}
		}

		// 排除无效交点
		for (int i = 0; i < len; ++i) {
			Point mid = (lowPoint + oiPs[ind[i]]) / 2;
			Point dir = oiPs[ind[i]] - lowPoint;
			dir = { -dir.y, dir.x }; // 旋转90度
			for (int j = 0; j < k; ++j) {
				// 判断点是否与Lowpoint 在同一半平面内
				if (cmp(cross(lowPoint - mid, dir) * cross(dir, tmpPs[j] - mid)) > 0) {
					swap(tmpPs[k - 1], tmpPs[j]);
					k--;
					j--;
					continue;
				}
			}
		}
		for (int j = 0; j < k; ++j) {
			maxRadius = max(maxRadius, (tmpPs[j] - lowPoint).dis());
		}
	}

	printf("%.10f\n", maxRadius);
	//printf("%d\n", maxSize);
	//printf("%.10f\n", seat.dis());
}



int main() {
	solve();
	return 0;

}

/*
5 10
0 0 
1 0 
0 1 
0 -1
-1 0

5 10
-1 0
0 0
-1 1
-1 -1
-2 0

5 10
0 0
10 0
0 10
0 -10
-10 0


10 3
1 -1 100
2 2 200
-2.5 -2.56 1

10 5
0.2 0 100
1 0 1
2 0 2
3 0 1
4 0 4

10 5
9.89 0 100
1 0 1
2 0 2
3 0 1
4 0 4

10 2
10 0 100
1 0 1


2 5
2 0
-2 0

2 5
2 -2
-2 -2

6 10
1 0
-1 0
2 0
-2 0
3 0
-3 0

6 10
1 -1
-1 -1
2 -1
-2 -1
3 -1
-3 -1

6 10
-4 -1
-1 -1
-5 -1
-2 -1
-6 -1
-3 -1

*/

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。创作不易，帮忙点击公众号的链接。